Fakultät
In diesem Artikel geht es um die Fakultät im Sinne der Mathematik. Zunächst wird eine Definition der Fakultät (Mathe) gegeben und zugehörige Rechenregeln werden erklärt. Im Anschluss wird anhand eines Beispiels erläutert, wie sich die Fakultät berechnen lässt.
Lesen ist dir zu altmodisch? Finden wir auch! Deshalb haben wir hier ein Video für dich, welches dir sofort alle wichtigen Infos vermittelt.
Inhaltsübersicht
Fakultät Definition
Die Fakultät im Sinne der Mathematik bezeichnet eine Funktion aus der Kombinatorik. Die Schreibweise ist n! (gesprochen: „n Fakultät“ ). Mit der Fakultät, welche auch als Faktorielle (Österreich) bezeichnet wird, lässt sich bestimmen, wie viele Möglichkeiten es gibt n Objekte einer Menge anzuordnen (Anzahl Permutationen ).
Fakultät Formel
„n!“ lässt sich berechnen, indem man alle natürlichen Zahlen (also ganzzahlige positive Ziffern) von 1 bis n miteinander multipliziert:
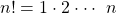
„n“ steht hierbei für die Zahl von der die Fakultät gebildet werden soll.
Diese wird in der Mathematik üblicherweise durch ein Ausrufezeichen dargestellt.
Die alternative Produkt-Schreibweise lautet:
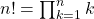
Eine dritte Möglichkeit, diese zu beschreiben, ist die rekursive also rückwärts gewandte Schreibweise:
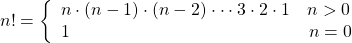
3 Fakultät
Die Fakultät von 3 ergibt sich, indem man alle ganzzahligen Zahlen von 1 bis 3 miteinander multipliziert. Ziel ist es also, das Produkt von 1, 2 und 3 zu bilden. Formal aufgeschrieben sieht dies wie folgt aus:
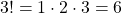
5 Fakultät
„n!“ von 5 lässt sich identisch berechnen:
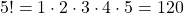
7 Fakultät
„n!“ für 7 ergibt sich äquivalent:

Fakultät Taschenrechner
Das Prinzip der Berechnung sollte anhand der vorherigen einfachen Beispiele klar geworden sein. Für größere Zahlen ist die Berechnung per Hand sehr umfangreich und im Kopf kaum noch möglich. Man verwendet deshalb am besten einen Fakultät Rechner oder einen handelsüblichen wissenschaftlichen Taschenrechner. Dazu muss in der Regel nur die gewünschte Zahl und das Ausrufezeichen (x!) in den Taschenrechner eingegeben werden und das gesuchte Ergebnis erscheint.
Fakultät Beispiel
In einem Supermarktregal stehen 6 verschiedene Arten Spirituosen in einer Reihe. Um den Kunden optische Abwechslung zu bieten, ändert der Supermarkt jede Woche die Anordnung der alkoholischen Getränke. Die Leitung des Supermarktes fragt sich nun, wie lange die Spirituosen neu angeordnet werden können, ohne dass eine Kombination doppelt vorkommt.
Um diese Fragestellung zu beantworten, eignet sich die Formel der Fakultät. Die Antwort lässt sich berechnen indem man n! von 6 bestimmt:
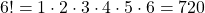
Es gibt also 720 Varianten die Flaschen umzustellen. Dies bedeutet, dass man die Flaschen 720 Wochen – also  14 Jahre – neu anordnen kann, ohne dass sich eine Formation wiederholt.
14 Jahre – neu anordnen kann, ohne dass sich eine Formation wiederholt.
Null Fakultät
Die 0 Fakultät nimmt per Definition immer den Wert 1 an.
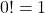
Die Fakultät von 0 ist damit ein Sonderfall in der Mathematik, da sie ein Produkt mit 0 Faktoren ist. Diesem Sonderfall des leeren Produkts wird grundsätzlich immer der Wert 1 zugewiesen.
Fakultät Kürzen
Da es sich bei der Fakultät um eine multiplikative Verknüpfung handelt, kann diese nach den klassischen Regeln zum Kürzen vereinfacht werden.
Beispiel:
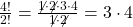
Augenscheinlich kann es in Bezug auf das Kürzen manchmal sinnvoller sein, den Bruch mit n! stehen zu lassen, anstatt diesen zu kürzen. Am Ergebnis ändert sich durch das Kürzen natürlich nichts.
Fakultät Mathe Anwendungen
Die Fakultät kann im Rahmen des Binomialkoeffizienten genutzt werden, um zu bestimmen, wie viele Möglichkeiten es gibt k Elemente einer Menge n in einem Zufallsexperiment mit „Ziehen ohne zurücklegen ohne Reihenfolge “ anzuordnen. Die Bestimmung kann mit folgender Formel vorgenommen werden:
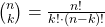
Neben der Anwendung in der Kombinatorik gibt es vielfältige weitere Anwendungsmöglichkeiten für den Binomialkoeffizienten. In unserem Video erfährst du mehr darüber!
