Performancemaße – Gespaltene Soll- und Habenzinsen
Die Performancemaße hast du eigentlich verstanden, aber die unterschiedlichen Zinssätze für Geldanlage und Geldaufnahme bereiten dir noch Probleme?
Das ändern wir jetzt!
Inhaltsübersicht
Auswirkungen von Soll- und Habenzinsen
In den vorherigen Videos haben wir uns die verschiedenen Performancemaße unter der Annahme gleicher Soll- und Habenzinsen angeschaut. Wie du dir vielleicht schon gedacht, ist das in der Realität
eher selten, da du meistens höhere Zinsen zur Geldaufnahme bezahlen musst als du bei Geldanlage bekommst.
Bei der Differenzrendite und der RAP ging es ja für die Vergleichbarkeit der Renditen immer darum, die Performance einer Anlage auf das Risiko der anderen Anlage zu Hebeln.
Dabei kommt es auf das Risiko an, mit dem die Anlage verbunden ist. Entweder wird das Hebeln durch Kreditaufnahme und Anlage des aufgenommenen Geldes in den Fond oder das Marktportfolio vorgenommen. Oder es werden Fondsanteile verkauft und der Erlös zu RF angelegt.
Schauen wir uns jetzt mal an, welche Auswirkungen unterschiedliche Soll- und Habenzinsen auf dieses Hebeln haben.
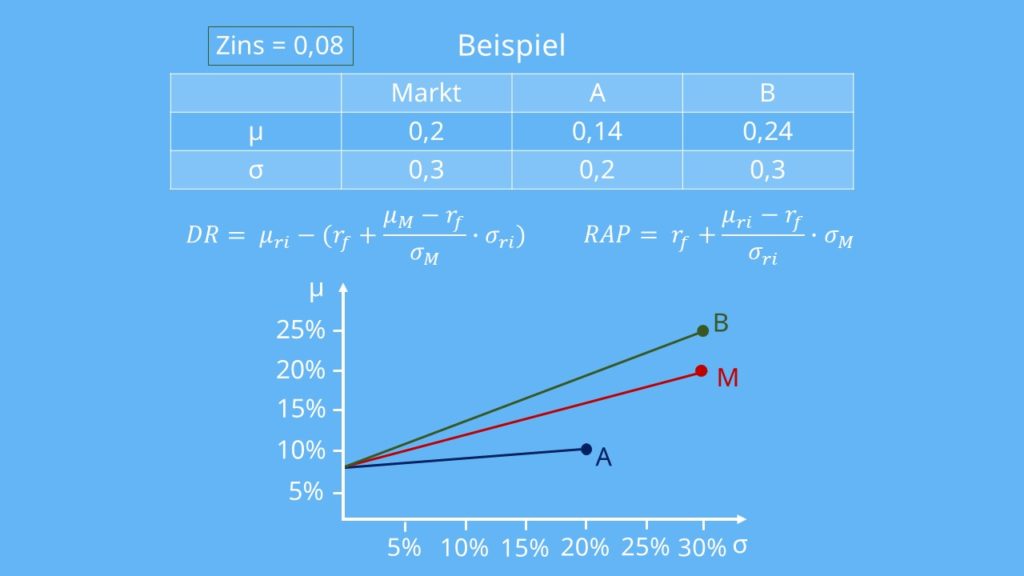
Gegeben ist eine Tabelle mit Müh und Sigma eines Marktes und der Fonds A und B.
Zeichnest du das in ein Koordinatensystem mit Müh und Sigma an den Achsen ein, sieht das dann so aus:
Beispielrechnung
Um die Auswirkungen besser vergleichen zu können, bestimmen wir als erstes jeweils die Differenzrendite und die RAP für Fonds A und Fonds B für den einheitlichen Soll- und Habenzins 0,08.
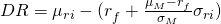
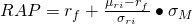
Die RAP für Fonds A ist also:
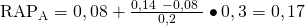
Und für Fonds B:
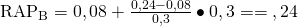
Die Differenzrendite beträgt -0,02 für Fonds A und 0,04 für Fonds B.
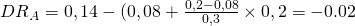
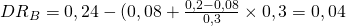
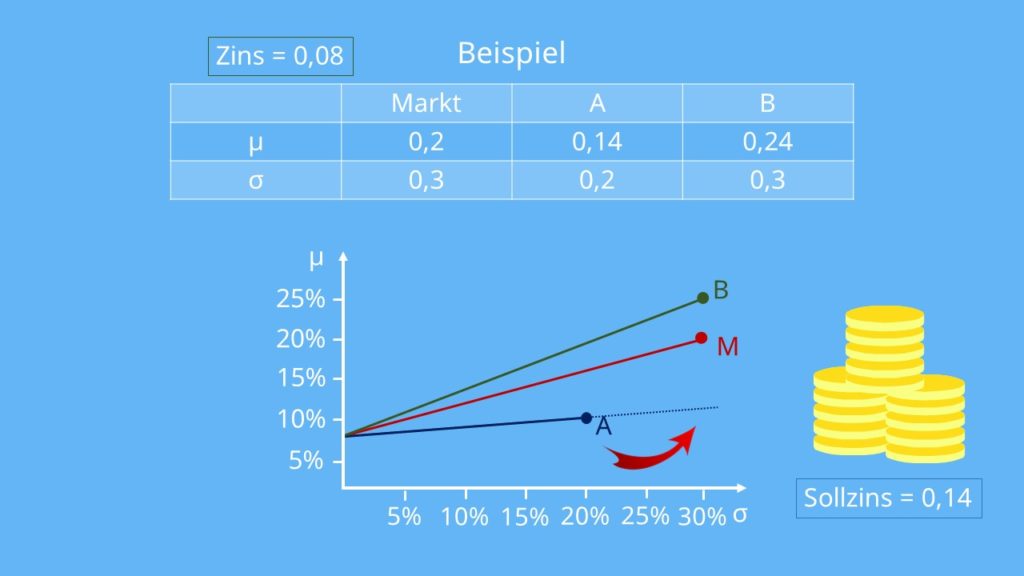
Soweit ist das ja alles noch bekannt. Jetzt wollen wir uns anschauen was passiert, wenn sich der Sollzinssatz verändert. Dazu betrachten wir nochmal die Zeichnung. Wenn du die RAP von A bestimmen willst, machst du ja nichts anderes, als den Fonds auf das Marktrisiko zu hebeln. Da der Markt ein höheres Risiko als der Fonds A hat, geht das nur über Geldaufnahme zum Sollzinssatz von jetzt 14 % und Investition des aufgenommenen Kapitals in den Fonds A.
Dementsprechend verändert sich die Rechnung zur RAP im Vergleich zu vorhin. Anstatt 0,08 müssen wir jetzt jeweils 0,14 als risikofreien Zins einsetzen.
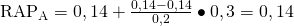
Dementsprechend ergibt sich eine RAP von 0,14 für A.
Jetzt fragst du dich bestimmt, wie das bei Fonds B aussieht. Da dieser von Anfang an die selbe Standardabweichung besitzt wie der Markt, musst du beim Hebeln weder Geld aufnehmen noch zusätzlich anlegen. Die RAP bleibt somit identisch.
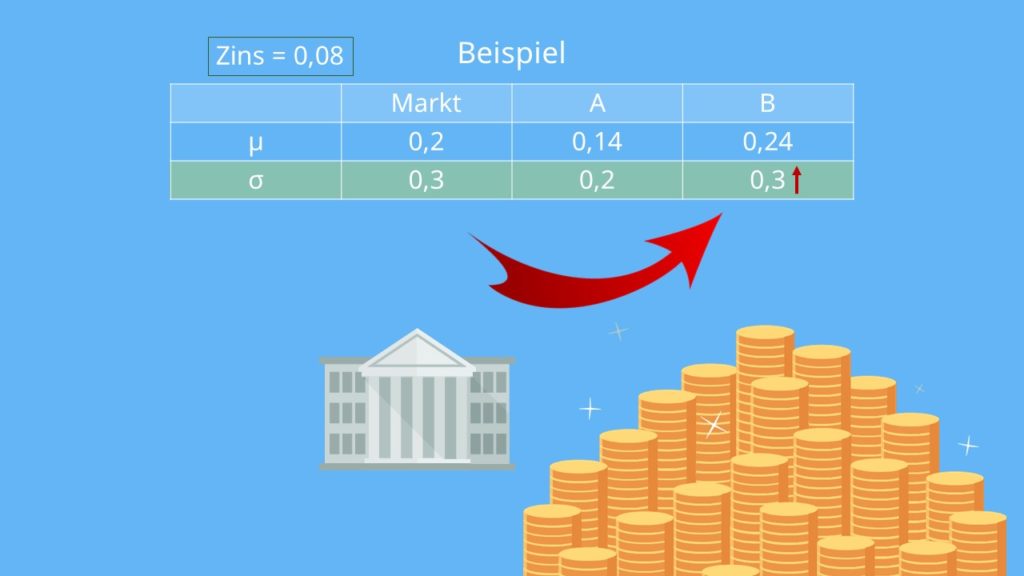
Würde der Fonds eine höhere Standardabweichung besitzen, würde sich trotzdem nichts an der Berechnung der RAP verändern, da du dann zur Risikoangleichung Geld aus dem Fonds herausnehmen und in die risikofreie Anlage investieren müsstest. Der Habenzins ist ja aber weiterhin 0,08, wie zuvor.
Änderung der Differenzrendite
Soweit so gut. Schauen wir uns nun an, was bei der Differenzrendite passiert. Bei dieser wird der Markt auf das Risiko der jeweiligen Anlage gebracht. Dementsprechend verändert sich in unserem Beispiel nichts, da Du für Fonds A Geld zu Habenzins anlegen musst und für Fonds B weiterhin das selbe Risikoniveau wie zuvor vorliegt.
Anders wäre das, wenn Fonds B ein größeres Risiko als der Markt hätte, dann könntest du den Markt nur über Aufnahme von Fremdkapital und Anlage in den Markt auf das Risiko von Fonds B hebeln.
Wie du siehst, kannst du bei gespaltenen Zinssätzen nicht pauschal sagen, wie sich die Performancemaße verändern, ohne mehr über das Risiko der einzelnen Anlagen zu wissen.
Um nicht durcheinander zu kommen, kannst du dir einfach immer kurz die Lage der Anlagen im Koordinatensystem einzeichnen und nachvollziehen, was wohin gehebelt wird.