Erste Irrelevanzthese nach Modigliani/ Miller
Wer sind Modigliani und Miller und was haben sie mit der Kapitalstruktur zu tun?
All das beantworten wir dir hier!
Inhaltsübersicht
Einfluss des Verschuldungsgrades auf Kapitalkosten
Bei der Irrelevanzthese von Modigliani/Miller geht es um den Einfluss des Verschuldungsgrades auf die Kapitalkosten eines Unternehmens. Die Herren Modigliani/Miller bewiesen, dass unter bestimmten Bedingungen weder die Kapitalstruktur noch die Dividendenpolitik eines Unternehmens einen Einfluss auf den Unternehmenswert haben.
Die grundlegenden Annahmen dabei sind, dass ein vollkommener Kapitalmarkt vorliegt und keine Steuern, Transaktionskosten und asymmetrische Information existieren. Außerdem findet eine kapitalmarktorientierte Bewertung von Eigenkapital und Fremdkapital auf Grundlage der Marktwerte statt.
Ist die Kapitalstruktur gegeben, bestimmt diese die Aufteilung der Überschüsse aus einer Periode an Eigenkapital und Fremdkapital. Unter der Voraussetzung eines vollkommenen Kapitalmarkts beeinflusst die Kapitalstruktur den Gesamtwert aus Eigenkapital und Fremdkapital eines Unternehmens nicht. In der Summe fließen den beiden Positionen immer die gleichen Periodenüberschüsse zu.
Law of one price
Wichtig für die Irrelevanzthese ist zudem, dass „the law of one price“ gilt. Also, dass gleiche Finanztitel auf allen Märkten denselben Preis haben sollten. „Gleich“ bedeutet in diesem Fall, dass der Überschuss sowie das Geschäfts- und Kapitalstrukturrisiko gleich sind.
Im Gegensatz zur traditionellen These aus dem vorherigen Video, besagt die These von Modigliani/Miller, dass zwei Unternehmen, die sich nur in Bezug auf das Kapitalstrukturrisiko unterscheiden, im Marktgleichgewicht gleiche Gesamtunternehmenswerte aufweisen.
Dieses Theorem wird durch einen Arbitragebeweis gestützt. Dieser zeigt: Wenn Marktwertunterschiede zwischen zwei vergleichbaren Unternehmen mit unterschiedlicher Verschuldung vorliegen, dann werden diese durch Arbitrageoperationen von rationalen Investoren ausgeglichen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispielaufgabe
Schauen wir uns diesen Arbitragebeweis mal anhand einer Beispielaufgabe an.
Gegeben sind die zwei Unternehmen A und B, die sich in derselben Risikoklasse befinden. Ein Anleger besitzt eine Eigenkapital-Position von 8.000 Euro an Unternehmen B und somit 50 Prozent an den jährlichen Überschüssen von B. In der Tabelle sind die erwarteten Bruttoperiodenüberschüsse vor Fremdkapital-Zinsabzug, das risikolose Fremdkapital, dessen Zinssatz und der Marktwert des Eigenkapitals aufgeführt.
Die Ausgangsfrage ist jetzt, ob ein Gleichgewicht besteht und die beiden Unternehmen somit gleich viel wert sind. GK Null von A ist 12.000 plus 6.000 gleich 18.000 und somit kleiner als GK Null von B mit 16.000 plus 4.000 gleich 20.000. Sie sind somit nicht gleich viel wert und es besteht eine Arbitragemöglichkeit; also eine risikolose Möglichkeit für den Anteilseigner durch Kauf und Verkauf von Unternehmensanteilen Gewinne zu erzielen.
Um später kontrollieren zu können, ob sich seine Position verändert hat, schauen wir uns zunächst die Ausgangssituation vor der Transaktion an. Durch seine Eigenkapital-Position besitzt der Anleger 50 Prozent an den jährlichen Überschüssen von B, die um die Zinsen reduziert werden.Also
 .
.
Ihm fließen also jährlich Zahlungen in Höhe von 800 Euro zu.
So viel zur Ausgangssituation. Kommen wir zu den Arbitragetransaktionen.
Arbitragetransaktionen
Im ersten Schritt verkauft der Anleger seine 50 Prozent Anteile an Unternehmen B am Markt. Er erhält dafür
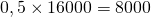
Der Anleger nimmt im zweiten Schritt einen Kredit in Höhe von 50 Prozent des Fremdkapitals von B auf. Also

Im dritten Schritt kauft der Anleger 50 Prozent des Eigenkapitals und Fremdkapitals von Unternehmen A. Also

Sein Arbitragegewinn aus den Transaktionen per Heute ist also:
Um zu überprüfen, ob die neue Situation des Anlegers der vorherigen entspricht, überprüfen wir den neuen Zustand anhand einer Kontrollrechnung.
Dem Anleger stehen jedes Jahr 50 Prozent-Anteile der Periodenüberschüsse von A minus Fremdkapital-Zins zu, also:

Der Anleger besitzt zudem 50 Prozent Anteil an den Fremdkapital-Zahlungen von A:

Außerdem zahlt er Zinsen auf den Kredit von Unternehmen B in Höhe von 50 Prozent des Fremdkapitals:

Insgesamt setzen sich die Zahlungen, die dem Anleger nach der Arbitragetransaktion zufließen, aus 700 plus 300 plus, in Klammern, minus 200 gleich 800 zusammen. Er erhält also denselben Betrag wie vor der Transaktion.
Fazit
Die Konsequenz daraus ist, dass das unterbewertete Unternehmen A an Wert zulegt, während das überbewertete B Unternehmen an Wert verliert, bis sie im Gleichgewicht wieder identische Unternehmenswerte aufweisen. Selbst wenn zwei Unternehmen einer Risikoklasse in der Ausganssituation einen unterschiedlichen Marktwert haben, sorgt die Arbitragemöglichkeit dafür, dass sich die Marktwerte anpassen und wieder ein Gleichgewicht entsteht.
Zusammengefasst kann man also sagen: Die Aktien des relativ hoch angesetzten Unternehmens werden verkauft, die Aktien des Unternehmens mit relativ niedrigem Marktwert werden gekauft. Je nach Situation wird dann vom Anleger zusätzlich ein Kredit gegeben oder aufgenommen.
Wie in der Rechnung zu sehen, spielt es für den Marktwert eines Unternehmens also keine Rolle, welche Kapitalstruktur es aufweist. Genau davon geht die erste These von Modigliani/Miller aus. Der Marktwert des Gesamtkapitals ist unabhängig von der Kapitalstruktur und wird durch Diskontierung der erwarteten Periodenüberschüsse mit den risikoadäquaten Kapitalkosten der jeweiligen Risikoklasse des Unternehmens berechnet. Also:

Jetzt weißt du schon Mal, was Modigliani und Miller mit der Finanzwelt zu tun haben. Das vorgestellte Theorem beinhaltet allerdings noch weitere Aspekte. Also: einfach dranbleiben!




