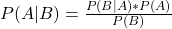Satz von Bayes
Dieser Artikel erklärt wie und wann man den Satz von Bayes anwenden kann, um Aufgaben zur bedingten Wahrscheilichkeit mit der Formel von Bayes zu lösen .
Das sind dir zu viele Sätze? Alles, was du zur Bayes Formel wissen musst, erfährst du auch in unserem Video , ohne auch nur einen einzigen Satz lesen zu müssen!
Inhaltsübersicht
Bayes Theorem
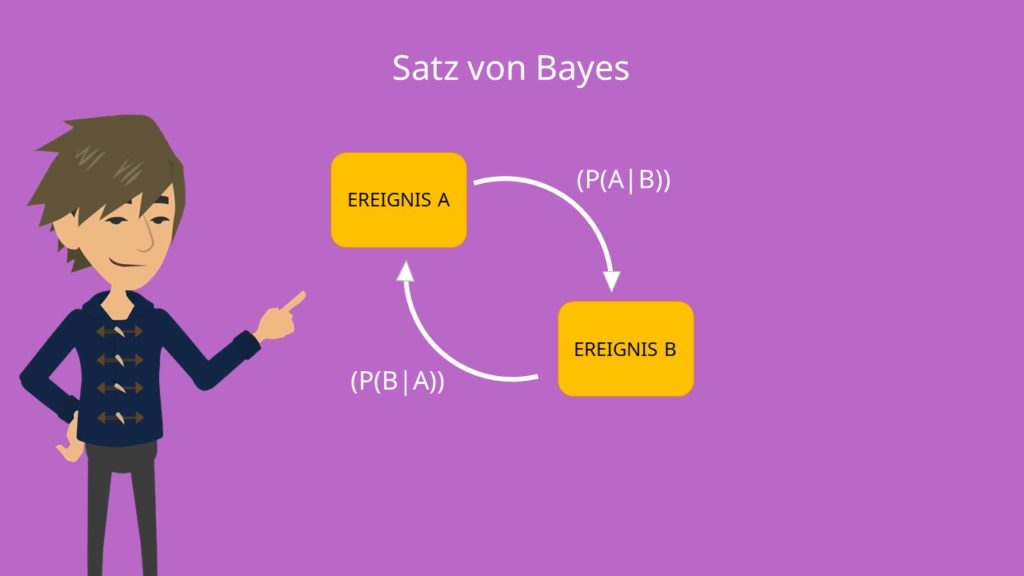
Der Satz von Bayes gehört zu den wichtigsten Sätzen der Wahrscheinlichkeitsrechnung. Er ermöglicht es die bedingte Wahrscheinlichkeit zweier Ereignisse A und B zu bestimmen, falls eine der beiden bedingten Wahrscheinlichkeiten bereits bekannt ist. Dieser mathematische Satz ist auch unter den Namen Formel von Bayes oder Bayes Theorem bekannt.
Satz von Bayes Formel
Die mathematische Formel für den Satz von Bayes sieht so aus:
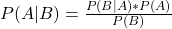
Hier ist 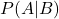 die bedingte Wahrscheinlichkeit von A falls B bereits eingetreten ist. Analog steht
die bedingte Wahrscheinlichkeit von A falls B bereits eingetreten ist. Analog steht 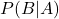 für die Wahrscheinlichkeit des Ereignisses von B unter der Bedingung, dass A eingetreten ist.
für die Wahrscheinlichkeit des Ereignisses von B unter der Bedingung, dass A eingetreten ist. 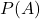 und
und 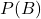 stehen jeweils für die jeweiligen Wahrscheinlichkeiten der Ereignisse.
stehen jeweils für die jeweiligen Wahrscheinlichkeiten der Ereignisse.
Satz von Bayes einfach erklärt
Wenn man also die Wahrscheinlichkeit von B unter der Bedingung von A gegeben hat kann man mit der Bayes Formel auch die bedingte Wahrscheinlichkeit
berechen, dass A eintritt, wenn B bereits eingetreten ist. Einfach gesagt ermöglicht der Satz von Bayes es Schlussfolgerungen von der anderen Seite aus zu betrachten: Man geht von dem bekannten Wert 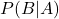 aus, ist aber eigentlich an dem Wert
aus, ist aber eigentlich an dem Wert 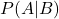 interessiert. Der Satz von Bayes folglich berechnet die umgekehrte Form der gegebenen bedingten Wahrscheinlichkeit.
interessiert. Der Satz von Bayes folglich berechnet die umgekehrte Form der gegebenen bedingten Wahrscheinlichkeit.
Satz von Bayes Beispiel
Schauen wir uns am besten gleich ein praktisches Beispiel dazu an. Stell dir vor, ein Kommilitone von dir wird nach dem Feiern von der Polizei aufgehalten und muss einen Alkoholtest machen. Bei Personen, die tatsächlich Alkohol getrunken haben, erkennt der Test das in 99,9% der Fälle.
Allerdings liefert er auch in 3% der Fälle ein positives Ergebnis, obwohl die getestete Person keinen Alkohol getrunken hat. Wir wissen also:
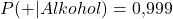
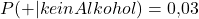
Außerdem wissen wir, dass 5% der getesteten Personen tatsächlich Alkohol konsumiert haben:
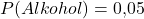
Die Wahrscheinlichkeit, dass eine getestete Person keinen Alkohol getrunken hat, liegt also bei 95%.
Der Test fällt bei deinem Kommilitonen positiv aus. Wie hoch ist die Wahrscheinlichkeit, dass er tatsächlich Alkohol konsumiert hat?
Satz von Bayes Herleitung
Diese Frage lässt sich mit Hilfe des Satzes von Bayes beantworten. Die beiden Wahrscheinlichkeiten, die wir im Zähler der Formel einsetzen müssen, haben wir gegeben. Allerdings fehlt uns noch die Wahrscheinlichkeit dafür, dass der Test positiv ausfällt. Da wir aber die beiden bedingten Wahrscheinlichkeiten gegeben haben, können wir das mit Hilfe des Satzes der totalen Wahrscheinlichkeit herleiten. Ein positives beziehungsweise negatives Testergebnis kürzen wir im Folgenden mit einem Plus beziehungsweise einem Minus ab.
Satz von Bayes Anwendung
So, jetzt müssen wir nur noch alle Werte in die Formel von vorhin einsetzen.
Da der Test positiv ausgefallen ist, hat dein Kommilitone also mit einer Wahrscheinlichkeit von 63,67% tatsächlich Alkohol getrunken.
Das wars auch schon zum Satz von Bayes! Hier findest du nochmals die allgemeine Formel: