Halbwertszeit berechnen
Wie kannst du die Halbwertszeit berechnen und was sind Zerfallsgesetz, Zerfallskonstante und Aktivität? Das erfährst du hier im Video und im Beitrag!
Inhaltsübersicht
Halbwertszeit berechnen einfach erklärt
Radioaktive Kerne zerfallen nach einer gewissen Zeit. Hast du eine Probe mit vielen Atomkernen, kannst du Aussagen dazu treffen, wie sie sich im Zerfall verhalten.
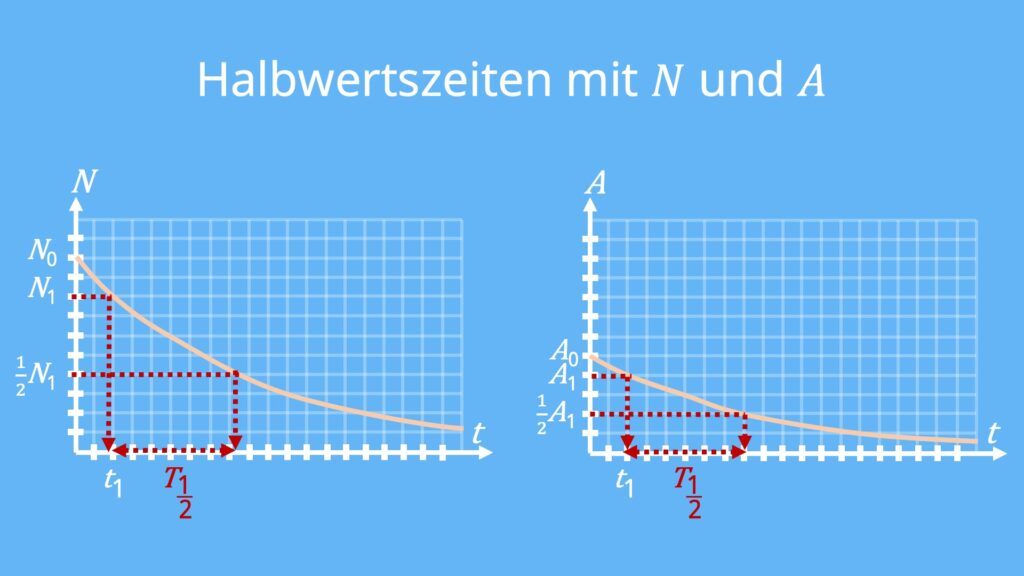
Die Halbwertszeit T1/2 ist die Zeitspanne, in der du in deiner Probe nur noch die Hälfte deiner Atomkerne übrig hast. Die andere Hälfte der Kerne ist also zerfallen. T1/2 ist somit der Zeitraum, in dem sich der Anfangsbestand deiner Atomkerne N0 halbiert hat.
Um den radioaktiven Zerfall zeitlich zu beschreiben und zu berechnen, gibt es die Zerfallsgesetze.
Zerfallsgesetz und Zerfallskonstante
Hast du eine Probe mit radioaktiv zerfallenen Atomkernen, dann nennst du N die Anzahl (Bestand) der noch nicht zerfallenen Kerne zum Zeitpunkt t. Die Menge der Atomkerne, die am Anfang in deiner Probe vorliegen, bezeichnest du mit N0. Das ist der Anfangsbestand der Kerne.
Wenn Kerne zerfallen, ändert sich also ihr Bestand mit der Zeit. Das kürzt du auch als Ṅ ab. Das ist die momentane Änderungsrate des Bestands pro Sekunde. Da die Anzahl der Kerne mit der Zeit abnimmt, ist Ṅ immer negativ.
Um wie viel Prozent sich der Bestand in einer Sekunde ändert, kannst du durch die Zerfallskonstante feststellen. Sie hat das Kürzel λ und sagt dir, wie viel Prozent der Atomkerne deiner Probe in der nächsten Sekunde durchschnittlich zerfallen wird.
![Rendered by QuickLaTeX.com \[\dot{N} = -\lambda \cdot N\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cbd66e00a46d48c9322f152c8fc98aaa_l3.png)
λ hat die Einheit 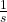 und hängt vom betrachteten „Stoff“ ab (zum Beispiel Uran).
und hängt vom betrachteten „Stoff“ ab (zum Beispiel Uran).
Du hast eine Probe mit N0 Atomkernen (= Anfangsbestand). Der Bestand N0 ändert sich mit der Zeit exponentiell.
Nun kannst du mit dem Anfangsbestand N0, mit der verstrichenen Zeit t, dem Bestand nach der Zeit Nt und der Zerfallskonstante λ den Zerfall berechnen. Du erhältst das Zerfallsgesetz:
Nt = N0 • eλ • t
Aktivität
Die Aktivität A eines radioaktiven Präparates gibt die Anzahl der radioaktiven Zerfälle pro Sekunde an. Ihre Einheit heißt Becquerel (Bq) und ist als 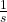 definiert.
definiert.
Somit hat die Aktivität eine ähnliche Funktion wie die momentane Änderungsrate Ṅ. Jedoch entspricht die Aktivität A der negativen Änderungsrate des Bestands N:
A = –Ṅ
Einfach gesagt bedeutet ein Bq also, dass in der nächsten Sekunde ein Zerfall stattfinden wird.
Mit der Definition der Aktivität A = –Ṅ sowie der momentanen Änderungsrate Ṅ = -λ • N und dem hergeleiteten Zerfallsgesetz N(t) = N0 • eλ • t ergibt sich folgende Beziehung für die Aktivität:
![Rendered by QuickLaTeX.com \[A(t) = \textcolor{red}{-\dot N(t)} = -(\textcolor{blue}{-\lambda \cdot N(t))} = \lambda \cdot \textcolor{orange}{N_0 \cdot e^{-\lambda t}} = A_0 \cdot e^{-\lambda t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-78a1d7d24999801a67b959afd2185be9_l3.png)
mit A0 = λ • N0.
Die Gleichung A(t) = A0 • eλ • t kannst du gemäß dem Zerfallsgesetz als Aktivitätsgesetz bezeichnen.
Halbwertszeit
Mithilfe des Zerfallsgesetzes kannst du jetzt die Halbwertszeit berechnen. Du gibst sie immer in Sekunden an, wobei ein „Stoff“ immer die gleiche Halbwertszeit hat. Du nimmst an, dass nach der Zeit T1/2 nur noch die Hälfte des Anfangsbestands N0 vorhanden ist. Zur Berechnung der Halbwertszeit hast du die beiden Formeln:
![Rendered by QuickLaTeX.com \[N(T_{1/2}) = \frac{N_0}{2} \quad \text{und} \quad N(T_{1/2}) = N_{0} \cdot e^{-\lambda \cdot T_{1/2}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6227fe73db56fd457a28592a26a7cf29_l3.png)
Du setzt gleich:
![Rendered by QuickLaTeX.com \[\frac{N_0}{2} = N_{0} \cdot e^{-\lambda \cdot T_{1/2}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cab9d020a88deb6b05f134f2fa24b36a_l3.png)
Die Gleichung kannst du nun auf beiden Seiten durch N0 teilen und logarithmieren.
![Rendered by QuickLaTeX.com \[\frac{1}{2} = e^{-\lambda \cdot T_{1/2}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f27eabb8fa5d7743aa48687121991616_l3.png)
![Rendered by QuickLaTeX.com \[ln\left( \frac{1}{2} \right) = -\lambda \cdot T_{1/2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-bc93ce8374f9cb0229303bbdf77ed2bd_l3.png)
Und kannst die Halbwertszeit T1/2 berechnen:
![Rendered by QuickLaTeX.com \[T_{1/2} = \frac{ln(2)}{\lambda}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e017a87fe2d652457ad04bf60604e76f_l3.png)
Wenn du die Gleichung nach der Zerfallskonstanten λ umformst (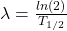 ) und in das Zerfallsgesetz (
) und in das Zerfallsgesetz (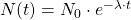 ) einsetzt, erhältst du:
) einsetzt, erhältst du:
![Rendered by QuickLaTeX.com \[N(t) = N_0 \cdot e^{-\frac{ln(2)}{T_{1/2}} \cdot t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-91f27027ee644b9646cf24bba4b03b3f_l3.png)
Das heißt, nach einer Halbwertszeit hat sich der Bestand der Atomkerne halbiert. Im Laufe der nächsten Halbwertszeit sind noch ein Viertel und nach drei Halbwertszeiten sind noch ein Achtel der ursprünglichen Atomkerne übrig.
Für die Aktivität gilt entsprechend das Aktivitätsgesetz:
![Rendered by QuickLaTeX.com \[A(t) = A_0 \cdot e^{-\frac{ln(2)}{T_{1/2}} \cdot t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c90ee3c4278021d836d1e7a95575438a_l3.png)
Zerfalls- und Aktivitätsgesetz mit Prozentsätzen
Sowohl das Zerfallsgesetz als auch das Aktivitätsgesetz gehen bei dem Bestand N und der Aktivität A von absoluten Zahlen aus. Häufig ist es aber so, dass du Prozentsätze gegeben hast.
Die Formeln können dementsprechend angepasst werden. Dabei gehst du davon aus, dass der Anfangsbestand bzw. die Anfangsaktivität jeweils 100 % beträgt.
Für das Zerfallsgesetz und das Aktivitätsgesetz ergibt sich eine einzige Gleichung, die für beide angewendet werden kann:
![Rendered by QuickLaTeX.com \[p\%(t) = 100\% \cdot e^{-\lambda t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-153539e9c7778895e93bd078c274cd6d_l3.png)
![Rendered by QuickLaTeX.com \[p\%(t) = 100\% \cdot e^{-\frac{ln(2)}{T_{1/2}} \cdot t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6c836b8aa8c4ab22bfbbe15939eecff6_l3.png)
Halbwertszeit berechnen
Die Halbwertszeit kannst du ganz einfach berechnen, indem du die jeweilige Zerfallskonstante λ in die Gleichung T1/2 = ln(2) / λ einsetzt. Wir schauen uns als Beispiel Uran-235 und Kohlenstoff-14 an.
Beispiel 1
Im Falle von Uran-235 hast du eine Zerfallskonstante von 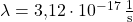 . Eingesetzt in die Gleichung ergibt sich damit für die Halbwertszeit von Uran:
. Eingesetzt in die Gleichung ergibt sich damit für die Halbwertszeit von Uran:
![Rendered by QuickLaTeX.com \[T_{1/2}^{\text{Uran-235}} = \frac{ln(2)}{3,12 \cdot 10^{-17}\,\frac{1}{\text{s}}} = 2,22163 \cdot 10^{16}\,\text{s} = 7,044 \cdot 10^8\,\text{Jahre}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7d919e38ac2a1dc343f4adbce3dbf6b8_l3.png)
Also hat Uran-235 eine Halbwertszeit von 704 Mio. Jahren!
Beispiel 2
Als weiteres Beispiel betrachtest du Kohlenstoff-14. Es hat eine Zerfallskonstante von 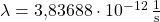 .
.
![Rendered by QuickLaTeX.com \[T_{1/2}^{\text{Kohlenstoff-14}} = \frac{ln(2)}{3,83688 \cdot 10^{-12}\,\frac{1}{\text{s}}} = 1,80654 \cdot 10^{11}\,\text{s} \approx 5729\,\text{Jahre}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f26bdd667263fc60e693633943041f80_l3.png)
Hinweis: Dein Ergebnis ist in Sekunden angegeben. Wenn du es aber in Jahre umrechnen möchtest, musst du es einfach durch das Produkt von 365 • 24 • 60 • 60 teilen, also Tage mal Stunden mal Minuten mal Sekunden. So erhältst du zum Beispiel für Kohlenstoff-14
![Rendered by QuickLaTeX.com \[\frac{1,80654 \cdot 10^{11}\, \text{s}}{(365 \cdot 24 \cdot 60 \cdot 60)} = 5729\,\text {Jahre.}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-453b781b799960567e40b09ab902b746_l3.png)
Kernspaltung
Die Kernspaltung beschreibt den Prozess, bei dem ein schwerer Atomkern in zwei kleinere Atomkerne zerlegt wird. Wenn du beispielsweise die Spaltung von Uran-235 betrachtest, kannst du hierbei eine Verringerung des Ausgangsbestands feststellen und so auch die Halbwertszeit bestimmen. Du willst mehr über den genauen Ablauf der Kernspaltung wissen? Dann schau dir unser Video dazu an!