Halbwertszeit
Was ist die Halbwertszeit und wie kannst du sie im zeitlichen Verlauf bestimmen? Das erfährst du im Video und hier im Beitrag!
Inhaltsübersicht
Halbwertszeit einfach erklärt
Radioaktive Atomkerne zerfallen über die Zeit und wandeln sich zu anderen Atomkernen um. Uran-Atomkerne wandeln sich beispielsweise durch radioaktiven Zerfall zu Thorium-Atomkernen um. Dabei kannst du für einen einzelnen Atomkern jedoch nicht bestimmen, wann genau er zerfällt.
Bei vielen Atomkernen kannst du jedoch feststellen, nach wie viel Zeit genau die Hälfte aller Atomkerne zerfallen ist. Der Zeitraum, in der nach radioaktivem Zerfall nur noch die Hälfte der Atomkerne übrig ist, nennst du die Halbwertszeit T1/2.
Nach einer Halbwertszeit T1/2 ist also die Hälfte (50%) der ursprünglichen Atomkerne noch nicht zerfallen. Nach zweimal T1/2 ist nur noch ein Viertel der Kerne (25%) übrig.
Die Halbwertszeit gibt den Zeitraum an, nachdem die Hälfte der Atomkerne eines radioaktiven Elements zerfallen ist. Die Atomkerne können dabei entweder in stabile Elemente oder weitere radioaktive Elemente zerfallen, die wiederum eine eigene Halbwertszeit haben.
Verlauf der Halbwertszeit
Die Halbwertszeit ist für jedes radioaktive Element einzigartig. Wenn du T1/2 von einem Element kennst, kannst du bestimmen, wie alt deine Probe ist. Dafür verwendest du den zeitlichen Verlauf des Verfalls.
Außerdem kannst du mit der Halbwertszeit auch die Aktivität im zeitlichen Verlauf bestimmen. Die Aktivität gibt dir an, wie viele Atomkerne in einer bestimmten Zeit, zum Beispiel in einer Sekunde, zerfallen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
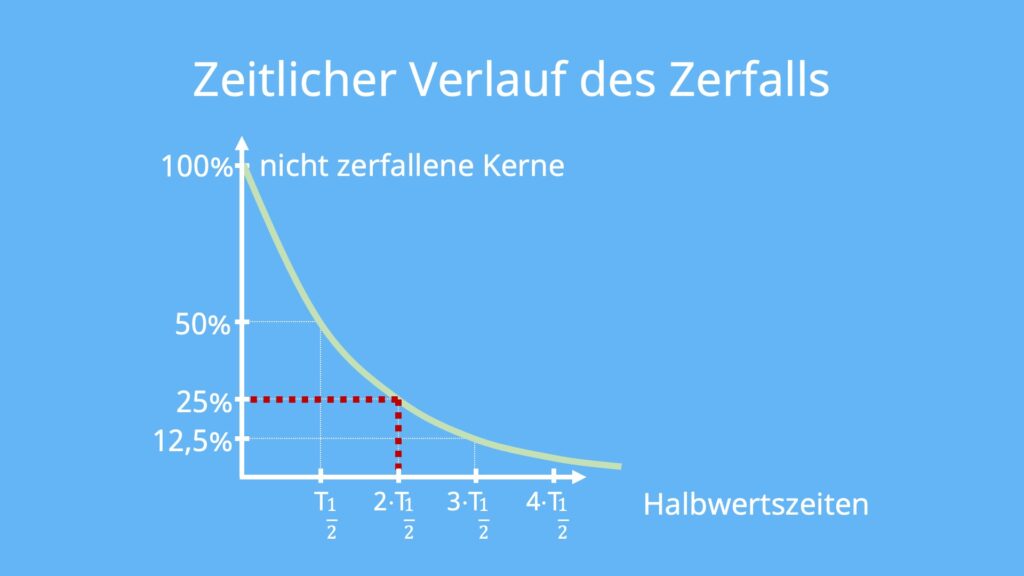
Zeitlicher Verlauf des Zerfalls
Wenn dir die Halbwertszeit einer radioaktiven Probe bekannt ist, kannst du das Alter der Probe und die Anzahl der noch nicht zerfallenen Atomkerne bestimmen. Dafür nutzt du eine grafische Darstellung des Zerfalls. Auf der y-Achse gibst du die Anteile der nicht zerfallenen Kerne in Prozent an. Auf der x-Achse gibst du die Halbwertszeiten (1 • T1/2, 2 •T1/2, 3 • T1/2 und so weiter) an.
Daraus ergibt sich eine Kurve, an der du das Alter der Probe und den Anteil der noch nicht zerfallenen Atomkerne ablesen kannst.
Beispielsweise beträgt T1/2 von Jod 131 8 Tage. Du hast vor dir eine Probe, die ursprünglich 100.000 Jod-Atomkerne besitzt. Zum Zeitpunkt deiner Untersuchung sind 16 Tage vergangen. Das heißt, du kannst mithilfe des Alters der Probe und seiner Halbwertszeit, die übrig gebliebenen Atomkerne bestimmen:
Du weißt, dass durch die Halbwertszeit T1/2 deiner Probe nach 8 Tagen nur noch 50% (50.000) der ursprünglichen Kerne (100.000) übrig sind. 16 Tage entspricht das Doppelte der Halbwertszeit, also zweimal T1/2. Schaust du also bei 2 • T1/2 auf deine Kurve, kannst du an der y-Achse den entsprechenden Prozentanteil der Atomkerne ablesen.
Bei 2 • T1/2 hast du also noch 25% deiner Atomkerne übrig. Dadurch bestimmst du, dass deine Jod-Probe von den ursprünglichen 100.000 Atomkernen nur noch 25%, also 25.000 Atomkerne hat!
Aktivität im zeitlichen Verlauf
Auch den zeitlichen Verlauf der Aktivität kannst du bestimmen. Unter der Aktivität eines radioaktiven Materials verstehst du, wie viele Zerfälle in einer bestimmten Zeit stattfinden. Dabei gilt, dass die Aktivität eines Materials direkt von der Anzahl der noch nicht zerfallenen Kerne abhängt.
Für die Aktivität im zeitlichen Verlauf kannst du wieder eine grafische Lösung anwenden. Auf der x-Achse findest du die Halbwertszeiten. Auf der y-Achse wird dir die Aktivität in Prozent angegeben. Der Graph gibt dir Auskunft darüber, wie viel Prozent der ursprünglichen Zerfälle nach einer bestimmten Halbwertszeit noch stattfinden.
Du hast beispielsweise eine Probe vor dir mit einer anfänglichen Aktivität von 1000 Zerfälle pro Sekunde. Die T1/2 deines Elements beträgt 20 Minuten. Nun kannst du mithilfe des Graphen bestimmen, wie viele Zerfälle pro Sekunde du nach einer Stunde messen wirst.
Eine Stunde entspricht genau dreimal der Halbwertszeit (3 • 20min). Du orientierst dich an der x-Achse und stellst fest, dass noch 12,5% der ursprünglichen Atomkerne vorhanden sein müssten.
Dementsprechend ist auch die Aktivität nur noch 12,5% der Anfangsaktivität. Dadurch kannst du bestimmen, dass du nach einer Stunde noch (1000 • 12,5%=) 125 Zerfälle pro Sekunde messen wirst!
Halbwertszeit Beispiele
Die Halbwertszeiten von jedem radioaktiven Element sind unterschiedlich und einzigartig. Dabei gibt es Halbwertszeiten von unter einer Sekunde bis zu Trilliarden von Jahren. In der folgenden Tabelle findest du eine Übersicht unterschiedlicher radioaktiver Elemente und deren Halbwertszeiten.
| Element | Symbol | Halbwertszeit T1/2 |
| Polonium – 214 | Po – 214 | 164 Millisekunden |
| Radon – 220 | Rn – 220 | 56 Sekunden |
| Radium – 224 | Ra – 224 | 3 Tage 16 Stunden |
| Jod – 131 | I – 131 | 8 Tage 1 Stunde |
| Kobalt – 60 | Co – 60 | 5 Jahre 4 Monate |
| Wasserstoff – 3 | H – 3 | 12 Jahre 4 Monate |
| Caesium – 137 | Cs – 137 | 30 Jahre 2 Monate |
| Radium – 226 | Ra – 226 | 1.600 Jahre |
| Kohlenstoff – 14 | C – 14 | 5.730 Jahre |
| Plutonium – 239 | Pu – 239 | 24.390 Jahre |
| Uran – 235 | U – 235 | 700.000.000 Jahre |
| Uran – 238 | U – 238 | 4.500.000.000 Jahre |
| Thorium – 232 | Th – 232 | 12.050.000.000 Jahre |
Schon gewusst? Die längste Halbwertszeit, die Wissenschaftlern bekannt ist, hat Xenon 124 (Xe – 124). Sie beträgt ganze 18 Trilliarden Jahre und ist somit eine Billion mal länger als unser Universum alt ist!
Zerfall und Aktivität im zeitlichen Verlauf — rechnerische Lösung
Den zeitlichen Verlauf von Zerfall und Aktivität kannst du nicht nur grafisch lösen, sondern auch berechnen. Wie du anhand der graphischen Lösung gesehen hast, kannst du den Zerfall und die Aktivität auf die gleiche Weise ablesen.
Deshalb kannst du sie auch auf die gleiche Weise berechnen.
Für den Zerfall rechnest du dabei mit der anfänglichen Anzahl der Atomkerne N0 (also Anzahl N zum Zeitpunkt „0“) und die Anzahl der noch nicht zerfallenen Kerne Nt zum Zeitpunkt t (Anzahl N zum Zeitpunkt „t“).
Für die Aktivität benutzt du die anfängliche Aktivität A0 (also Aktivität A zum Zeitpunkt „0“) und die Aktivität At zum Zeitpunkt t (Aktivität A zum Zeitpunkt „t“).
| Zeit | Anzahl unzerfallener Kerne Nt | Aktivität At |
| t = 0 | Nt = N0 | At = A0 |
| t = 1 • T1/2 |
 |
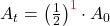 |
| t = 2 • T1/2 |
 |
 |
| t = 3 • T1/2 |
 |
 |
| … | … | … |
| t = n • T1/2 |
 |
 |
Die Variable n gibt dir also an, wie oft die Halbwertszeit vergangen ist. Sie wird bestimmt durch die vergangene Zeit t und der Halbwertszeit des jeweiligen Elements T1/2.
![Rendered by QuickLaTeX.com \[n=\frac{t}{T_{1/2}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-582cd0a1f6d68f02d32488ccbe86f806_l3.png)
Indem du n in die allgemeine Gleichung für Nt und At einsetzt, ergibt sich die Formel, mit der du den zeitlichen Verlauf des Zerfall und der Aktivität bestimmst:
![Rendered by QuickLaTeX.com \[N_{t}=\left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}}\cdot N_{0}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2e9c3523f16a77e595e70ad684276323_l3.png)
![Rendered by QuickLaTeX.com \[A_{t}=\left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}}\cdot A_{0}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-90de734ce1772c55d864b59e9ae1f8be_l3.png)
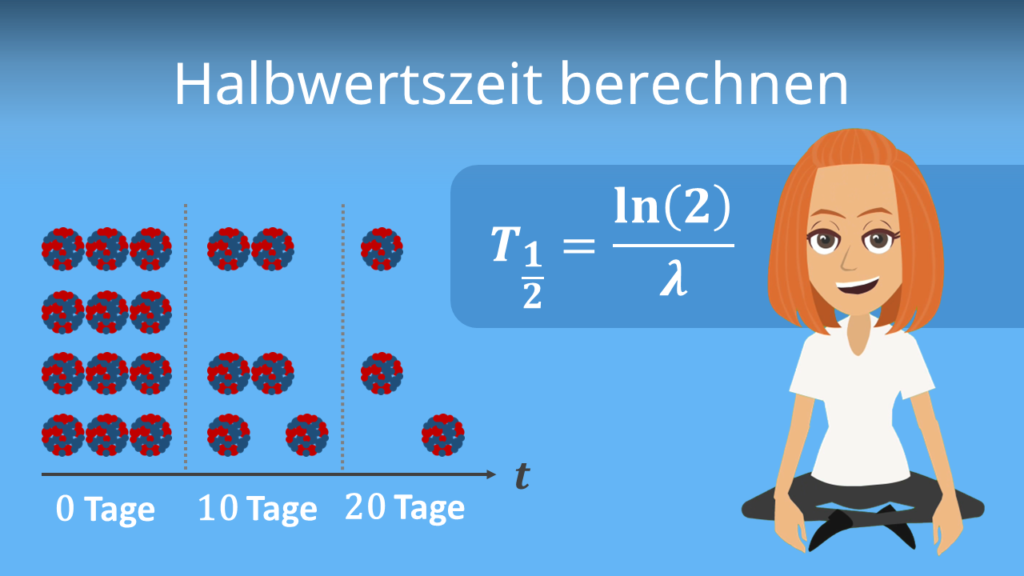
Die Halbwertszeit eines Elements wird dir jedoch nicht immer angegeben. In solchen Fällen kannst du sie auch einfach selbst berechnen. In unserem Video dazu zeigen wir dir genau, wie das funktioniert.
C-14 Methode
Die Halbwertszeit wird nicht durch äußere Einflüsse verändert. Deshalb nutzen sie Experten, um beispielsweise das Alter von Gesteinsschichten zu bestimmen. Je nachdem, wie viele radioaktive Kerne eines Elements noch nicht zerfallen sind, können sie auf das Alter rückschließen.
Wie das mit der Halbwertszeit möglich ist, zeigen wir die in unserem Video dazu!