Wärmeausdehnungskoeffizient
In diesem Beitrag zeigen wir dir, wie der Wärmeausdehnungskoeffizient definiert ist und zu welchen Berechnungen du ihn benutzen kannst. Auch geben wir dir die Ausdehnungskoeffizienten zu verschiedenen Stoffen, wie Stahl, Aluminium und Kunststoff.
Du willst das alles kurz und knapp zusammengefasst in einem Video sehen? Dann schau doch hier mal rein.
Inhaltsübersicht
Wärmeausdehnungskoeffizient einfach erklärt
In der Mechanik wird oft mit Dehnungen unter Zug- und Druckbelastungen gerechnet. Doch Werkstoffe können nicht nur durch Belastung, sondern auch durch Temperaturänderungen gedehnt werden. Der für die Ausdehnung eines Stoffes durch Veränderung der Temperatur verantwortliche Effekt wird Wärmeausdehnung genannt und durch den Wärmeausdehnungskoeffizienten beschrieben.
Der Wärmeausdehnungskoeffizient ist stoffspezifisch und temperaturabhängig. Er gibt an, wie sich ein Stoff bei bestimmter Temperatur in seinen Abmessungen verändert. Deshalb wir der Ausdehnungskoeffizient auch thermischer Ausdehnungskoeffizient genannt.
Den Wärmeausdehnungskoeffizienten kannst du weiter in einen thermischen Längenausdehnungskoeffizienten und Raumausdehnungskoeffizienten unterteilen. Beide haben eine Einheit von  oder
oder  .
.
Längenausdehnungskoeffizient
Verändert sich die Länge eines Körper durch Temperatur kannst du mit dem Längenausdehnungskoeffizienten die Wärmeausdehung rechnen. Dieser Ausdehnungskoeffizient ist definiert durch:

Er gibt an, um welche Längendifferenz 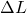 im Verhältnis zur Gesamtlänge L, sich ein fester Körper bei einer Temperaturänderung
im Verhältnis zur Gesamtlänge L, sich ein fester Körper bei einer Temperaturänderung  von genau einem Kelvin ändert.
von genau einem Kelvin ändert.
Die Formel könnte man auch wie folgt darstellen:

Hier wird die Veränderung der Länge des Körpers ins Verhältnis zur Temperatur gesetzt. Die Veränderung wird über die Ableitung der beiden Größen beschrieben.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Thermischer Ausdehnungskoeffizient
Der temperaturabhängige Ausdehnungskoeffizient  ist dabei eine Werkstoffkonstante, die die spezifische Ausdehnung für das Material angibt. Es gilt:
ist dabei eine Werkstoffkonstante, die die spezifische Ausdehnung für das Material angibt. Es gilt:

Die Längenänderung ist also ein Produkt aus dem thermischen Ausdehnungskoeffizienten  , der Ursprungslänge
, der Ursprungslänge  und der Temperaturänderung
und der Temperaturänderung  .
.

Der thermische Ausdehnungskoeffizient wird in der Einheit 1/K angegeben.
Wärmeausdehnungskoeffizienten Tabelle
Hier siehst du einige thermische Ausdehnungskoeffizienten für unterschiedliche Materialien wie zum Beispiel die Wärmeausdehnungskoeffizienten von Stahl, Aluminium und Kunststoff.
| Längenausdehnungskoeffizient Alpha bei Feststoffen | |
| Material | Alpha in 10^-6/K bei 20 Grad |
| Acryl | 90 |
| Aluminium | 23.1 |
| Beton | 12 |
| Blei | 28.9 |
| Borosilikatglas | 3.3 |
| Chrom | 4.9 |
| Diamant | 1.18 |
| Eisen | 11.8 |
| Germanium | 5.8 |
| Glas | 8.5 |
| Gold | 14.2 |
| Graphit | 1,9-2,9 |
| Invar | 0,55-1,2 |
| Kupfer | 16.5 |
| Magnesium | 24.8 |
| Mangan | 21.7 |
| Kochsalz | 40 |
| Nickel | 13.4 |
| Platin | 8.8 |
| Polypropylene | 150 |
| PVC | 52 |
| Quarzglas | 0.54 |
| Silber | 18.9 |
| Silizium | 2.6 |
| Stahl | 11-13,0 |
| Technische Keramik | 2-13,0 |
| Titan | 8.6 |
| Wolfram | 4.5 |
| Zerodur | 0-0,1 |
| Zink | 30.2 |
| Zinkcyanid | -18.1 |
| Zinn | 22 |
| Zirconiumwolframat | -8.7 |
Können sich die thermischen Verformungen nicht ungehindert ausbreiten, zum Beispiel wegen eines Auflagers, werden thermische Spannungen hervorgerufen.
Auch können wir die Gesamtdehnung in eine elastische und eine thermische Dehnung aufteilen.

Hier gilt zudem das Hookesche Gesetz . Setzen wir beide Dehnungen in die Gleichung ein, erhalten wir:

Wärmeausdehnungskoeffizient Beispiel
Schauen wir uns doch mal ein konkretes Beispiel an. Ein 10 m langer Kupferstab erwärmt sich von 20°C auf 35°C. Um wieviel mm verlängert sich der Balken durch die Erwärmung?

Der Temperaturunterschied beträgt 15°C.

Wir setzen unsere Werte ein. Damit ergibt sich eine Verlängerung des Balkens von 0,24 mm:

Raumausdehnungskoeffizient
Der räumliche Wärmeausdehnungskoeffizient gibt die Volumenzunahme  bezüglich der Temperaturänderung
bezüglich der Temperaturänderung  eines Körpers an. In einer Formel ausgedrückt ist das eine partielle Ableitung, wobei die Gößen Druck p und dieTeilchenzahl N konstant gehalten werden.
eines Körpers an. In einer Formel ausgedrückt ist das eine partielle Ableitung, wobei die Gößen Druck p und dieTeilchenzahl N konstant gehalten werden.
