Biegung
In diesem Artikel zeigen wir dir die Theorie zur Biegung auf und berechnen anschließend eine Durchbiegung eines Balkens.
Falls du das alles lieber kurz und knapp in einem Video erklärt bekommen möchtest, dann schau doch hier mal rein.
Inhaltsübersicht
Biegung einfach erklärt
Bei einer Biegung betrachtest du in der technischen Mechanik vor allem schlanke Bauteile. Diese werden durch eine von außen einwirkende Kraft gekrümmt. Es werden dabei zwei Arten von Biegungen unterschieden. Die gerade und die schiefe Biegung.
- gerade Biegung: die Kraft, die die Biegung verursacht, wirkt in Richtung einer der Hauptträgheitsachsen des Querschnitts des betrachteten Körpers
- schiefe Biegung: Kraft wirkt in eine andere Richtung als die Hauptträgheitsachsen eines Querschnitts
Ebenfalls erzeugt eine angreifende Kraft, die eine Krümmung an einem Bauteil verursacht, im oberen Teil des Bauteils eine Zugspannung und im unteren einen Druck. Die Belastung durch die Kräfte ist dabei in den Randgebieten des Bauteiles deutlich höher als weiter in diesem. An der Stelle, an der sich Druck- und Zugkraft gegenseitig kompensieren, befindet sich die sogenannte neutrale Faser. Durch die Kompensation der beiden Kräfte ist diese spannungsfrei.
Biegemoment
Das Biegemoment ist wie der Name schon sagt das Moment, das einen Körper verbiegt. Das Moment für eine Biegung Mb kann dabei nach folgender Formel berechnet werden:

Dabei ist F die wirkende Querkraft und x der Abstand der Kraft vom Festlager. Die Einheit der Formel ist [Nm].
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Biegespannung
Die Biegespannung baut auf dem Biegemoment auf und ergibt sich aus:

Hier ist Mb das Moment der Biegung und W ist das Widerstandsmoment . Du siehst, dass die Spannung von dem Moment abhängt. Das liegt daran, dass ein Biegemoment erst an deinem Balken angreifen muss, bevor sich überhaupt eine Spannung aufbauen kann und es zu einer Krümmung kommen kann.
Widerstandsmoment
Das Widerstandsmoment W entspricht dem axialen Flächenmoment zweiten Grades I
geteilt durch den größten Abstand der Randfaser zur neutralen Faser 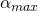 .
.

Wenn du mehr zu diesem erfahren möchtest, kannst du dir unser Video dazu anzusehen.
Durchbiegung berechnen
Werden lange, dünne Bauteile quer zur Bauteilachse mit einem Biegemoment belastet, entstehen Zug- und Druckspannungen. Bei einem Balken führt dies zu einer Durchbiegung. Diese möchten wir jetzt berechnen.
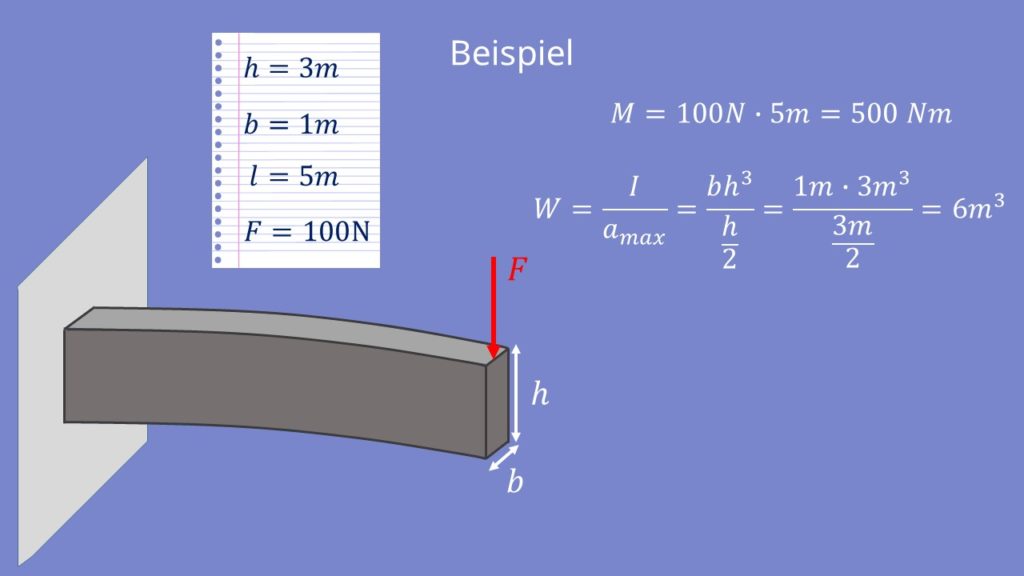
Wir haben eine Kraft F, die von oben auf das Balkenende drückt. Der Balken wird im Bereich der Zugbelastung gedehnt und im Bereich der Druckbelastung gestaucht. In der Mitte des Balkens können wir die neutrale Faser sehen. Diese wird weder gedehnt noch gestaucht und ist somit spannungslos. Die Spannungen sind am Rand am höchsten und werden nach innen geringer. Wir nehmen an, dass sich Zug- und Druckspannungen gleichmäßig über das gesamte Bauteil verteilen.
Biegespannung und Biegemoment berechnen
Nehmen wir an, unser Balken ist 3 Meter hoch, 1 Meter breit und 5 Meter lang. Es wirkt eine Kraft von 100 Newton.
Das Moment ist nun folgendes:

Nun benötigen wir noch das Widerstandsmoment.

Der Abstand der Randfaser von der neutralen Faser beträgt h halbe, also 1,5 Meter. Für das Flächenträgheitsmoment setzen wir die Formel  ein. Wir erhalten also ein Widerstandsmoment von 6 Kubikmetern. Nun setzen wir dieses Ergebnis in die Formel für die Biegespannung ein.
ein. Wir erhalten also ein Widerstandsmoment von 6 Kubikmetern. Nun setzen wir dieses Ergebnis in die Formel für die Biegespannung ein.

Wir erhalten 83 Pascal Biegespannung.
Je nach Geometrie des Balkens ändert sich das Widerstandsmoment und das Biegemoment. Zum Beispiel bei einem Balken, der von zwei Festlagern gehalten wird:
Hier lautet die Formel für das Biegemoment:

Die Kraft verteilt sich dabei auf beide Balkenenden.