Wahrscheinlichkeitsrechnung
Du fragst dich, was Wahrscheinlichkeitsrechnung ist und willst verschiedene Beispiele dazu sehen? Hier und im Video erfährst du alles rund um dieses spannende Thema!
Inhaltsübersicht
Wahrscheinlichkeitsrechnung einfach erklärt
Schau dir Wahrscheinlichkeitsrechnung gleich an einem Beispiel an:
Wenn du zum Beispiel eine Münze wirfst, erhältst du zufällig Kopf oder Zahl. Du weißt vorher nicht, was herauskommt. Aber du kannst berechnen, wie groß die Wahrscheinlichkeit für ein Ergebnis ist (z.B. für Kopf). Damit beschäftigt sich die Wahrscheinlichkeitsrechnung.
In unserem Beispiel sind Kopf und Zahl beide gleich wahrscheinlich. Du hast also eine Fifty-Fifty-Chance: Die Wahrscheinlichkeit für Kopf ist ½ (oder 50 %) und die für Zahl auch.
In der Wahrscheinlichkeitsrechnung ermittelst du Wahrscheinlichkeiten für bestimmte Ereignisse in einem Zufallsexperiment, zum Beispiel die Wahrscheinlichkeit für Kopf beim Werfen einer Münze. In der Mathematik zählst du die Wahrscheinlichkeitsrechnung zum Teilgebiet der Stochastik.
Baumdiagramm der Wahrscheinlichkeitsrechnung
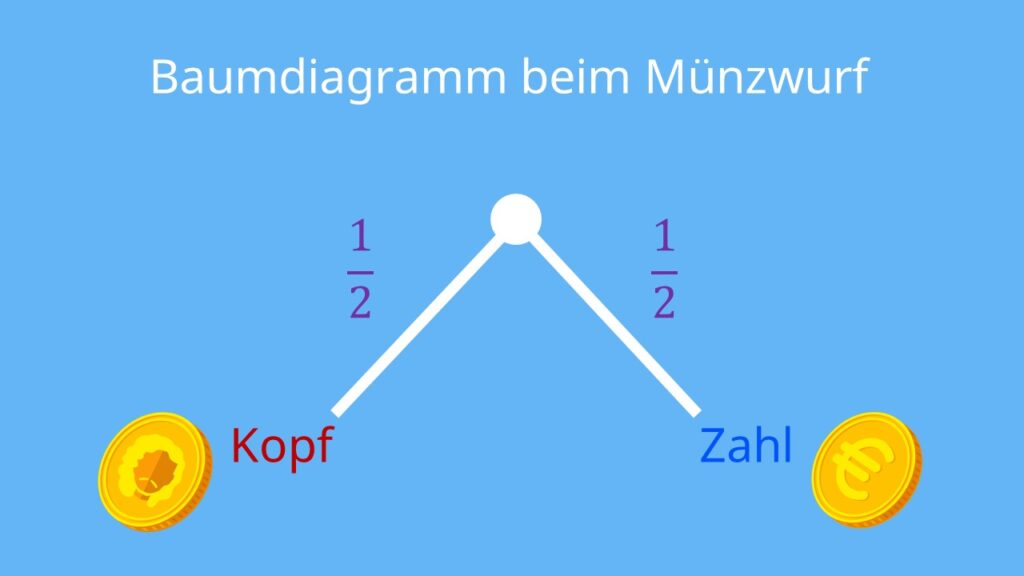
Das Zufallsexperiment mit der Münze kannst du an einem Baumdiagramm
darstellen. Dabei zeichnest du ganz oben einen Knoten und dann zwei Linien nach unten, weil es zwei mögliche Ergebnisse gibt (Kopf und Zahl). Du nennst diese Linien Pfade. Neben sie schreibst du die Wahrscheinlichkeiten für das jeweilige Ergebnis, hier also ½.
An einem Baumdiagramm, auch Ereignisbaum genannt, kannst du ganz leicht verstehen, wie dein Zufallsexperiment aufgebaut ist. Das hilft dir bei der Wahrscheinlichkeitsrechnung enorm!
Laplace Regel
Wenn du wie im vorherigen Beispiel eine Münze wirfst, dann sind Kopf und Zahl gleich wahrscheinlich. Beide Ergebnisse haben eine Chance von ½. Wenn alle möglichen Ergebnisse die gleiche Wahrscheinlichkeit haben, sprichst du von einem Laplace-Experiment .
-
Weiteres Beispiel: Du wirfst einen Würfel. Jede Zahl zwischen 1 und 6 ist dann gleich wahrscheinlich. Es handelt sich also um ein Laplace-Experiment. Die Chance für jede Zahl liegt bei
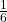 .
. -
Nicht alle Experimente sind Laplace-Experimente. Stell dir vor, in einer Lostrommel sind 2 Gewinne und 8 Nieten und du ziehst ein Los. Dann ist es wahrscheinlicher, dass du eine Niete ziehst. Die beiden Ergebnisse haben also nicht die gleiche Wahrscheinlichkeit.
Bei Laplace-Experimenten kannst du die Wahrscheinlichkeit mit einer Formel berechnen. Dabei teilst du die Anzahl der betrachteten Ergebnisse durch die Anzahl aller möglichen Ergebnisse (beim Würfel 6 mögliche Ergebnisse, nämlich 1 bis 6). Die Wahrscheinlichkeit, eine 3 oder eine 5 (also 2 betrachtete Ergebnisse) zu würfeln ist also:
![Rendered by QuickLaTeX.com \[\frac{\text{\textcolor{orange}{betrachtete Ergebnisse}}}{\text{\textcolor{teal}{alle möglichen Ergebnisse}}}=\frac{\textcolor{orange}{2}}{\textcolor{teal}{6}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-bb6fdeae7d60009bdf1fd3e8dc7dd882_l3.png)
Zufallsexperimente
Die Münze, der Würfel und die Lose — all das sind Zufallsexperimente. Das bedeutet, dass es mindestens zwei mögliche Ausgänge gibt und du vorher nicht weißt, was herauskommen wird.
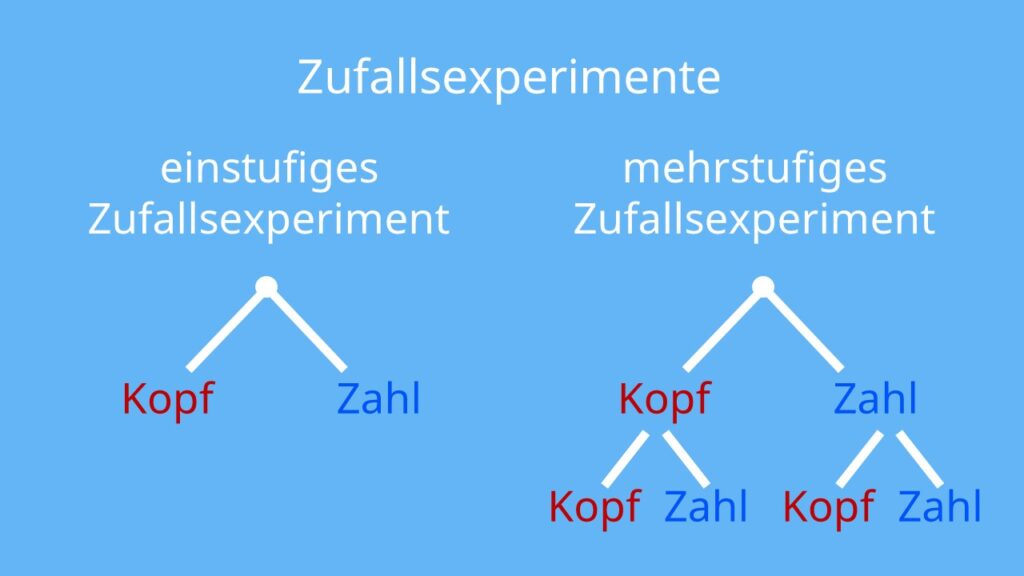
Du unterscheidest zwei verschiedene Arten von Zufallsexperimenten: einstufige und mehrstufige.
- Bisher hast du nur einstufige Zufallsexperimente betrachtet. Das heißt, dass du deinen Versuch nur einmal durchgeführt hast. Zum Beispiel wurde die Münze einmal geworfen.
- führst du Experimente aber öfter durch. Dann sprichst du von einem mehrstufigen Zufallsexperiment.
Du kannst auch mehrstufige Zufallsexperimente in ein Baumdiagramm einzeichnen. Es hat dann so viele Ebenen, wie du Versuchsdurchgänge machst:
Übrigens: Wenn du bei mehrstufigen Zufallsexperimenten Wahrscheinlichkeiten berechnen sollst, helfen dir oft die Pfadregeln weiter. Wir erklären sie dir in einem extra Video !
Die Begriffe Ergebnis und Ereignis bedeuten nicht das Gleiche. Schau dir das am Wurf eines Würfels an:
- Ein Ergebnis ist alles, was du würfeln kannst, also 1, 2, 3, 4, 5 und 6. Alle möglichen Ergebnisse zusammen nennst du Ergebnismenge .
- Ein Ereignis kannst du selbst definieren. Zum Beispiel sind E1 = „die Zahl ist größer als 4“ und E2 = „die Zahl ist gerade“ Ereignisse. Je nach Ergebnis beim Würfeln kannst du dann entscheiden, ob das Ereignis eingetreten ist oder nicht. Wenn du zum Beispiel eine 5 würfelst, dann ist E1 eingetreten, aber E2 nicht.
Abhängige und unabhängige Ereignisse
Du kennst jetzt schon mehrstufige Zufallsexperimente, bei denen alle Ebenen im Baumdiagramm genau gleich aussehen. Das ist aber nicht immer der Fall. Schau dir zum Beispiel folgendes Zufallsexperiment an:
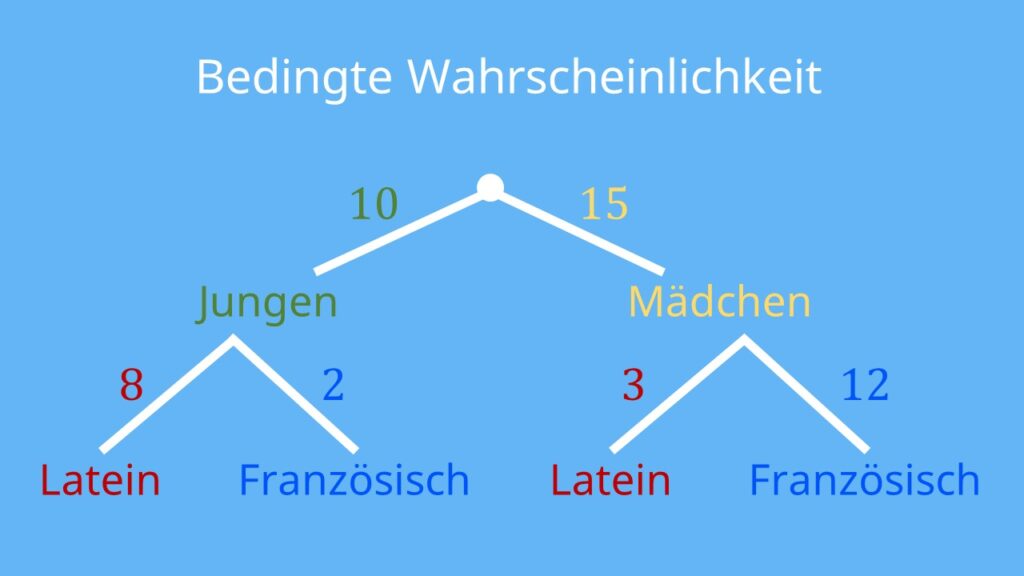
Aus einer Klasse wird zufällig ein Schüler ausgewählt. In der Klasse sind 10 Jungen und 15 Mädchen.
- Von den Jungen lernen 8 Latein und 2 Französisch.
- Von den Mädchen lernen 3 Latein und 12 Französisch.
Wenn du einen Jungen auswählst, ist es viel wahrscheinlicher, dass er Latein lernt, als wenn du ein Mädchen auswählst. Denn bei den Jungen lernen 8 von 10 Latein (also 80 %) und bei den Mädchen nur 3 von 15 (das sind nur 20 %).
Wie wahrscheinlich es ist, dass ein Schüler Latein lernt, hängt also davon ab, ob du einen Jungen oder ein Mädchen auswählst. Die beiden Ereignisse sind also abhängig. Besteht kein Zusammenhang, nennst du sie unabhängig . Das ist zum Beispiel bei zweimal Würfeln der Fall.
Wenn du bei abhängigen Ereignissen Wahrscheinlichkeiten berechnen willst, hilft dir der Satz von Bayes weiter. Du möchtest noch mehr Formeln zur Wahrscheinlichkeitsrechnung kennenlernen? Dann schau hier vorbei!
Übrigens: Bei abhängigen Ereignissen ist die Darstellung in einer Vierfeldertafel oft leichter als im Baumdiagramm. Schau dir also gleich unser Video dazu an!
Expertenwissen: Binomialkoeffizient
Stell dir vor, du möchtest deine Wand in zwei Farben streichen. Zur Auswahl stehen gelb, orange, rot und grau. Du wählst zufällig zwei Farben aus. Es gibt dann viele verschiedene Kombinationsmöglichkeiten, zum Beispiel gelb–orange, orange–rot, rot–grau, …. Aber wie viele sind es genau?
Das verrät dir der Binomialkoeffizient . Er besteht aus zwei Zahlen, die übereinander in einer Klammer stehen. Oben steht die Anzahl der Möglichkeiten insgesamt (Abkürzung: n). Unten steht die Anzahl der Farben, die du auswählst (Abkürzung: k):
![Rendered by QuickLaTeX.com \[\text{Kombinationsmöglichkeiten} = \binom{\textcolor{teal}{n}}{\textcolor{blue}{k}} = \binom{\textcolor{teal}{4}}{\textcolor{blue}{2}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7447608642f136f81d35c96540ecf614_l3.png)
Du kannst den Binomialkoeffizienten ganz leicht mit einer Formel berechnen. Das Ausrufezeichen steht dabei für die Fakultät :
![Rendered by QuickLaTeX.com \[\binom{\textcolor{teal}{n}}{\textcolor{blue}{k}}=\frac{\textcolor{teal}{n}!}{\textcolor{blue}{k}!\cdot (\textcolor{teal}{n}-\textcolor{blue}{k})!} = \frac{\textcolor{teal}{4}!}{\textcolor{blue}{2}!\cdot (\textcolor{teal}{4}-\textcolor{blue}{2})!} = \frac{\textcolor{teal}{4\cdot 3\cdot 2\cdot 1}}{\textcolor{blue}{(2\cdot 1)}\cdot (2 \cdot 1)} = \frac{24}{4} = 6\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dc692a89656f74d801fe0190954c30c7_l3.png)
Tipp: Wahrscheinlich hast du auf deinem Taschenrechner eine Taste für den Binomialkoeffizienten, nämlich nCr. Dann musst du ihn nicht per Hand ausrechnen!
Der Binomialkoeffizient spielt eine große Rolle bei der Binomialverteilung und der Bernoulli-Formel . Damit kannst du dann nicht nur die Anzahl der Möglichkeiten ausrechnen, sondern auch Wahrscheinlichkeiten. Besonders bei langen Zufallsexperimenten mit sehr vielen Durchgängen hilft sie dir weiter.
Wahrscheinlichkeitsrechnung Beispiele
Jetzt kennst du schon viele wichtige Begriffe der Wahrscheinlichkeitsrechnung. Schau dir zum Schluss noch zwei typische Beispiele an: Das Urnenmodell und die Lottoziehungen.
Wahrscheinlichkeitsrechnung am Urnenmodell
Beim Urnenmodell stellst du dir eine Urne vor, also ein Gefäß, in das du nicht hineinschauen kannst. Darin sind Kugeln, meist in unterschiedlichen Farben, zum Beispiel 3 blaue und 2 rote. Du ziehst nun aus der Urne. Die Chance, eine blaue Kugel zu ziehen, liegt dann bei  und die für rot bei
und die für rot bei  . Wenn du mehrfach ziehst, kannst du außerdem unterscheiden, ob du die Kugel nach jeder Ziehung zurücklegst
oder nicht
.
. Wenn du mehrfach ziehst, kannst du außerdem unterscheiden, ob du die Kugel nach jeder Ziehung zurücklegst
oder nicht
.
Oft findest du in der Wahrscheinlichkeitsrechnung Aufgaben, die mit dem Urnenmodell zu tun haben — entweder ganz offensichtlich oder indirekt, wie zum Beispiel beim Lotto.
Wahrscheinlichkeitsrechnung beim Lotto
Beim Lotto wählst du aus 49 Zahlen 6 aus. Wie groß ist die Wahrscheinlichkeit, dass du alle 6 richtig hast? Das kannst du mit dem Binomialkoeffizienten berechnen. Dabei ist die Anzahl der Möglichkeiten insgesamt 49 (n = 49) und du wählst 6 aus (k = 6). Insgesamt gibt es also
![Rendered by QuickLaTeX.com \[\binom{\textcolor{teal}{49}}{\textcolor{blue}{6}} = 13.983.816\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-05027cfc655009a918f48cd8315c179c_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{13 938 816 }=0,000.000.072\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a4541e19742f498b68fcdb3000dd8470_l3.png)
Kombinatorik
Die Wahrscheinlichkeitsrechnung hängt eng mit der Kombinatorik zusammen. Dabei beschäftigst du dich damit, wie viele Kombinationsmöglichkeiten es zum Beispiel beim Ziehen von Kugeln gibt. Wenn du mehr darüber erfahren willst, schau dir gleich unser Video an!