Dichte Wasser
Die Dichte des Wassers sorgt, dafür, dass die Eiswürfel in deinem Getränk nicht untergehen. Wie genau das funktioniert, erklären wir dir hier und in unserem Video dazu!
Inhaltsübersicht
Was ist die Dichte des Wassers?
Die Dichte ist eine wichtige physikalische Eigenschaft. Sie sagt aus, wie viel Masse ein bestimmtes Volumen eines Stoffes hat. Außerdem spielt sie eine wichtige Rolle bei der Herstellung und Identifikation von Materialien.
Vor allem bei Wasser ist die Dichte besonders. Sie beträgt ungefähr 1 kg pro ein Liter (= 1 dm3) Wasser. Die Dichte des Wassers wird dabei mit sinkender Temperatur immer höher und erreicht ihren Höhepunkt bei 4°C. Danach sinkt die Dichte wieder, bis das Eis gefriert. Dieses Phänomen bezeichnest du als die Dichteanomalie von Wasser.
Die exakte Dichte von Wasser bei 4°C und einem normalen Druck beträgt 997 kg/m³.
Die Dichte (ρ) sagt aus, wieviel Masse einer Substanz sich in einem gewissen Volumen befindet. Dabei sind Substanzen mit höherer Dichte in der Regel schwerer als welche mit niedrigerer Dichte. Es gibt verschiedene Einheiten zur Messung der Dichte, aber die gebräuchlichste Einheit ist Kilogramm pro Kubikmeter (kg/m³).
Dichte Wasser Einheit
Die Einheit der Dichte des Wassers ist Kilogramm pro Kubikmeter (kg/m³) oder Gramm pro Kubikzentimeter (g/cm³). Beide Einheiten drücken das Verhältnis von Masse zu Volumen aus.
Dabei wird kg/m³ am häufigsten verwendet, um die Dichte von Flüssigkeiten und Gasen zu messen. Die Einheit g/cm³ nutzt du häufiger für die Dichte von Feststoffen.
Gut zu wissen: Du kannst die Einheiten ganz einfach umrechnen. Ein Kubikmeter (m³) ist das Tausendfache eines Kubikdezimeters (dm3), also eines Liters. Somit lassen sich 997 kg/m³ in 0,997 kg/dm³ oder 0,000997 kg/cm³ umrechnen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Dichte Wasser Temperatur Tabelle
Die Dichte von Wasser ist temperaturabhängig. Die folgende Tabelle zeigt, wie sich die Dichte von reinem Wasser je nach Temperatur verändert.
Die Dichte wird hierbei in kg/m³ bei einem Druck von 1 bar ≙ 1013 mbar angegeben:
| Grad Celcius | Dichte in kg/m3 |
| 0 | 999,843 |
| 4 | 999,975 |
| 10 | 999,702 |
| 20 | 998,207 |
| 30 | 995,65 |
| 40 | 992,22 |
| 50 | 988,04 |
| 60 | 983,20 |
| 70 | 977,76 |
| 80 | 971,79 |
| 90 | 965,31 |
| 99,9 | 958,42 |
Übrigens: Da Wasser auch häufig mit Luft in Kontakt ist, wird die Luft im Wasser gelöst. Diese hat jedoch nur einen sehr geringen Einfluss auf die Wasserdichte. Auch der Druck hat nur wenig Einfluss auf die Dichte des Wassers.
Die Anomalie des Wassers
Die Dichteanomalie des Wassers bezieht sich auf das ungewöhnliche Verhalten der Dichte von Wasser bei verschiedenen Temperaturen. Die meisten Stoffe haben nämlich im festen Zustand eine höhere Dichte als im flüssigen.
Im Gegensatz dazu erreicht Wasser bei einer Temperatur von 4°C seine höchste Dichte. Bei weiterer Abkühlung wird es jedoch wieder weniger dicht, bis es schließlich in Form von Eis vorliegt.
Der Grund dafür ist, dass die Wassermoleküle zunächst immer enger auf einen Fleck zusammenrücken. Das hat mit der Molekularbewegung zu tun. Dabei bewegen sich Teilchen bei hoher Temperatur stärker als bei niedriger.
Unter 4°C fangen die Moleküle an, sich an die Form von Eiskristallen anzupassen. Bei dieser Form lagern sich die Wassermoleküle jedoch sechseckig an, wodurch Zwischenräume entstehen. Dadurch sinkt wieder die Dichte.
Dieses Verhalten führt übrigens dazu, dass Eis auf Wasser schwimmt.
Dichte Wasserdampf
Um die Dichte von Wasserdampf zu berechnen, kannst du das ideale Gasgesetz verwenden. Ihre Formel sieht so aus:
![Rendered by QuickLaTeX.com \[V= \frac{n \cdot R \cdot T }{p} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a0915dc5e97ad1ddfed64a6a67efc11f_l3.png)
Die Variablen stehen dabei für folgende Werte:
-
 = Volumen in m
= Volumen in m
-
 = Stoffmenge des Gases in Mol
= Stoffmenge des Gases in Mol -
 = absolute Temperatur in Kelvin
= absolute Temperatur in Kelvin -
 = Druck in Pascal
= Druck in Pascal -
 = universelle
Gaskonstante
. Sie hat immer den Wert
= universelle
Gaskonstante
. Sie hat immer den Wert  .
.
Kelvin ist die absolute Temperatur. Du kannst die Temperatur in °C umrechnen, indem du 273,15 addierst:
![Rendered by QuickLaTeX.com \[T(\text{in K}) = T_{\mathrm{C}}(\text{in }^{\circ}\mathrm{C})+ 273,15\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b982f848a813363878f98de5888fcaf5_l3.png)
Die Formel für die Stoffmenge n ist:
![Rendered by QuickLaTeX.com \[n = \frac{m}{M}.\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2736fc2926b4ee60397e838fec4e1a8d_l3.png)
Hierbei beschreibt 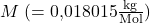 das Molekulargewicht von Wasser. Setzt du diese Formeln in die Gasgleichung ein und formst um, so erhältst du für die Dichte folgende Formel:
das Molekulargewicht von Wasser. Setzt du diese Formeln in die Gasgleichung ein und formst um, so erhältst du für die Dichte folgende Formel:
![Rendered by QuickLaTeX.com \[V= \frac{m \cdot R \cdot (T_{\mathrm{C}} + 273,15)}{M\cdot p}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fc2d816e527fadc9112285c703f7f29f_l3.png)
![Rendered by QuickLaTeX.com \[\Leftrightarrow \rho &=\frac{m}{V}= \frac{p\cdot M}{R \cdot(T_{\mathrm{C}} + 273,15)}.\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0eca5d3329384f722d727fb521730439_l3.png)
Mit dieser Formel kann die Dichte von Wasser relativ genau bestimmt werden, da sich reale Gase annähernd wie ideale Gase verhalten. In der folgenden Tabelle ist die Dichte von Wasserdampf für verschiedene Temperaturen und Drücke aufgelistet. Die Dichte wurde dabei unter Verwendung des idealen Gasgesetzes berechnet:
| Druck in Bar | Temperatur in Grad Celcius | Dichte in kg/m3 |
| 1 | 100 | 0,588 |
| 1 | 200 | 0,464 |
| 1 | 300 | 0,383 |
| 1 | 400 | 0,326 |
| 1 | 500 | 0,284 |
| 10 | 200 | 4,64 |
| 10 | 300 | 3,83 |
| 10 | 400 | 3,26 |
| 10 | 500 | 2,84 |
| 100 | 400 | 32,6 |
| 100 | 500 | 28,4 |
| 100 | 600 | 25,1 |
Dichte des Wassers — häufigste Fragen
-
Was ist das Gewicht von Wasser?
Die Dichte von Wasser beträgt 1,0 g/cm³, was bedeutet, dass ein Liter Wasser eine Masse von 1 kg hat und ein Volumen von 1000 cm³ einnimmt.
-
Was ist die Dichte Wasser in g/cm3?
Bei einer Temperatur von 4°C und einem Druck von einer Atmosphäre beträgt die Dichte von Wasser 1000 kg/m3 oder 1 g/cm3. Da die Dichte von Wasser 1 g/cm3 beträgt, haben Masse und Volumen dieselbe Größe. Kurz gesagt entspricht 1 Liter Wasser einem Kilogramm Masse.
-
Was ist die Dichte von Eis?
0,918 g/cm³ ist die Dichte von hexagonalem, gewöhnlichem Eis bei 0°C. Sie ist geringer ist als die Dichte von flüssigem Wasser. Dieses Phänomen wird als Dichteanomalie des Wassers bezeichnet. Aufgrund dessen schwimmt Eis auf der Wasseroberfläche, was zur Bildung von Eisschollen und Eisbergen führt.
Schweres Wasser
Jetzt weißt du bestens über die Dichte des Wassers Bescheid! Es gibt aber eine Wasserart, deren Dichte noch höher ist als die Dichte von herkömmlichem Wasser. Ein solches Wasser bezeichnest du als schweres Wasser. Schau dir jetzt unser Video zu dem Thema an, um alles darüber zu erfahren. Bis gleich!

