Dichte berechnen
Die Dichte eines Gegenstandes ist eine seiner wichtigsten physikalischen Eigenschaften. In diesem Beitrag erfährst du, was die Dichte ist, wie du sie berechnen kannst und bekommst einen Überblick der wichtigsten Materialien.
In unserem Video Dichte berechnen zeigen wir dir Schritt für Schritt die Berechnung und die Einheiten anhand von Beispielen.
Im zweiten Video Dichte (Massendichte) erklären wir dir die wichtigsten Zusammenhänge der Dichte. Außerdem schauen wir an, wie du die Einheiten der Dichte ganz leicht ineinander umrechnen kannst.
Inhaltsübersicht
Was ist Dichte?
Die Dichte mit dem Formelzeichen  („Rho“) gibt an, welche Masse
(„Rho“) gibt an, welche Masse  ein Objekt mit einem bestimmen Volumen
ein Objekt mit einem bestimmen Volumen  besitzt.
besitzt.
Du kannst dir die Dichte wie einen kleinen Automaten vorstellen: Als Input gibst du ihr das Volumen eines Gegenstandes; als Output bekommst du seine Masse. Die Dichte eines Objektes gibt dir also seine Masse pro Volumen an.

Die Dichte selbst ist als ein Quotient definiert.
Die Dichte  eines Gegenstandes (
eines Gegenstandes ( ist das kleine Rho aus dem griechischen Alphabet) ist der Quotient aus seiner Masse
ist das kleine Rho aus dem griechischen Alphabet) ist der Quotient aus seiner Masse  und seinem Volumen
und seinem Volumen  . Du sagst auch „Dichte ist gleich Masse pro Volumen“
. Du sagst auch „Dichte ist gleich Masse pro Volumen“

Die Einheit für  ist
ist
Kilogramm pro Kubikmeter, ![Rendered by QuickLaTeX.com [\rho] = \frac{\displaystyle{\text{kg}}}{\displaystyle{\text{m}^3}}.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0d32991a2304a8d9134a81fbe0bcf3a6_l3.png)
Die Dichte ist also das Verhältnis zwischen wie schwer ein Objekt ist (Masse  ) und wie viel Platz von diesem eingenommen wird (Volumen
) und wie viel Platz von diesem eingenommen wird (Volumen  ). Sie ist zudem eine Materialeigenschaft. Die Dichte ist daher zwar unabhängig von Größe und Form eines Objekts, sie ändert sich aber mit der Temperatur und dem Druck.
). Sie ist zudem eine Materialeigenschaft. Die Dichte ist daher zwar unabhängig von Größe und Form eines Objekts, sie ändert sich aber mit der Temperatur und dem Druck.
Dichte Formel
Die Formel ist ein Quotient aus zwei Größen: Der Masse  und dem Volumen
und dem Volumen  . Du hörst dafür oft Dichte Rho ist gleich Masse pro Volumen
. Du hörst dafür oft Dichte Rho ist gleich Masse pro Volumen

Wenn du die Masse und das Volumen gegeben hast, dann kannst du die Dichte berechnen, indem du die Masse durch das Volumen teilst.
Masse  aus
aus  und
und  bestimmen
bestimmen
Was aber, wenn du die Dichte  und das Volumen
und das Volumen  gegeben hast? Dann kannst du durch Umformen der Formel die Masse ausrechnen. Du bekommst als Resultat, dass die Masse
gegeben hast? Dann kannst du durch Umformen der Formel die Masse ausrechnen. Du bekommst als Resultat, dass die Masse  das Produkt aus Dichte
das Produkt aus Dichte  und Volumen
und Volumen  ist
ist

Volumen  aus
aus  und
und  bestimmen
bestimmen
Umgekehrt kannst du auch das Volumen bestimmen, wenn du  und
und  hast. Dafür rechnest du Masse
hast. Dafür rechnest du Masse  durch Dichte
durch Dichte 

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Dichte Einheit
Einheiten von physikalischen Größen sind von zentraler Bedeutung. Bei der Dichte teilst du eine Masse  durch ein Volumen
durch ein Volumen  . Die Einheit von
. Die Einheit von  ist also die Einheit der Masse geteilt durch die Einheit des Volumens. Oft findest du dafür Kilogramm (
ist also die Einheit der Masse geteilt durch die Einheit des Volumens. Oft findest du dafür Kilogramm ( ) pro Kubikmeter (
) pro Kubikmeter (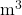 )
)
![Rendered by QuickLaTeX.com [\rho] = \frac{\displaystyle{\text{kg}}}{\displaystyle{\text{m}^3}}.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0d32991a2304a8d9134a81fbe0bcf3a6_l3.png)
Die Masse kannst du aber auch in Gramm ( ) und das Volumen in Kubikzentimeter (
) und das Volumen in Kubikzentimeter ( ) angeben. Möchtest du
) angeben. Möchtest du  von Kilogramm pro Kubikmeter auf Gramm pro Kubikzentimeter umrechnen, dann musst du nur dein Ergebnis durch 1000 teilen. Umgekehrt musst du mit 1000 mutliplizieren. In Symbolen sieht das so aus
von Kilogramm pro Kubikmeter auf Gramm pro Kubikzentimeter umrechnen, dann musst du nur dein Ergebnis durch 1000 teilen. Umgekehrt musst du mit 1000 mutliplizieren. In Symbolen sieht das so aus
Kilogramm pro Kubikmeter in Gramm pro Kubikzentimeter: 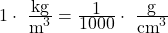
oder Gramm pro Kubikzentimeter in Kilogramm pro Kubikmeter: 
Manchmal wird das Volumen auch in Liter ( ) angegeben. Die Umrechnung von Kilogramm pro Kubikmeter auf Kilogramm pro Liter ist aber identisch zur vorherigen Umrechnung. Du hast also einen Faktor von 1000 zwischen den beiden Einheiten
) angegeben. Die Umrechnung von Kilogramm pro Kubikmeter auf Kilogramm pro Liter ist aber identisch zur vorherigen Umrechnung. Du hast also einen Faktor von 1000 zwischen den beiden Einheiten
Kilogramm pro Kubikmeter in Kilogramm pro Liter: 
oder Kilogramm pro Liter in Kilogramm pro Kubikmeter: 
Dichte berechnen Beispiel 1: Direkte Anwendung der Formel
Wir haben einen kleinen Nagel mit einem Volumen von  und einer Masse von
und einer Masse von 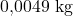 gegeben. Um mit dieser Information die Dichte berechnen zu können, verwenden wir direkt die Formel
gegeben. Um mit dieser Information die Dichte berechnen zu können, verwenden wir direkt die Formel

Angenommen, du möchtest wissen, aus welchem Material der Nagel besteht. Du kannst dafür einen kurzen Blick auf die Tabelle am Ende des Artikels werfen. Dort ist die Dichte von Stahl mit  angegeben. Unser Nagel ist also ein Stahlnagel.
angegeben. Unser Nagel ist also ein Stahlnagel.
Dichte berechnen Beispiel 2: Würfel aus Gold
Sagen wir, du hast einen Würfel aus Gold mit einer Kantenlänge von  . Du möchtest wissen, wie schwer so ein Würfel sein wird. Dazu berechnen wir in einem ersten Schritt das Volumen dieses Würfels
. Du möchtest wissen, wie schwer so ein Würfel sein wird. Dazu berechnen wir in einem ersten Schritt das Volumen dieses Würfels

Im nächsten Schritt schauen wir kurz in die Tabelle rein und finden heraus, dass Gold eine Dichte von  besitzt. Wir müssen jetzt nur noch die Formel auf die Masse
besitzt. Wir müssen jetzt nur noch die Formel auf die Masse  umstellen
umstellen

Dichte berechnen Beispiel 3: Einheit umrechnen und Masse bestimmen
In diesem Beispiel haben wir einen Kupferdraht mit einem Radius von  und einer Länge von
und einer Länge von  gegeben. Die Dichte des Kupfers beträgt
gegeben. Die Dichte des Kupfers beträgt  . Wir möchten von diesem Kupferdraht die Masse in Kilogramm berechnen.
. Wir möchten von diesem Kupferdraht die Masse in Kilogramm berechnen.
Hierfür bestimmen wir im ersten Schritt das Volumen des Kupferdrahtes. Dazu stellen wir es uns als ein Zylinder vor. Das Volumen ist dann

Im nächsten Schritt müssen wir die Einheit von  umrechnen, da sie in Gramm pro Kubikzentimeter angegeben ist. Wir müssen dafür nur mit 1000 multiplizieren
umrechnen, da sie in Gramm pro Kubikzentimeter angegeben ist. Wir müssen dafür nur mit 1000 multiplizieren

Jetzt können wir die Masse berechnen

Dichte (Massendichte)
Die Dichte, genauer die Massendichte, ist eine physikalische Eigenschaft eines Körpers, die vom Material des Körpers abhängt und als Quotient von Masse und Volumen definiert ist

Wenn die „Konzentration“ der Masse innerhalb eines Körpers überall gleich ist, so findest du dafür die Bezeichnung homogener Körper. In diesem Fall kannst du die Gesamtmasse als Produkt aus Dichte und Volumen berechnen

Alle wichtigen Infos findest du einfach und Schritt für Schritt erklärt in unserem Video zur Dichte (Massendichte) . Schau es dir unbedingt an!
Definition Dichte
Die Masse und das Volumen sind quantitative Aussagen über einen Gegenstand. Sie ändern sich, wenn du den Gegenstand vergrößerst oder verkleinerst. Solche Größen heißen extensive Größen.
Das Verhältnis aus Masse und Volumen heißt Dichte (oder etwas präziser Massendichte)  und ist hingegen eine intensive Größe. Sie bleibt unverändert, egal wie sehr du die Größe eines Gegenstandes veränderst. Die Dichte eines Gegenstandes ist also allein vom Material abhängig, aus dem der Gegenstand besteht.
und ist hingegen eine intensive Größe. Sie bleibt unverändert, egal wie sehr du die Größe eines Gegenstandes veränderst. Die Dichte eines Gegenstandes ist also allein vom Material abhängig, aus dem der Gegenstand besteht.
Wenn du dir zum Beispiel einen kleinen Goldwürfel vorstellst und ihn gedanklich vergrößerst oder verkleinerst, dann bleibt der Wert von  unverändert. Die Masse und das Volumen verändern sich aber dabei.
unverändert. Die Masse und das Volumen verändern sich aber dabei.
Als Verhältnis der Masse  und dem Volumen
und dem Volumen  kannst du die Dichte
kannst du die Dichte  mit
mit

ausrechnen. Die Einheit der Dichte  , notiert als
, notiert als ![Rendered by QuickLaTeX.com [ \rho ]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e7c62841736c5f034b4356ee28adaaec_l3.png) , ist
, ist
![Rendered by QuickLaTeX.com [\rho] = \frac{\displaystyle{\text{kg}}}{\displaystyle{\text{m}^3}} = 10^{-3} \ \frac{\displaystyle{\text{g}}}{\displaystyle{\text{cm}^3}} = 10^{-3} \ \frac{\displaystyle{\text{kg}}}{\displaystyle{\text{L}}}.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-383b90c196b584e510fd774b9063fe68_l3.png)
Die letzte Einheit, Kilogramm pro Liter, wird insbesondere bei Flüssigkeiten verwendet. Im nächsten Abschnitt schauen wir uns die Umrechnung zwischen diesen Einheiten an.
Hinweis: Auch wenn die Dichte eines Gegenstandes von seiner Form und Größe unabhängig ist, so ist sie von der Temperatur abhängig. Das liegt daran, dass die Dichte sowohl von der Masse der Atome, aus denen ein Gegenstand besteht, als auch deren Abstand voneinander abhängt. Durch Temperatureinflüsse kannst du den Abstand verändern. Für gewöhnlich steigt die Dichte mit abnehmender Temperatur. Es gibt aber Elemente , die eine sogenannte Dichteanomalie vorweisen. Ein Beispiel dafür ist Wasser.
Dichte umrechnen
Im vorherigen Abschnitt hatten wir dir unterschiedliche Einheiten für  gezeigt. In diesem Abschnitt schauen wir uns ein paar konkrete Beispiele an, wie wir zwischen diesen Einheiten umrechnen können.
gezeigt. In diesem Abschnitt schauen wir uns ein paar konkrete Beispiele an, wie wir zwischen diesen Einheiten umrechnen können.
Kilogramm pro Kubikmeter ( ) in Gramm pro Kubikzentimeter (
) in Gramm pro Kubikzentimeter ( )
)
Als Beispiel hierfür nehmen wir Gold. Der Wert von  ist hier
ist hier

Um jetzt von Kilogramm pro Kubikmeter auf Gramm pro Kubikzentimeter umzurechnen, müssen wir sowohl Kilogramm in Gramm und Kubikmeter in Kubikzentimeter umwandeln

Allgemein gilt also die folgende Umrechnung

Das heißt, wenn du von Kilogramm pro Kubikmeter auf Gramm pro Kubikzentimeter rechnen möchtest, dann teilst du durch 1000. Umgekehrt, also von Gramm pro Kubikzentimeter auf Kilogramm pro Kubikmeter, multiplizierst du mit 1000.
Kilogramm pro Kubikmeter ( ) in Kilogramm pro Liter (
) in Kilogramm pro Liter ( )
)
Für diese Umrechnung nehmen wir als Beispiel Wasser. Hier hat  einen Wert von
einen Wert von

Zur Umrechnung in Kilogramm pro Liter musst du wissen, dass ein Kubikdezimeter gleich ein Liter entspricht

Damit erhalten wir

Das heißt, dass ein Liter Wasser in etwa ein Kilogramm wiegt.
Allgemein verläuft die Umrechnung von Kilogramm pro Kubikmeter auf Kilogramm pro Liter identisch zur vorherigen Umrechnungen. Wir haben also

Dichte messen
Um die Dichte zu bestimmen, brauchst du zwei Größen: Die Masse und das Volumen. Wenn du ein Objekt hast und herausfinden möchtest, aus welchem Material es besteht, dann brauchst du nur seine Masse und sein Volumen bestimmen. Wenn du dann  ausrechnest, kannst du mit Hilfe von Tabellen das Material bestimmen.
ausrechnest, kannst du mit Hilfe von Tabellen das Material bestimmen.
Dichte messen bei festen Gegenständen
Wenn du einen Gegenstand gegeben hast, dann brauchst du zwei Sachen, um die Dichte berechnen zu können: Die Masse und das Volumen des Gegenstandes.
Masse und Volumen bei festen Gegenständen
Bei festen Gegenständen kannst du die Masse häufig mit einer Waage bestimmen. Beim Volumen hängt es stark davon ab, welche Form der Körper besitzt. Hat der Körper eine einfache geometrische Form , etwa ein Würfel oder ein Zylinder, dann kannst durch Bestimmen der Maße (Länge, Breite, Höhe, Radius, etc.) mit den entsprechenden Formeln das Volumen berechnen.
Bei kompliziert geformten Körper kannst du das Volumen mit Hilfe der Überlaufmethode bestimmen. Du hast hier im Wesentlich zwei Messzylinder, von denen einer bis zum Rand mit Wasser gefüllt ist. Aufgrund des Archimedische Prinzips wird beim vollständigen Eintauchen des Körpers entsprechend des Volumens eine bestimmte Menge Wasser verdrängt. Die Menge kannst du dann im zweiten Messzylinder auffangen und so das Volumen bestimmen.
Dichte im Diagramm
Damit die Messung etwas genauer wird, untersuchst du den Gegenstand bei unterschiedlichen Werte für die Masse und das Volumen. Zu jedem Paar (Masse, Volumen) kannst du die Dichte berechnen. Wenn du dann deine Ergebnisse in einem Graphen einträgst, solltest du eine Gerade durch den Ursprung erhalten.
Die Steigung  dieser Gerade entspricht der Dichte des untersuchten Gegenstandes. Wir können also die Dichte auch als einen Proportionalitätsfaktor zwischen Masse und Volumen verstehen. Je höher die Steigung
dieser Gerade entspricht der Dichte des untersuchten Gegenstandes. Wir können also die Dichte auch als einen Proportionalitätsfaktor zwischen Masse und Volumen verstehen. Je höher die Steigung  , desto größer ist
, desto größer ist  .
.
Dichte messen bei Flüssigkeiten
Bei Flüssigkeiten brauchst du die gleiche Information, um die Dichte berechnen zu können. In diesem Fall wird aber oft statt Kubikmeter die Einheit Liter ( ) oder Milliliter (
) oder Milliliter ( ) für das Volumen verwendet.
) für das Volumen verwendet.
Zwei gängige Messgeräte sind das Aräometer und die Mohrsche Waage. Beide basieren auf dem Archimedische Prinzip und der damit erklärten Auftriebskraft .
Dichte ausgewählter Materialien
In diesem Abschnitt geben wir dir eine Übersicht verschiedener Materialien und deren Dichte. Die Werte werden für eine Temperatur von 20°C angegeben.
| Material | Massendichte |
| Wasser |  |
| Luft |  |
| Stahl |  |
| Beton |  |
| Gold |  |
| Aluminium |  |
| Ethanol |  |
| Blei |  |
| Eisen |  |
| Holz |  |
| Kupfer |  |
| Granit |  |
Luft hat also eine sehr geringe Dichte von etwa einem Kilogramm pro Kubikmeter; Stahl hingegen eine ziemlich hohe von etwa 8000 Kilogramm pro Kubikmeter. Bei Holz hängt der Dichtewert von der betrachteten Holzart ab. Die Werte liegen aber zwischen 200 bis 1200 Kilogramm pro Kubikmeter.
Die Werte hängen aber stark vom Druck und der Temperatur ab. In Metallen beispielsweise sind die Atome eng beieinander und entsprechend ist die Dichte hoch. Flüssigkeiten haben einen mittleren Dichtebereich. Eine Ausnahme hier ist Quecksilber, das eine Dichte von  besitzt. Gase haben für gewöhnlich sehr geringe Dichten.
besitzt. Gase haben für gewöhnlich sehr geringe Dichten.
Dichte berechnen — häufigste Fragen
(ausklappen)
Dichte berechnen — häufigste Fragen
(ausklappen)-
Wie rechne ich Liter und Milliliter sauber in Kubikmeter um, ohne mich bei Zehnerpotenzen zu vertun?Du rechnest über die Grundregel 1 L = 1 dm³ = 0,001 m³ und 1 mL = 1 cm³ = 10⁻⁶ m³. Das liegt daran, dass bei Volumen jede Längen-Umrechnung dreifach eingeht. Beispiel: 250 mL = 250 · 10⁻⁶ m³ = 2,5 · 10⁻⁴ m³.
-
Wie bestimme ich die Dichte von einem porösen Stoff wie Holz oder Schaumstoff, wenn Luft in den Hohlräumen steckt?Du musst zuerst festlegen, ob du die Rohdichte (mit Poren) oder die Materialdichte (ohne Poren) meinst. Für die Rohdichte misst du Masse und Außenvolumen, auch wenn Luft in den Poren ist. Die Materialdichte bekommst du nur, wenn du das Porenvolumen separat bestimmst.
-
Warum ändert sich die Dichte von Gasen so stark mit Druck und Temperatur, aber die von Festkörpern oft nur wenig?Bei Gasen ändert sich das Volumen stark, deshalb ändert sich die Dichte stark mit Druck und Temperatur. Das lässt sich oft näherungsweise mit dem idealen Gasgesetz erklären:
 . In Festkörpern sind Teilchen eng gepackt, daher sind sie kaum kompressibel und dehnen sich nur wenig aus.
. In Festkörpern sind Teilchen eng gepackt, daher sind sie kaum kompressibel und dehnen sich nur wenig aus.
-
Welche Fehler passieren oft bei der Wasserverdrängung, wenn der Gegenstand schwimmt oder Wasser an ihm hängen bleibt?Häufige Fehler sind unvollständiges Eintauchen bei schwimmenden Gegenständen und zusätzliche Wassermengen durch anhaftende Tropfen. Ein schwimmender Körper verdrängt nur so viel Wasser, bis Auftrieb und Gewicht passen, das ist nicht sein Gesamtvolumen. Abhilfe: Beschweren oder festhalten und Tropfen abstreifen.
Dichte Wasser
Der Dichtewert von Wasser lässt sich leicht merken: 1 Liter Wasser wiegt etwa ein Kilogramm. Das heißt Wasser besitzt einen  -Wert von etwa einem Kilogramm pro Liter.
-Wert von etwa einem Kilogramm pro Liter.
Wasser gehört zu den Elementen, die eine sogenannte Dichteanomalie vorweisen. Das bedeutet, die Dichte von Wasser ist bei 4°C am größten. Das wiederum steht im starken Kontrast zum „normalen“ Dichteverhalten, bei dem die Dichte mit abnehmender Temperatur steigt. Du interessierst dich mehr für die Dichteanomalie des Wassers? Dann solltest du auf jeden Fall einen Blick auf unseren Beitrag dazu werfen.
Wasser ist für unser Leben von zentraler Bedeutung. Wenn du dein Wissen über Wasser erweitern möchtest, dann empfehlen wir dir unseren ausführlichen Beitrag zur Dichte von Wasser. Hier erfährst du auch wichtige Fakten über Wasserdampf.





