Kernspaltung
Was ist die Kernspaltung und warum entsteht dabei Energie? Das erfährst du in unserem Video und in unserem Beitrag.
Inhaltsübersicht
Kernspaltung einfach erklärt
Die Kernspaltung oder Atomspaltung beschreibt den Prozess, bei dem ein schwerer Atomkern in zwei kleinere Atomkerne zerlegt wird. Dabei werden mehrere Neutronen und Energie freigesetzt. Die Energie nennst du Kernenergie. Damit es zu einer Kernspaltung kommen kann, muss der schwere Atomkern mit einem langsamen Neutron beschossen werden.
Die bekannteste Kernspaltung ist die von Uran-235. Sie wird in Kernkraftwerken zur Energieerzeugung genutzt. Dabei zerfällt der schwere Uran-Kern in zwei mittelschwere Atomkerne. Oft sind das Barium und Krypton. Bei jeder einzelnen, solcher Spaltreaktionen wird Energie abgegeben.
Der Grund für die Energiefreisetzung ist dabei die Tatsache, dass die Gesamtmasse der Kerne nach der Spaltung kleiner ist als die Masse vor der Spaltung (= Massendefekt). Das heißt, die fehlende Masse wurde in Energie umgewandelt. Der Zusammenhang zwischen der Verringerung der Masse und der freigesetzten Energie lässt sich mit der berühmten Formel E = m • c2 erklären.
Kernspaltung Uran
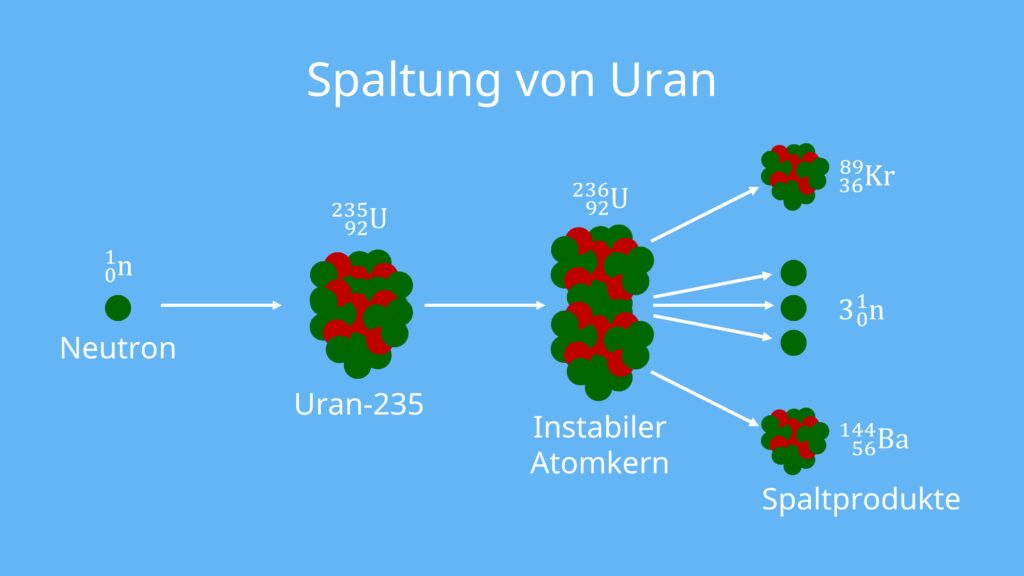
Um eine Kernspaltung von Uran herbeizuführen, wird sein Atomkern mit langsamen Neutronen beschossen. Das Uran-235 nimmt ein Neutron auf, wodurch es zu Uran-236 wird. Jetzt ist es aber instabil und wird innerhalb kurzer Zeit in mehrere Teile zerfallen. Der Atomkern spaltet sich in zwei mittelschwere Atomkerne (häufig Krypton-89 und Barium-144) und es entstehen zwei bis drei zusätzliche Neutronen.
Die Spaltung von Uran wird also gezielt herbeigeführt. Deswegen sprichst du auch von einer induzierten Kernspaltung. Wenn ein Atomkern ohne äußere Beeinflussung gespalten wird, handelt es sich um eine spontane Kernspaltung.
Du bezeichnest die Atomkerne nach der Spaltung auch als Spaltfragmente oder Spaltprodukte.
Für die Kernspaltung von Uran-235 gibt es verschiedene Spaltungsmöglichkeiten. Häufig erfolgt die Spaltung in einen leichteren Atomkern (Massenzahl etwa 90) und in einen schwereren Atomkern (Massenzahl etwa 140).
Ein Beispiel für eine Spaltmöglichkeit von Uran-235 ist die Spaltung in Barium-144 (Ba) und Krypton-89 (Kr):
![Rendered by QuickLaTeX.com \[^{1}_{0} \mathsf{n} \ + \ ^{235}_{92}\mathsf{U} \ \rightarrow \ ^{236}_{92} \mathsf{U} \ \rightarrow \ ^{144}_{56} \mathsf{Ba} \ + \ ^{89}_{36} \mathsf{Kr} \ + \ 3 \cdot \ ^{1}_{0} \mathsf{n}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c0a7cebdf943712053f2256f76b783f7_l3.png)
Weitere Spaltmöglichkeiten sind die Spaltungen von Uran-235 in Caesium-143 (Cs) und Rubidium-90 (Rb) oder in Xenon-143 (Xe) und Strontium-90 (Sr).
Ursache der frei werdenden Energie
Bei der Kernspaltung von Uran wird Energie freigesetzt. Die Ursache dafür kannst du aus dem Massenverhältnis vor und nach der Spaltung erklären.
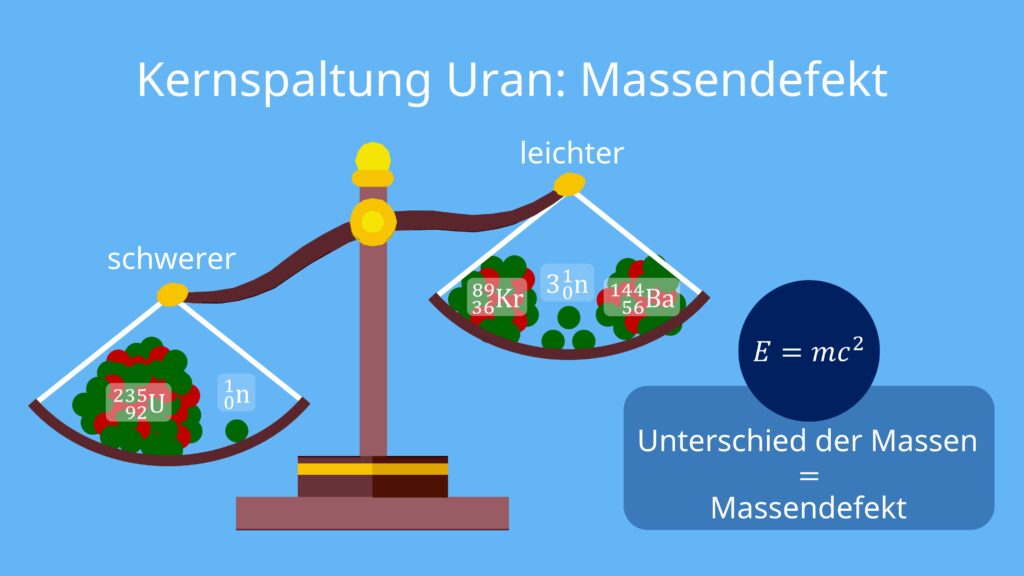
Stell dir vor, du wiegst den schweren Atomkern Uran-235 und das Neutron vor der Spaltung sowie die mittelschweren Atomkerne Barium-144, Krypton-89 und die frei werdenden Neutronen nach der Spaltung. Dann stellst du fest, dass das Gesamtgewicht vor der Kernspaltung größer ist als das Gesamtgewicht nach der Spaltung. Den Unterschied in den Massen bezeichnest du als Massendefekt .
Die Masse nach der Spaltung ist also kleiner als die Masse vor der Spaltung. Um zu verstehen, wieso dabei dann plötzlich Energie freigesetzt wird, kannst du die berühmteste Formel der Physik über die Äquivalenz von Masse und Energie von Albert Einstein verwenden.
![Rendered by QuickLaTeX.com \[\textcolor{blue}{E} = \textcolor{red}{m} \cdot \textcolor{olive}{c}^2\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0b79a8adde0f6d8523ce0d24a068d02f_l3.png)
Hier ist m die Masse eines Objekts und c die Lichtgeschwindigkeit. Der Buchstabe E steht für die Ruheenergie, also diejenige Energie, die das Objekt besitzt, wenn es sich als Ganzes nicht bewegt.
Masse und Energie sind also bis auf eine Konstante das Gleiche. Für unsere Kernspaltung bedeutet das Folgendes: Die Masse nach der Spaltung ist kleiner, damit aber auch die Energie. Nun ist Energie eine Erhaltungsgröße
. Und genau die „fehlende“ Energie entspricht der freigesetzten Energie. Wenn wir den Massendefekt mit 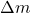 bezeichnen, dann ergibt sich für die freigesetzte Energie
bezeichnen, dann ergibt sich für die freigesetzte Energie 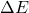 :
:
![Rendered by QuickLaTeX.com \[\Delta E = \Delta m \cdot c^2\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e6346e46b742ce5aec8b8808d25fc1f8_l3.png)
Energiefreisetzung berechnen
Mit dem Unterschied der Kernmassen und der Einsteinschen Formel kannst du jetzt die freigesetzte Energiemenge bei der Kernspaltung von Uran-235 berechnen. Hierzu benötigen wir zunächst die Atommassen des Uran-235, des Neutrons, des Barium-144 und des Krypton-89. Die Kernmassen in der atomaren Masseeinheit u findest du in unserer Tabelle:
| Stoff | Atommasse (atomare Masseneinheit u) |
| Uran | 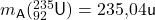 |
| Neutron | 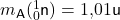 |
| Barium | 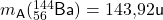 |
| Krypton | 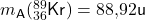 |
Vor der Spaltung beträgt die Atommasse etwa 236,05u.
![Rendered by QuickLaTeX.com \[M_{\mathsf{vor}} = m_{\mathsf{A}} (^{235}_{92} \mathsf{U}) \ + \ 1 \cdot m_{\mathsf{A}} (^{1}_{0} \mathsf{n}) = 235,04 \mathsf{u} \ + \ 1,01 \mathsf{u} = 236,05 \mathsf{u}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7d209f6964016c4fe3a6084cbcccd780_l3.png)
Nach der Spaltung beträgt die Atommasse etwa 235,87u.
![Rendered by QuickLaTeX.com \[M_{\mathsf{nach}} = m_{\mathsf{A}} (^{144}_{56} \mathsf{Ba}) \ + \ m_{\mathsf{A}} (^{89}_{36} \mathsf{Kr}) \ + \ 3 \cdot m_{\mathsf{A}} (^{1}_{0} \mathsf{n}) = 143,92 \mathsf{u} \ + \ 88,92 \mathsf{u} \ + \ 3 \cdot 1,01 \mathsf{u} = 235,87 \mathsf{u}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c26345aeb7fcf5bc228bee0445d32c3e_l3.png)
So ergibt sich der Massendefekt aus der Differenz von beiden berechneten Atommassen und beträgt 0,18u.
![Rendered by QuickLaTeX.com \[\Delta m = M_{\mathsf{vor}} - M_{\mathsf{nach}} = 236,05 \mathsf{u} \ - \ 235,87 \mathsf{u} = 0,18 \mathsf{u}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4b53684f0f8211fe4b7b6ecbb18de6bf_l3.png)
Der Massendefekt kann in die Formel für die Äquivalenz von Masse und Energie eingesetzt werden. Dabei entspricht 1u • c2 einem Wert von 931,494 Megaelektronenvolt (MeV). Die freigesetzte Energiemenge für eine einzige Kernspaltung beträgt somit etwa 168 MeV.
![Rendered by QuickLaTeX.com \[\Delta E = \Delta m \cdot c^2 = 0,18 \cdot \mathsf{u} \cdot c^2 = 0,18 \cdot 931,49 \mathsf{MeV} = 167,67 \mathsf{MeV}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8e3d3ba0c8ff02ee12c52e01f999a2ca_l3.png)
Hinweis: Bei der Berechnung mit den genauen Atommassen ergibt sich ein Wert von ziemlich genau 173 MeV. Damit hat Uran eine extrem hohe Energiedichte. Denn nur ein Kilogramm Uran kann eine Energiemenge von ungefähr 24 Millionen kWh erzeugen. Das entspricht der Energiemenge von rund 3.000 Tonnen Steinkohle.
Kettenreaktionen
Die bei den Spaltungen entstehenden Neutronen können weitere Kernspaltungen anregen, wenn sie abgebremst werden. Dadurch entstehen wieder Neutronen, die nach einer Abbremsung ebenfalls Kernspaltungen herbeiführen können und so weiter. Es kommt zu einem Vorgang, der sich von selbst fortsetzt, nämlich zu einer Kettenreaktion.
- Wenn die Kettenreaktion nicht beeinflusst wird, sprichst du von einer ungesteuerten Kettenreaktion. Das ist zum Beispiel bei einer Atombombe der Fall.
- Es ist allerdings auch möglich, die Anzahl der Neutronen zu beschränken und damit auf die Kettenreaktion Einfluss zu nehmen. Eine beeinflusste Kettenreaktion nennst du dann auch gesteuerte Kettenreaktion. So etwas passiert zum Beispiel im Kernreaktor eines Kernkraftwerks.
Kernspaltung Entdeckung
Die Entdeckung des Neutrons im Jahre 1932 durch James Chadwick führte zu unmittelbaren Folgerungen für die experimentelle Kernphysik. Da das Neutron elektrisch neutral ist, kann es nämlich die Atomkerne durchdringen.
Die ersten Experimente, die das ausnutzten, waren der Beschuss von Uran mit Neutronen durch Enrico Fermi und seinen Forschungskollegen in Rom im Jahre 1934. Er entdeckte dabei die verschiedenen Spaltprodukte, aber seine Ergebnisse wurden damals mit Skepsis betrachtet.
Otto Hahn, Lise Meitner und Fritz Strassmann wiederholten anschließend die Experimente, bis Otto Hahn schließlich das Spaltfragment Barium beim Beschuss von Uran mit Neutronen entdeckte.
Daraufhin bewiesen sie, dass das Barium die Folge eines Prozesses war, der heute als Kernspaltung bekannt ist. Die Ergebnisse wurden von Hahn und Strassmann im Jahre 1939 veröffentlicht. Meitner und ihr Neffe Otto Frisch brachten im selben Jahr eine theoretische Erklärung der Beobachtungen heraus.
Aus diesem Grund zählen Otto Hahn und Fritz Strassmann als die Entdecker der Kernspaltung und Lise Meitner und Otto Frisch als die ersten, die eine theoretische Erklärung für diesen Prozess bekannt gaben. Es war Otto Frisch, der die Bezeichnung Kernspaltung einführte. Otto Hahn hatte ursprünglich die Bezeichnung „Uranspaltung“ verwendet.
Bindungsenergie
Die Bindungsenergie eines Atomkerns ist abhängig von seiner Massenzahl A, also seiner Anzahl an Nukleonen (Protonen und Neutronen). Das bedeutet, dass Atome mit hohen Nukleonenzahlen (z. B. Uran-235) geringere Bindungsenergien haben als Atome mit einer niedrigeren Anzahl an Nukleonen (z. B. Barium-144 und Krypton-89).
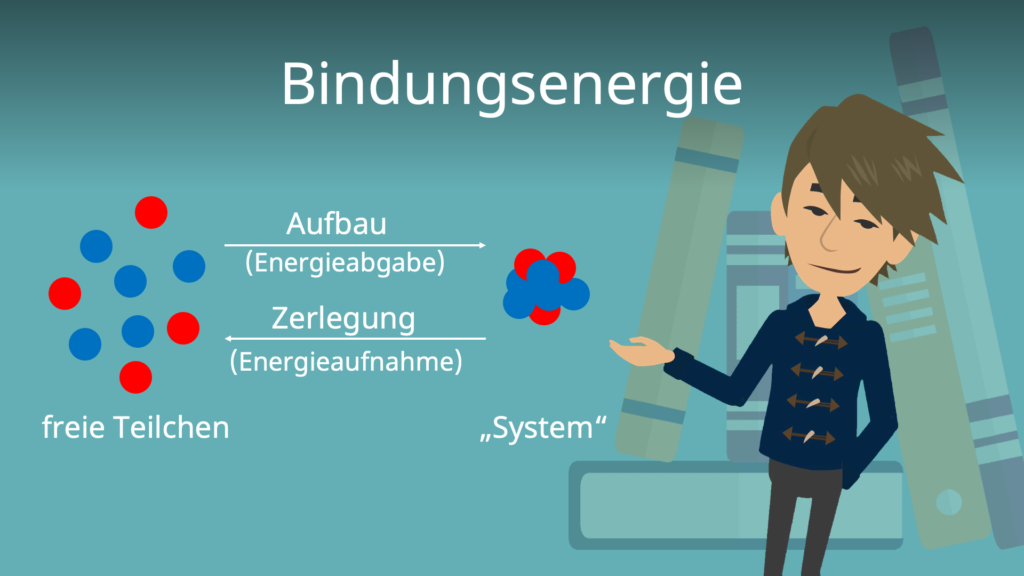
Wenn du versuchst einen Atomkern in seine einzelnen Bestandteile zu zerlegen, musst du dafür eine gewisse Arbeit aufwenden, denn zwischen den Nukleonen herrscht eine anziehende Kraft. Die Energie, die du aufwenden musst, um geradeso die anziehenden Kräfte auszugleichen, heißt Bindungsenergie.
Wenn du mehr über die Bindungsenergie, ihre Berechnung und ihre Einsatzgebiete erfahren möchtest, schau dir unser Video dazu an. Bis gleich!