LM Kurve
Dieser Artikel umfasst die Herleitung der LM Kurve und behandelt anschließend die Verschiebungen der LM Kurve, welche sich durch Veränderungen einzelner Variablen der LM Gleichung ergeben.
Du hast genug davon ausführliche Artikel über makroökonomische Theorien zu lesen und am Ende genauso viel zu wissen wie davor? Unser Video bereitet dem ein Ende und erklärt dir alles was du zur LM Kurve wissen musst!
Inhaltsübersicht
LM Kurve Definition
Die LM Kurve, auch bekannt als LM Gleichung oder LM Funktion, ist ein makroökonomisches Modell, welches aus dem Gleichgewicht zwischen Geldnachfrage und Geldangebot auf dem Geldmarkt abgeleitet wird.
LM Kurve Herleitung
Bevor wir die LM Kurve herleiten können, solltest du bereits über den Geldmarkt Bescheid wissen. Auf dem Geldmarkt, welcher ein Bestandteil des Finanzmarktes ist, stehen sich die kurzfristige Geldnachfrage und das kurzfristige Geldangebot gegenüber und legen zusammen den Geldmarktzins fest.
LM Kurve Erklärung
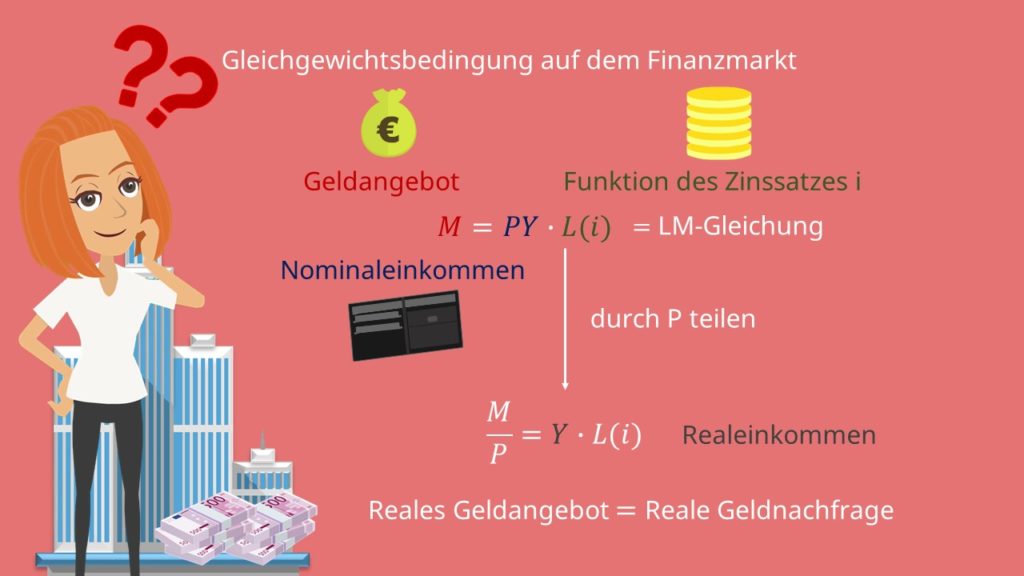
Die Buchstaben LM stehen für Liquidity preference-Money supply. Folglich beschreibt die LM Funktion wie sich die Geldnachfrage in Bezug zum Geldangebot ändert. Das Gleichgewicht auf dem Geldmarkt ist also Grundlage für die LM Kurve, welche neben der IS Kurve ein wichtiger Bestandteil des IS LM Modells ist. Für die Herleitung der LM Kurve wiederholen wir also zunächst die Gleichgewichtsbedingung auf dem Geldmarkt. Diese lautet:
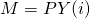
LM Kurve Formel
Eigentlich entspricht diese schon unserer Gleichung. Sie beschreibt den Zusammenhang zwischen Geldangebot, Nominaleinkommen und Zinssatz. Da wir uns aber bei der Analyse des Gleichgewichts auf das Realeinkommen konzentrieren, teilen wir diese Formel jetzt noch durch das Preisniveau 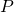 . Wir erhalten folgende Gleichung:
. Wir erhalten folgende Gleichung:
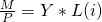
Somit steht auf der rechten Seite jetzt nicht mehr das Nominaleinkommen 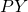 , sondern das Realeinkommen
, sondern das Realeinkommen 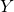 . Nach dieser Umstellung muss jetzt also das reale Geldangebot der realen Geldnachfrage entsprechen. Aber was ist eigentlich die reale Geldnachfrage?
. Nach dieser Umstellung muss jetzt also das reale Geldangebot der realen Geldnachfrage entsprechen. Aber was ist eigentlich die reale Geldnachfrage?
Stell dir vor, du möchtest dir jeden Tag in der Uni genau drei Butterbrezen kaufen. Wenn eine Brezen einen Euro kostet, musst du jeden Tag drei Euro Bargeld bei dir haben, um deine Brotzeit zu bezahlen. Der Wunsch nach drei Butterbrezen steht für deine reale Geldnachfrage. Dies entspricht deiner Nachfrage nach Bargeld ausgedrückt in Gütereinheiten.
LM Kurve berechnen
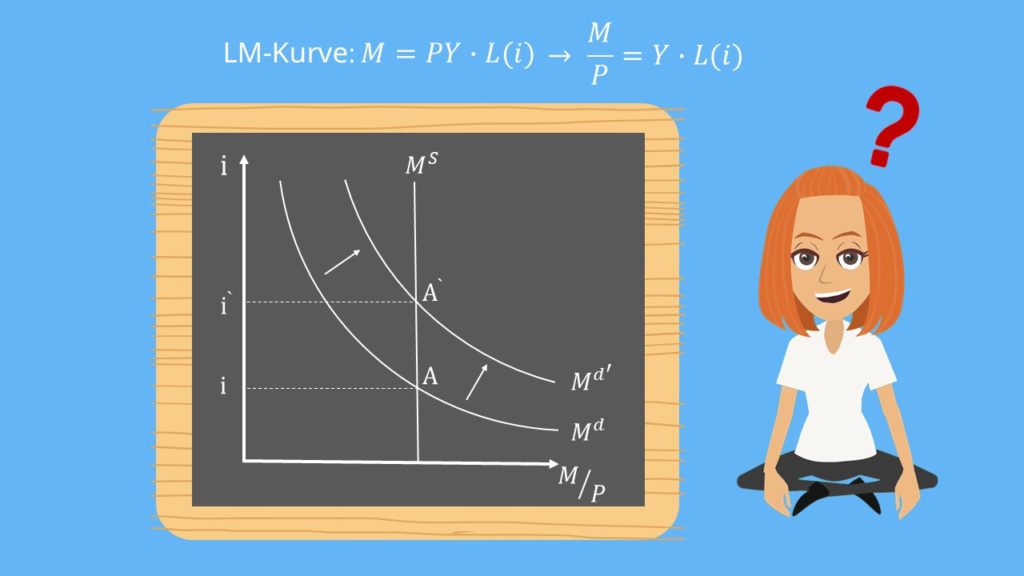
Die mathematische Funktion der Gleichung haben wir bereits hergeleitet. Um jetzt noch zu verstehen, wie man die LM Gleichung grafisch ableiten kann, schauen wir uns die Abbildung zum Gleichgewicht auf dem Geldmarkt an.
Hier steht 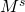 für das Geldangebot und
für das Geldangebot und 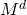 für die Geldnachfrage. Der einzige Unterschied ist, dass an der x-Achse nicht mehr die Geldmenge
für die Geldnachfrage. Der einzige Unterschied ist, dass an der x-Achse nicht mehr die Geldmenge 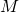 , sondern die reale Geldmenge
, sondern die reale Geldmenge 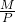 abgetragen ist. Im Gleichgewichtspunkt
abgetragen ist. Im Gleichgewichtspunkt 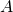 gilt Geldangebot gleich Geldnachfrage. Um daraus jetzt die LM Gleichung abzuleiten, müssen wir uns fragen was mit unserem Gleichgewicht passiert, wenn sich unser Einkommen
gilt Geldangebot gleich Geldnachfrage. Um daraus jetzt die LM Gleichung abzuleiten, müssen wir uns fragen was mit unserem Gleichgewicht passiert, wenn sich unser Einkommen 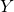 auf
auf 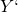 erhöht. Wenn wir mehr Lohn zur Verfügung haben, steigt logischerweise auch unsere Nachfrage nach Geld. Die Nachfragekurve
erhöht. Wenn wir mehr Lohn zur Verfügung haben, steigt logischerweise auch unsere Nachfrage nach Geld. Die Nachfragekurve 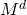 verschiebt sich also nach oben. Es stellt sich ein neues Gleichgewicht
verschiebt sich also nach oben. Es stellt sich ein neues Gleichgewicht 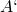 mit einem höheren Zinssatz ein. Bei gegebenem Geldangebot steigt also der Zinssatz mit zunehmendem Einkommen.
mit einem höheren Zinssatz ein. Bei gegebenem Geldangebot steigt also der Zinssatz mit zunehmendem Einkommen.
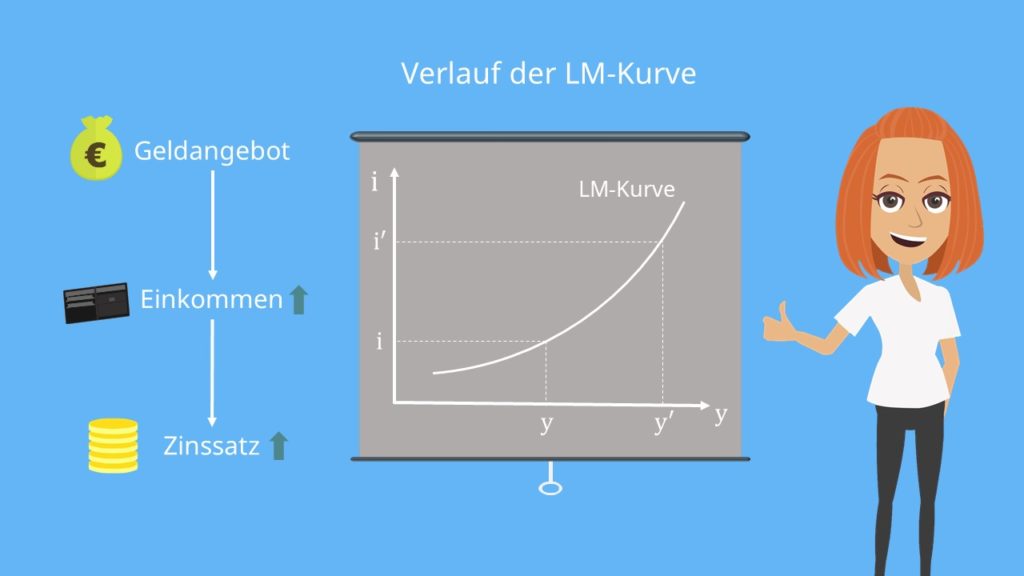
Daraus können wir jetzt den Verlauf der LM Funktion ableiten. Der positive Zusammenhang zwischen Zinssatz und Einkommen wird ganz einfach durch die positive Steigung der Kurve beschrieben.
LM Kurve Verschiebung
Jetzt weißt du, wie die Gleichung sowohl grafisch als auch mathematisch hergeleitet werden kann. Schauen wir uns als nächstes noch an, wie die LM Kurve verschoben wird. Allgemein lässt sich sagen, dass jede Veränderung der realen Geldmenge 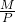 zu einer Verschiebung der Kurve führt. Stellen wir uns vor die Zentralbank verfolgt eine expansive Geldpolitik, sie entscheidet also die Geldmenge
zu einer Verschiebung der Kurve führt. Stellen wir uns vor die Zentralbank verfolgt eine expansive Geldpolitik, sie entscheidet also die Geldmenge 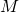 zu erhöhen.
zu erhöhen.
Welche Auswirkungen hat das auf das Gleichgewicht? Bei konstantem Preisniveau steigt das reale Geldangebot von 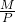 auf
auf 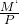 . Durch die höhere reale Geldmenge muss der Zinssatz bei gleichbleibendem Einkommen
. Durch die höhere reale Geldmenge muss der Zinssatz bei gleichbleibendem Einkommen 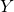 nun sinken, damit wieder ein Gleichgewicht existiert. Die LM Funktion verschiebt sich also nach unten. Auch bei einer Verringerung des Preisniveaus verschiebt sich die LM Kurve nach unten.
nun sinken, damit wieder ein Gleichgewicht existiert. Die LM Funktion verschiebt sich also nach unten. Auch bei einer Verringerung des Preisniveaus verschiebt sich die LM Kurve nach unten.
Gehen wir nun davon aus, dass die Zentralbank eine kontraktive Geldpolitik verfolgt, sie also die Geldmenge verringert. Hier würde folglich die reale Geldmenge 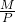 sinken. Um im Gleichgewicht zu bleiben, steigt der Zinssatz von
sinken. Um im Gleichgewicht zu bleiben, steigt der Zinssatz von 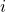 auf
auf 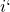 . Die Kurve verschiebt sich nach oben. Auch durch eine Erhöhung des Preisniveaus verschiebt sie sich wieder nach oben.
. Die Kurve verschiebt sich nach oben. Auch durch eine Erhöhung des Preisniveaus verschiebt sie sich wieder nach oben.