Hodges-Lehmann-Regel
Du hast schon von der Hodges-Lehmann-Regel gehört, weißt aber nicht wie du sie anwenden sollst? Kein Problem, in diesem Beitrag erklären wir dir wie du eine Entscheidung nach dieser Regel treffen kannst.
Inhaltsübersicht
Entscheidungen bei variabler Informationsstruktur
Bisher konnten wir jedem möglichen Zustand immer eine bestimmte Wahrscheinlichkeit zuordnen. Ab jetzt sind diese Wahrscheinlichkeitsverteilungen unsicher oder partiell, das heißt nur teilweise vorhanden. Nun dreht sich alles um Entscheidungen bei variabler Informationsstruktur, also Mischformen zwischen Sicherheit, Risiko und Ungewissheit.
1. Hodges-Lehmann-Regel
Eine Möglichkeit in dieser Situation eine Entscheidung treffen zu können, ist die Anwendung einer der beiden sogenannten Hodges-Lehmann-Regeln.
Betrachten wir zunächst die erste Hodges-Lehmann-Regel mit folgender Bewertungsfunktion:
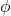 (ai) = l * Suij * pj + (1-l) * min uij → max
(ai) = l * Suij * pj + (1-l) * min uij → max
Diese ist quasi ein Kompromiss zwischen Bayes- und Wald-Regel. Indem wir diese beide Regeln jetzt kombinieren, erhalten wir eine Mischung aus Ungewissheit und Risiko. Mit dem Vertrauensparameter 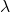 , der zwischen 0 und 1 liegen muss, können wir dann gewichten, welche der beiden Regeln wir stärker berücksichtigen wollen. Kompromisse zwischen anderen Regeln sind ebenso möglich.
, der zwischen 0 und 1 liegen muss, können wir dann gewichten, welche der beiden Regeln wir stärker berücksichtigen wollen. Kompromisse zwischen anderen Regeln sind ebenso möglich.
Betrachten wir das ganze anhand eines Beispiels. Stell dir vor du stehst vor folgendem Entscheidungsproblem:
Um die Wahrscheinlichkeiten der einzelnen Zustände zu erfahren, hast du einen Experten um Hilfe gebeten. Dieser hat dir für Zustand 1 und 2 eine Wahrscheinlichkeit von je 30% und für Zustand 3 eine Wahrscheinlichkeit von 40% prognostiziert. Allerdings kannst du seinen Angaben nicht ganz vertrauen, weil er sich aufgrund eines Alkoholproblems des Öfteren verrechnet.
Deswegen, und weil du generell eher pessimistisch bist, möchtest du nicht nur die Bayes-Regel anwenden, bei der man sich nur auf die Erwartungswerte verlässt, sondern auch das Minimax-Prinzip. Dafür ist die 1. Hodges-Lehmann-Regel eine ideale Lösung. Als Vertrauensparameter 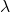 legst du einen Wert von 0,5 fest.
legst du einen Wert von 0,5 fest.
Und wie rechnet man nun weiter? In unserem Video erklären wir es dir!