Grundmodell der Entscheidungstheorie
Du arbeitest als Praktikant an der Wall Street und sollst jetzt entscheiden in welche von den drei möglichen Aktien investiert werden soll, hast aber keine Ahnung wie das geht? In diesem Beitrag zeigen wir dir, wie du dich am besten entscheidest!
Inhaltsübersicht
Aktionen als Wahlalternativen
Um sich für die bestmögliche Investition zu entscheiden, müssen wir erstmal ein Grundmodell aufstellen. Du hast die Wahl zwischen drei möglichen Aktien: Aktie 1, Aktie 2 und Aktie 3. In unserem Modell heißen diese verschiedenen Alternativen „Aktionen“ und werden als kleines a notiert.
Entscheidung nach dem Ausschöpfungsprinzip [[ jump_to-video 01:03 ]]
Die Möglichkeit in Aktie 1 zu investieren entspricht also a1, a2 bedeutet wir stecken Geld in Aktie 2 und a3 steht dafür in Aktie 3 zu investieren. Jetzt haben wir unseren sogenannten Aktionenraum festgelegt, aus dem wir uns gemäß dem Ausschöpfungsprinzip für eine Alternative entscheiden müssen. Er wird so notiert: A={a1,a2,a3}.
Allerdings betrachten wir in unserem Modell nicht nur verschiedene mögliche Aktionen, sondern auch unterschiedliche Zustände. Immerhin entscheidest du dich nicht willkürlich für eine Aktion, sondern für diejenige mit dem höchsten Gewinn. Gehen wir davon aus, du planst eine Investition für die nächsten 2 Jahre. Dann entsprechen die Zustände einfach den verschiedenen Jahren. z0 entspricht unserem aktuellen Jahr, z1 beschreibt den Zustand in einem Jahr und z3 den Zustand in 2 Jahren. Wie auch bei den Aktionen können wir jetzt unseren Zustandsraum definieren: Z={z0,z1,z2}.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Aufstellen der Ergebnismatrix [[ jumt_to_video 01:49 ]]
Da wir jetzt sowohl unsere verschiedenen Aktionen als auch unsere Zustände definiert haben, können wir unsere Ergebnismatrix aufstellen.
Aktion 1: in Aktie 1 investieren Zustand 0 = Jahr 0
Aktion 2: in Aktie 2 investieren Zustand 1 = Jahr 1
Aktion 3: in Aktie 3 investieren Zustand 2 = Jahr 2
In dieser Matrix kannst du sehen, wie sich deine 3 Aktionen in den nächsten 2 Jahren entwickeln. Damit wir nun aber bewerten können, in welche Aktie du optimalerweise investieren solltest, müssen wir aus dieser Ergebnismatrix eine sogenannte Entscheidungsmatrix machen. Man unterscheidet 3 Arten von Entscheidungsmatrizen: die Nutzenmatrix, die Schadensmatrix und die Opportunitätskostenmatrix. Für unser Beispiel verwenden wir jetzt die am häufigsten gebrauchte Nutzenmatrix.
Umwandlung in die Nutzenmatrix
Um die Ergebnismatrix in eine Nutzenmatrix zu verwandeln brauchen wir als erstes eine Nutzenfunktion u(x). Gehen wir mal davon aus, dass du 50% des Gewinns aus den Investitionen an die Bank abgeben musst. Somit lautet deine Nutzenfunktion u(x)=0,5x. Dann nehmen wir an, dass der Nutzen, den du aus den Investitionen ziehst, genau der Hälfte der Renditen entspricht, den sie abwerfen. Unsere Nutzenmatrix sieht also so aus:
Anwendung des Dominanzprinzips
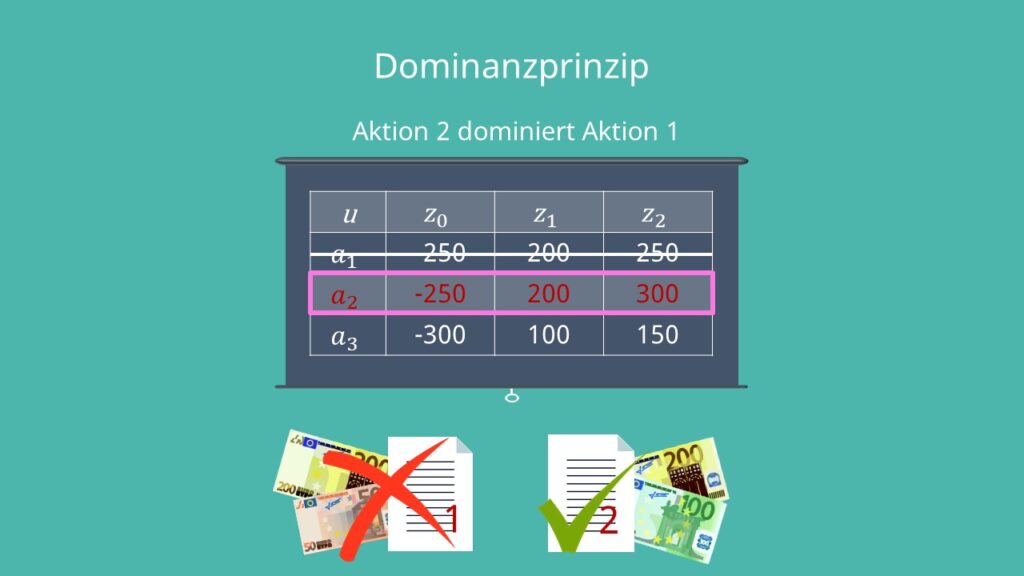
Aber in welche Aktie solltest du nun investieren? Um das herauszufinden, wendet man in der Entscheidungstheorie das sogenannte Dominanzprinzip an. Dabei vergleichst du einfach die Werte der einzelnen Aktionen in jedem Zustand miteinander. Vergleichen wir zunächst Aktion 1 mit Aktion 2. Wie du siehst, weisen die Aktien in den ersten beiden Jahren genau die gleichen Renditen auf. Da im Jahr 2 die Aktie 2 jedoch eine höhere Rendite abwirft als die Aktie 1, ist diese zu bevorzugen.
Aktie 2 performt also in jedem Jahr gleich gut oder besser als Aktie 1. In der Entscheidungstheorie sagen wir dazu: Aktion 2 dominiert Aktion 1. Somit können wir Aktion 1 jetzt streichen, da wir Aktion 2 in jedem Fall vorziehen.
Jetzt müssen wir noch Aktion 2 und Aktion 3 vergleichen. Wie du siehst, performt Aktie 2 wieder in jedem Jahr besser als Aktie 3. Da Aktion 3 dominiert wird, können wir diese wiederum streichen.
Aktion 2 ist folglich dominant gegenüber den anderen Aktionen. Aktion 2 ist somit effizient oder pareto-optimal . Es ist also die beste Entscheidung in Aktie 2 zu investieren.
Jetzt hast du das Grundmodell der Entscheidungstheorie verstanden und kannst auch noch deinen Chef mit deiner guten Entscheidung beeindrucken!