Phillipskurve
Dieser Artikel behandelt die Phillipskurve. Nach der Definition und Erklärung wird die Formel der erweiterten Phillipskurve hergeleitet und interpretiert. So wird der negative Zusammenhang zwischen der Inflationsrate und der Arbeitslosenquote deutlich.
Du hast es satt dir mühsam alles durchlesen zu müssen? Musst du nicht! Unser Video fasst dir den Artikel zusammen und vermittelt dir alles was du zur Phillipskurve wissen musst einfach und verständlich in wenigen Minuten.
Inhaltsübersicht
Definition Phillipskurve
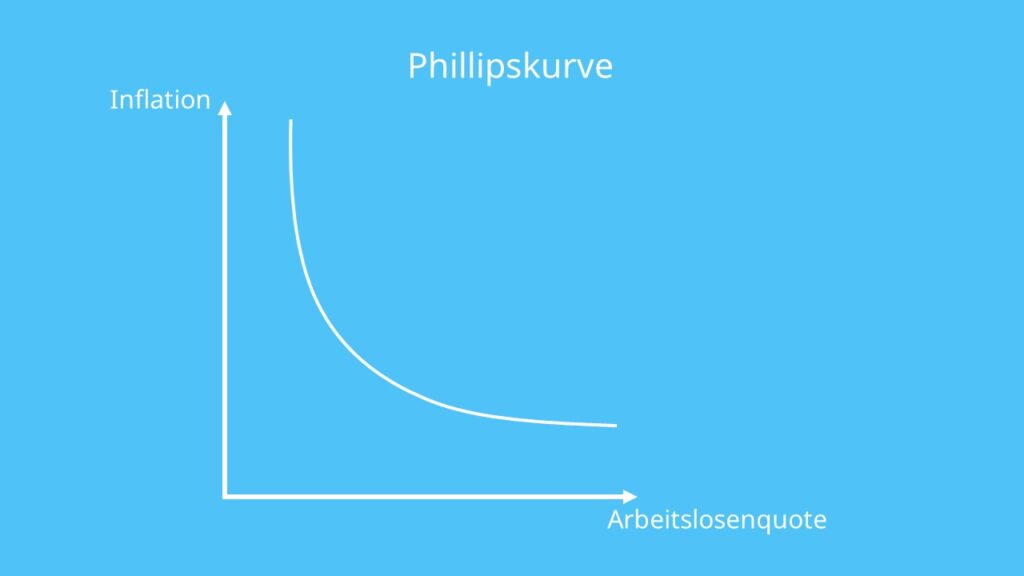
Die Phillipskurve geht auf den Ökonom Alban Phillips zurück, welcher ursprünglich den Zusammenhang zwischen Lohnänderungen und Preissteigerungen auf der einen Seite und der Arbeitslosenquote auf der anderen Seite beschrieb. Heutzutage gibt die erweiterte Phillipskurve den negativen Zusammenhang zwischen der Inflationsrate und der Arbeitslosenquote wieder.
Modifizierte Phillipskurve
Die 1958 von Phillips erstellte Kurve bildet auf der y-Achse die Zuwachsrate des Nominallohns und auf der x-Achse die Arbeitslosenquote ab und stellt so den Zusammenhang zwischen diesen beiden Größen dar. Um der Phillipskurve mehr wirtschaftliche Relevanz zu geben, erstellten 1960 Samuelson und Solow die erweiterte Phillipskurve und tauschten die Größe an der y-Achse aus. Die modifizierte Phillipskurve, beschreibt die Beziehung zwischen der von den Marktteilnehmern erwarteten Inflationsrate und der Arbeitslosenquote.
Phillipskurve Erklärung
Zwischen den beiden volkswirtschaftlichen Indikatoren der Inflationsrate und der Arbeitslosenquote besteht ein negativer Zusammenhang. Das bedeutet, dass bei einem Anstieg der Inflationsrate die Arbeitslosenquote im Gegenzug sinkt. Diese Beziehung wird durch eine fallende Gerade, also die erweiterte Phillipskurve abgebildet. Auch heute noch findet die modifizierte Phillipskurve in der Praxis Anwendung, beispielsweise bei dem Versuch die Ziele der Wirtschaftspolitik zu realisieren. Hierbei liegt ein besonderer Fokus auf der Arbeitslosenquote und der Inflationsrate, welche Bestandteile des magischen Vierecks sind.
Phillipskurve Formel
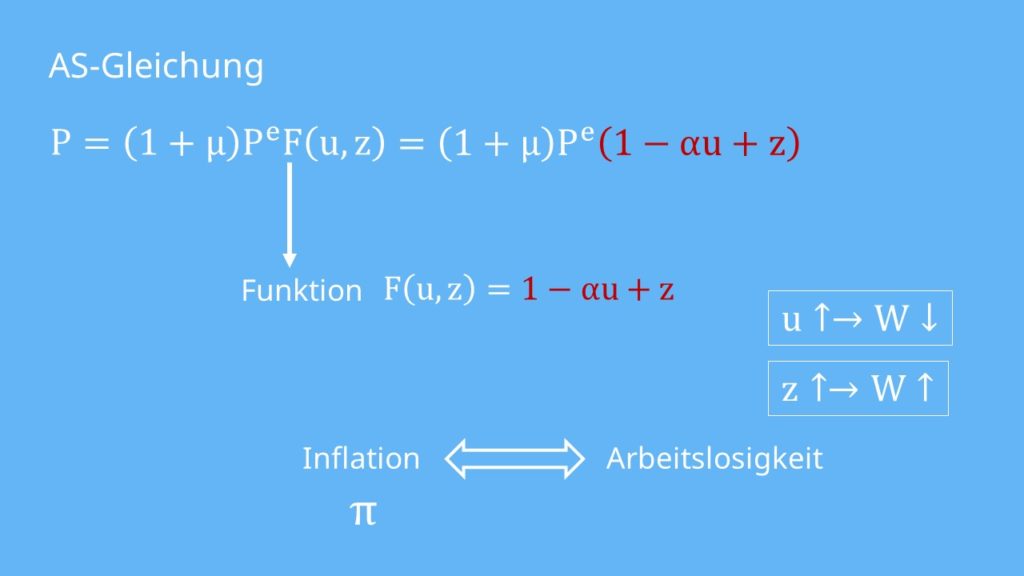
Zunächst erinnern wir uns nochmal an die Gleichung der AS-Kurve:
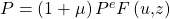
Bisher haben wir die Funktion 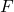 nicht ausgeschrieben. Um uns der Phillippskurve anzunähern, wollen wir das jedoch ändern. Die spezifische Form, die wir für die weiteren Überlegungen wählen, sieht folgendermaßen aus:
nicht ausgeschrieben. Um uns der Phillippskurve anzunähern, wollen wir das jedoch ändern. Die spezifische Form, die wir für die weiteren Überlegungen wählen, sieht folgendermaßen aus:
Du erinnerst dich sicher an die Zusammenhänge der AS-Kurve. Je höher die Erwerbslosenquote 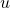 , desto niedriger ist der Lohn. Und je größer unser Wert für
, desto niedriger ist der Lohn. Und je größer unser Wert für  ist, desto höher ist der Lohn. Genau das wird also durch diese Formel abgebildet. Setzen wir die ermittelte Darstellung in die AS-Gleichung ein, erhalten wir:
ist, desto höher ist der Lohn. Genau das wird also durch diese Formel abgebildet. Setzen wir die ermittelte Darstellung in die AS-Gleichung ein, erhalten wir:
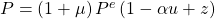
Phillipskurve Ableitung Inflationsrate
Und genau daraus können wir einen Zusammenhang für die Inflationsrate 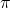 ableiten, die wir für die Phillipskurve benötigen. Wir ersparen dir an dieser Stelle aber die komplizierte Umformung und kommen direkt zu der Gleichung, die unsere Inflation abbildet:
ableiten, die wir für die Phillipskurve benötigen. Wir ersparen dir an dieser Stelle aber die komplizierte Umformung und kommen direkt zu der Gleichung, die unsere Inflation abbildet:
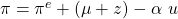
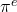 ist dabei die erwartete Inflationsrate und
ist dabei die erwartete Inflationsrate und 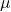 unser bekannter Preisaufschlag. Und damit hast du auch schon fast die Grundform der Philips Kurve kennengelernt. Du solltest dabei – wie beim AS-AD-Modell – verstehen, wie sich Veränderungen der Parameter auf die Gleichung auswirken. Was passiert beispielsweise bei einem Anstieg der erwarteten Inflation
unser bekannter Preisaufschlag. Und damit hast du auch schon fast die Grundform der Philips Kurve kennengelernt. Du solltest dabei – wie beim AS-AD-Modell – verstehen, wie sich Veränderungen der Parameter auf die Gleichung auswirken. Was passiert beispielsweise bei einem Anstieg der erwarteten Inflation 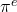 ? Dafür betrachten wir nochmal die AS-Gleichung und erinnern uns was passiert, wenn sich die Preiserwartung
? Dafür betrachten wir nochmal die AS-Gleichung und erinnern uns was passiert, wenn sich die Preiserwartung 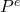 erhöht. In der Formel erkennst du sofort, dass dadurch zwangsweise auch das tatsächliche Preisniveau anwächst.
erhöht. In der Formel erkennst du sofort, dass dadurch zwangsweise auch das tatsächliche Preisniveau anwächst.
Und damit haben wir den gewünschten Zusammenhang schon hergestellt. Die Inflation ist nämlich definiert als ein Anstieg des Preisniveaus. Für die Arbeitslosenquote, den Preisaufschlag und die Sammelvariable gelten die analogen Zusammenhänge wie beim Preisniveau, die sich aus der Formel auch schon ablesen lassen:
Typischerweise wird die Gleichung der Inflation jetzt noch mit Zeitindizes versehen und schon haben wir unser Ziel erreicht. Entscheidend ist dabei, dass die Variablen 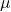 und
und  keinen Index bekommen, da diese als gegeben angenommen werden. Für unsere Gleichung ergibt sich damit:
keinen Index bekommen, da diese als gegeben angenommen werden. Für unsere Gleichung ergibt sich damit:
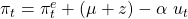
Nun können wir die Phillipskurve auch noch graphisch darstellen.
Phillipskurve Berechnung
Wir können uns dieses Wissen jetzt zu Nutze machen, um beispielsweise die natürliche Arbeitslosenquote zu berechnen. Du erinnerst dich, dass diese Quote genau dann gegeben ist, wenn das erwartete Preisniveau dem tatsächlichen Preisniveau entspricht. Analog dazu nehmen wir jetzt an, dass es sich bei der erwarteten und der tatsächlichen Inflation genauso verhält. Ist die Phillipskurve beispielsweise gegeben mit:
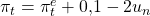
können wir die beiden Ausdrücke 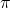 für die Inflation direkt streichen, da diese genau den gleichen Wert annehmen. Das
für die Inflation direkt streichen, da diese genau den gleichen Wert annehmen. Das 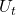 haben wir hier schon direkt mit dem
haben wir hier schon direkt mit dem 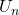 der natürlichen Arbeitslosenquote ersetzt. Damit erhalten wir dann:
der natürlichen Arbeitslosenquote ersetzt. Damit erhalten wir dann:
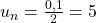
Die natürliche Arbeitslosenquote ist also 5 Prozent.