Gaskonstante

Gaskonstante Definition

Die Gaskonstante ist eine Proportionalitätskonstante, die hauptsächlich in der Thermodynamik verwendet wird. Diese kann unter anderem auch als universelle Gaskonstante, allgemeine Gaskonstante, ideale Gaskonstante oder molare Gaskonstante bezeichnet werden. Sie stellt einen wichtigen Teil zur Beschreibung eines idealen Gases für die allgemeine Gasgleichung dar.

Im Jahr 1811 führte der italienische Physiker und Chemiker Amadeo Avogadro empirisch Experimente durch. Dadurch stellte er fest, dass die Gaskonstante für alle idealen Gase denselben Wert besitzt. Diese Regel wurde bekannt als das „Gesetz von Avogadro“.

Merke

Die Gaskonstante findet nicht nur in der allgemeinen Gasgleichung Anwendung, sondern auch in anderen thermodynamischen Zusammenhängen. So tritt sie zum Beispiel bei der molaren Wärmekapazität () oder zur Beschreibung der inneren Energie () eines idealen Gases auf.

Der Artikel Fundamentalgleichungen der Thermodynamik beschreibt die Bedeutung und die Anwendung der inneren Energie näher.

Ideales Gas

Ein ideales Gas besteht aus sehr kleinen Teilchen, weshalb die Größe dieser Teilchen vernachlässigt werden kann. Sie können sich frei in einem definierten Volumen bewegen. Unter diesen Teilchen wirken keine Kräfte, jedoch kommt es zu elastischen Stößen zwischen den Teilchen untereinander und mit der Wand des Volumens. Wenn sich ein Teilchen geradlinig mit einer konstanten Geschwindigkeit bewegt, dann kann ein elastischer Stoß das Teilchen in eine andere Richtung lenken und dabei beschleunigen oder abbremsen.

direkt ins Video springen

Da jedoch zwischen unterschiedlichen Gasteilchen immer Kräfte herrschen, ist das ideale Gas nur eine Modellvorstellung. Wenn aber keine Stöße der Teilchen zugelassen werden würden, könnte man das Gas nicht in ein Volumen einsperren, da es die Wand nicht bemerken würde. Es ist also notwendig, dass das thermodynamische System geschlossen ist.

Außerdem würden die Teilchen dann die Anfangsgeschwindigkeit beibehalten. Somit wäre das System nicht in einem thermodynamischen Gleichgewicht, weshalb die thermodynamischen Hauptsätze hier nicht gelten würden.

Im Artikel Thermodynamische Systeme und Zustandsgrößen werden offene, geschlossene und isolierte Systeme beschrieben und voneinander abgegrenzt.

Gaskonstante berechnen

Die allgemeine Gaskonstante ist das Produkt aus der sogenannten Avogadro Konstante  und der Boltzmann Konstante  und wird durch den Buchstaben 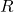beschrieben.

Die Avogadro Konstante gibt die Anzahl der Teilchen in einem Mol an, was genau Teilchen entspricht. Diese Teilchen nehmen unter Normalbedingungen, also einer Temperatur von 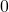Grad Celsius und einem Druck von , mit der Einheit Pascal, ein Volumen von ca. ein.

Mit der Boltzmann Konstante kann beschrieben werden, wie viel Energie ein Teilchen pro Kelvin besitzt. Mit ihr kann also zwischen absoluter Temperatur und Energie umgerechnet werden.

Gaskonstante Einheit

Durch Einsetzen der Avogadro und der Boltzmann Konstante erhalten wir die ideale Gaskonstante R als:

Meist genügt für die Konstante R ein gerundeter Wert von:

Spezifische Gaskonstante

Abgeleitet davon ergibt sich die sogenannte spezifische Gaskonstante . Diese ist auch unter dem Namen individuelle Gaskonstante oder spezielle Gaskonstante bekannt. Dadurch kann durch Hinzunahme einer stoffspezifischen Größe, der molaren Masse, das 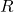für jedes ideale Gas berechnet werden.

Spezifische Gaskonstante R Luft

Um die von Luft zu berechnen, wird zuerst die molare Masse von Luft benötigt. Die molare Masse von trockener Luft beträgt . Somit ergibt sich die als:

Spezifische Gaskonstante Beispiel

Die spezielle Gaskonstante kann in der idealen Gasgleichung verwendet werden, um deren unterschiedliche Größen zu berechnen.

In dem Artikel Thermodynamische Zustandsgrößen und Grundgleichungen wird näher auf die ideale Gasgleichung eingegangen.

Zum besseren Verständnis ein Beispiel:

Ein mit Helium befülltes Gefäß besitzt ein Volumen von und es herrscht ein Druck von MegaPascal. Wie groß ist die Masse des Gases bei einer Temperatur von Grad Celsius?

Zunächst muss die Temperatur von Grad Celsius in Kelvin umgewandelt werden. Dazu wird auf den Celsius Wert die Zahl addiert:

Für Helium, das eine Molare Masse von ca. besitzt, ergibt sich zu:

Bekannt ist uns schon der thermodynamische Zusammenhang der Stoffmenge mit der Masse und der molaren Masse:

Dieser Zusammenhang wird im Artikel Thermodynamische Zustandsgrößen genauer betrachtet.

Außerdem lässt sich aus der Gleichung für die spezifische Gaskonstante folgende Gleichung umformen:

Diese Zusammenhänge können in die allgemeine Gasgleichung  eingesetzt werden. So lässt sich diese umschreiben zu:

.

Durch Umformen entsteht der Zusammenhang:

Somit müssen die Werte nur noch eingesetzt werden und es ergibt sich eine Masse des Gases von: