Der 1. Hauptsatz der Thermodynamik
Du möchtest mehr wissen über die Energieerhaltung in thermodynamischen Systemen und den ersten Hauptsatz der Thermodynamik besser verstehen? Dann bist du hier genau richtig!
Inhaltsübersicht
Besondere Form des Energieerhaltungssatz: Der erste Hauptsatz der Thermodynamik
Schon immer haben Erfinder versucht, Maschinen zu entwerfen, die mehr Energie liefern, als man dem System zuführt. In diesem Fall könnten sie fortwährend laufen und damit konstant Energie abgeben.
Leider ist dies nur in der Theorie möglich, da es dem 1. Hauptsatz der Thermodynamik widerspricht.
Dieser besagt, dass in einem geschlossenen System die Änderung ΔU der inneren Energie des Systems gleich der mit der Umgebung ausgetauschten Wärme Q und Arbeit W ist.
Der 1. Hauptsatz der Thermodynamik ist also eine besondere Form des Energieerhaltungssatzes. Es ist nicht möglich dabei neue Energie zu erzeugen oder Energie zu vernichten. Für den Übergang eines geschlossenen Systems von Zustand A nach B lautet der 1. Hauptsatz der Thermodynamik:
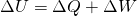
Die Zunahme der inneren Energie ist gleich der Summe der einem System von außen zugeführten Wärme und zugeführten Arbeit.
Dazu sollte man fairerweise sagen, dass diese Aussage nicht beweisbar ist und wie der Energieerhaltungssatz auf reinen Erfahrungswerten basiert.
Erklärung des 1. Hauptsatz anhand eines Beispiels
Schauen wir uns zur Verdeutlichung doch mal ein Beispiel an:
Stell dir einen Zylinder vor in dem Wasserstoff durch eine Scheibe eingeschlossen wird. Der Druck, der von der Scheibe auf den Wasserstoff ausgeübt wird, lässt sich ganz einfach durch die Formel Kraft pro Fläche ermitteln.
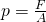
Wenn die Scheibe ruht, stehen die Systeme im Gleichgewicht und der Druck des eingeschlossenen Wasserstoffs ist genauso groß, wie der Druck von außen.
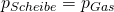
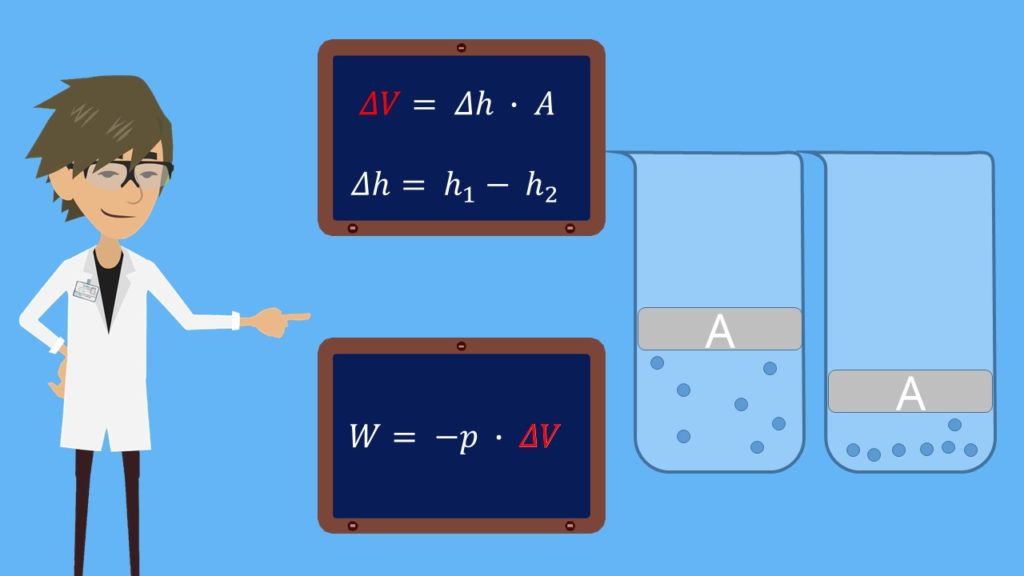
Wenn wir nun das Gewicht der Scheibe erhöhen, komprimieren wir den eingeschlossenen Wasserstoff. Dies geschieht solange bis wieder ein Gleichgewicht zwischen Druck und Gegendruck besteht. Wir haben nun Arbeit W am System verrichtet, welche sich definiert als:
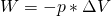
Dabei ist p wieder der Druck und die Volumenänderung des Gases. Die Volumenänderung des Gases erhält du, wenn du die Fläche A mit der Höhenänderung des eingeschlossenen Gasvolumens multiplizierst:
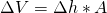
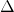 h ist dabei die Differenz der beiden Höhen des Gases.
h ist dabei die Differenz der beiden Höhen des Gases.
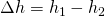
Wenn sich der Kolben nach unten bewegt, wird das Volumen des Gases verringert. Daraus folgt, dass bei positivem h die Volumenänderung negativ ist, da das Gas komprimiert wurde.
Dass die verrichtete Arbeit positiv sein muss, erkennst du auch, wenn du die negative Volumenänderung in die erste Formel einsetzt.
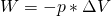
Enthalpie und innere Energie
Fassen wir doch das Ganze noch einmal zusammen:
Bei idealen Gasen wird die Arbeit, die das System bei infinitesimaler Expansion um ΔV gegen den äußeren Druck p leistet, durch die Formel
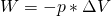
definiert.
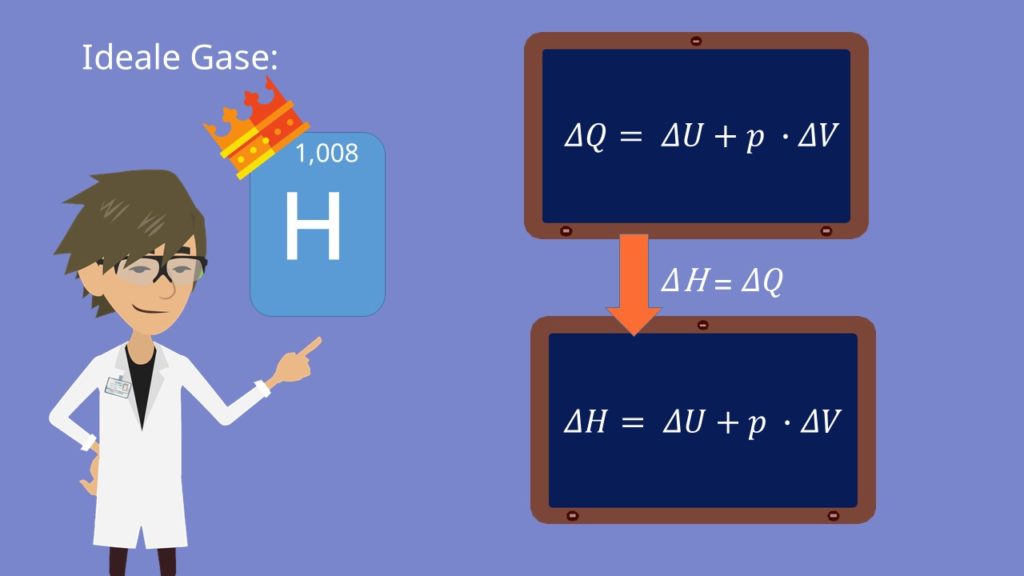
Daraus können wir den ersten Hauptsatz für ein ideales Gas ableiten:
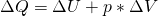
Stellen wir diese Formel nach 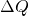 um, erhalten wir:
um, erhalten wir:
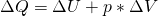
In diesem Fall entspricht die Enthalpieänderung 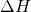 der Wärmemenge
der Wärmemenge 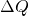
Denn aus der Definition der Enthalpie wissen wir, dass die Enthalpie H der Inneren Energie U plus der Volumenarbeit p mal V entspricht:
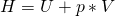
Du kannst dir auch gerne unser Video zur Enthalpie anschauen, wenn du dir an dieser Stelle nicht mehr ganz sicher bist, was es damit auf sich hat.
Das gilt aber nur in einem geschlossenen isobaren System bei dem lediglich Volumenarbeit verrichtet wird. Demnach können wir 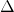 Q durch
Q durch 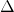 H ersetzen und erhalten:
H ersetzen und erhalten:
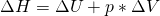
Bei einer exothermen Reaktion nimmt die Enthalpie des Systems ab. Demnach ist 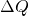 beziehungsweise
beziehungsweise 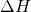 negativ. Umgekehrt ist
negativ. Umgekehrt ist 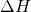 positiv, wenn es zu einer Wärmeaufnahme kommt und die Reaktion endotherm ist.
positiv, wenn es zu einer Wärmeaufnahme kommt und die Reaktion endotherm ist.
So, nun weißt du warum in einem geschlossenen System die Änderung der inneren Energie gleich der mit der Umgebung ausgetauschten Wärme ist. Viel Erfolg!