Entropie – Definition
Die Entropie ist eine physikalische Größe in der Chemie. Was die Bedeutung von Entropie ist und wieso viele den Begriff Unordnung mit ihr verbinden, erklären wir dir hier oder im Video.
Inhaltsübersicht
Was ist Entropie?
Die Entropie ist genauso wie der Druck und die Temperatur eine Zustandsgröße. Dementsprechend ist sie in der Thermodynamik wichtig, um ein System zu beschreiben. Ihr Formelzeichen lautet S.
Entropie wird häufig als Unordnung verstanden. Darunter kannst du dir folgendes vorstellen: Durch verschiedene Anordnungsmöglichkeiten von Teilchen in einem System steigt das Maß der Unordnung und somit auch die Entropie.
Entropie Bedeutung
Einfach erklärt bedeutet die Zunahme von Entropie eine erhöhte Unordnung im System. In den meisten Fällen steigt die Entropie an, wenn die Ordnung kleiner und die Unordnung größer wird.
Wenn du beispielsweise Parfüm in die Luft sprühst, befinden sich die Gasteilchen („Parfümwolke“) kurz danach in deiner Nähe. Nach einigen Minuten sind sie jedoch gleichmäßig in der Luft verteilt. Denn Systeme streben durch größere Unordnung — hier Verteilung der Gasteilchen — eine Zunahme der Entropie an.
Weiterhin kannst du mit Hilfe der Änderung der Entropie abschätzen, ob chemische Reaktionen und andere Prozesse spontan ablaufen können.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Entropie Definition
Die erste Definition der Entropie stammt von Ludwig Boltzmann. Er definierte die Entropie als Maß für die Anordnungsmöglichkeiten von Teilchen.
Entropie nach Boltzmann
Die erste Beschreibung der Entropie erfolgte im 19. Jahrhundert. Dabei betrachtete Boltzmann Teilchen einer Flüssigkeit oder eines Gases in einem abgeschlossenen System. Hier sind das Volumen V und die Teilchenzahl N konstant.
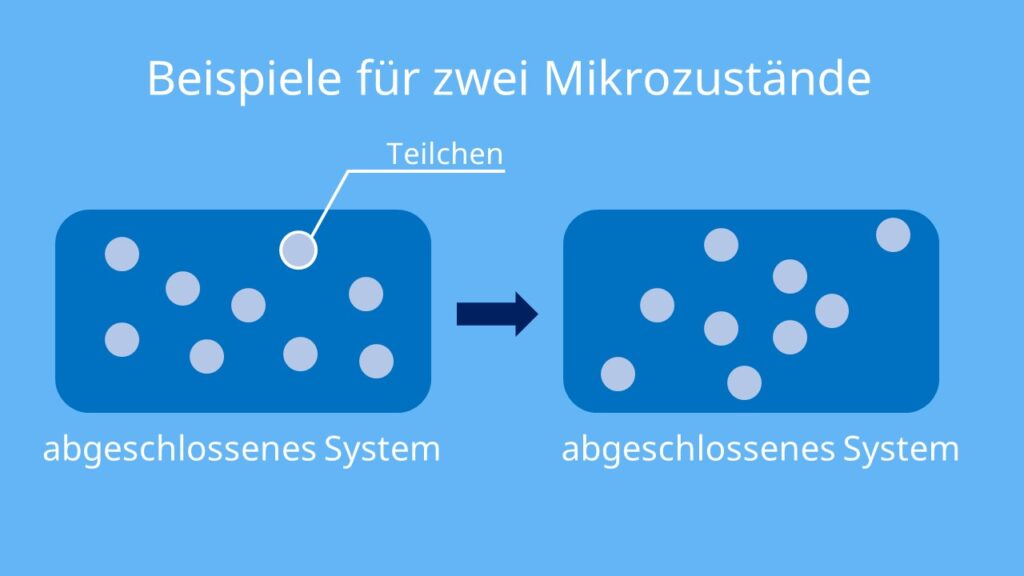
Die Teilchen in einem abgeschlossenen System können sich unterschiedlich anordnen. Deshalb unterschied Boltzmann zwischen verschiedenen Zuständen der Teilchenanordnung. Er nannte sie Mikrozustände.
Es gilt: Je unterschiedlicher sich die Teilchen im System anordnen können, desto größer ist die Anzahl der Mikrozustände. Je größer die Anzahl der Mikrozustände, desto größer die Entropie.
Entropie und Unordnung
Daraus folgte Boltzmanns Definion der Entropie als Maß für die Anordnungsmöglichkeiten der Teilchen. Der Begriff Unordnung ist hierbei etwas irreführend, da Teilchen im flüssigen und gasförmigem Zustand im Teilchenmodell keiner regelmäßigen Ordnung unterliegen.
Ein passendes Beispiel für den Begriff Unordnung ist das Schmelzen eines Kristalls. Denn im festen Kristall haben die Atome eine hohe Ordnung (Kristallgitter). Beim Schmelzprozess verlassen die Teilchen ihre festen Plätze, wodurch die Entropie steigt.
Entropie berechnen
Boltzmann stellte für seine Betrachtungen eine Formel für die Entropie S auf. Damit kannst du sie berechnen.

kB steht hier für die Boltzmann-Konstante und w für die Wahrscheinlichkeit eines Makrozustandes. Die Entropie ist demnach proportional zu der Wahrscheinlichkeit.
Weiterhin gibt dir die Formel der Entropie auch direkt ihre Einheit. Da der Logarithmus keine Einheit hat, entspricht die Einheit der Entropie S der Einheit der Boltzmann-Konstante.
Die Einheit der Entropie ist Joule (J) pro Kelvin (K), das bedeutet Energie pro Temperatur.
Den Unterschied zwischen Mikro– und Makrozustand erläutern wir dir an einem Beispiel.
Makrozustand und Mikrozustand
Stell dir ein Kristallgitter mit fünf freien Plätzen vor. Du kannst auf diese Plätze nun ein bis fünf Atome verteilen. Dabei erhältst du fünf verschiedene Makrozustände. Sie sind durch die Anzahl der freien Plätze und die Anzahl der Atome, die du verteilen kannst (1-5), definiert.
Die Anzahl der Mikrozustände erhältst du nun durch die verschiedene Anordnung der Atome in einem Makrozustand. In dem Makrozustand mit einem Atom kann es jede Stelle im Kristallgitter besetzen, woraus fünf Mikrozustände folgen.
Wir betrachten in unserem Beispiel den einfachen Fall. Hierbei spielt die Reihenfolge der Atome keine Rolle. Demnach hat der Makrozustand fünf nur einen Mikrozustand, da die Atome sich nur auf eine Weise anordnen können.
Entropie in der Thermodynamik
In der Thermodynamik ist die Entropie S eine Zustandsgröße. Sie steht mit anderen Zustandsgrößen wie der Enthalpie H und der Gibbs-Energie G in einem Zusammenhang. Er wird durch folgende Gleichung beschrieben:

Weiterhin gilt für die Entropie in abgeschlossenen Systemen, dass sie nicht abnehmen kann. Sie bleibt entweder konstant oder steigt (ΔS≥0). Du bezeichnest das auch als den zweiten Hauptsatz der Thermodynamik .
Rudolf Clausius beschrieb die Entropieänderung als Verhältnis von Wärmeänderung (ΔQ) und absoluter Temperatur T:

Dabei bezeichnet ΔQ eine kleine, dem System reversibel zugeführte Wärmemenge und T die Temperatur, die dabei herrscht. Die Formel besagt, dass bei Wärmeübertragung auch immer eine Entropieübertragung stattfindet.
Entropie chemische Reaktion
Im Zusammenhang chemischer Reaktionen kannst du auch eine Entropieänderung beobachten. Dabei kann sie sowohl positiv (ΔS>0) als auch negativ (ΔS<0) sein. Einfache Indikatoren für die Erhöhung der Entropie bei chemischen Reaktionen sind:
- größere Teilchenzahl bei den Produkten gegenüber den Edukten
- Bildung von Flüssigkeiten und Gasen als Produkte
Weiterhin kannst du bei einer chemischen Reaktion eine Aussage darüber treffen, ob sie freiwillig abläuft oder nicht. Das sagt dir nämlich die Änderung der Gibbs-Energie (ΔG):
- negative Gibbs-Energie (ΔG<0) –> Reaktion läuft freiwillig ab
- positive Gibbs-Energie (ΔG>0) –> Reaktion läuft nicht freiwillig ab
Dazu musst du jedoch die Änderung der Reaktionsenergie (ΔE) sowie die Entropieänderung (ΔS) kennen.

Du unterscheidest dabei zwischen vier verschiedenen Fällen:
| Entropieänderung positiv: ΔS>0 | Entropieänderung negativ: ΔS<0 | |
| Exoth. Reaktion: ΔE<0 |
ΔE negativ TΔS negativ beide Terme negativ, Reaktion läuft freiwillig ab |
ΔE negativ TΔS positiv Reaktion läuft nur bei niedrigen T freiwillig ab |
| Endoth. Reaktion: ΔE>0 |
ΔE positiv TΔS negativ Reaktion läuft nur bei hohen T freiwillig ab |
ΔE positiv TΔS positiv beide Terme positiv, Reaktion läuft nicht freiwillig ab |
Entropie und Prozesse
Da Entropie nicht vermindert werden kann, hat sie einen maßgeblichen Einfluss auf die Reversibilität von Prozessen. Generell unterscheidest du zwischen reversiblen und irreversiblen Prozessen.
- reversibler Prozess: die Entropie bleibt konstant
- irreversibler Prozess: die Entropie wird größer, da zum Beispiel durch Reibung Wärme entsteht
Somit kann die Entropie auch als Alternative zur Zeitmessung hergenommen werden. Mit zunehmender Entropie schreitet der irreversible Prozess weiter voran und ist nicht umkehrbar, da die Entropie nicht vernichtet werden kann. Sie kann lediglich auf ein anderes System übertragen werden.
Entropie bei reversiblen Prozessen
Ein reversibler Prozess ist ein Prozess, der sich derart umkehren lässt, dass der Ausgangszustand wieder erreicht werden kann, ohne dass dabei Änderungen in der Natur oder Umgebung zurückbleiben.
Das bedeutet, dass bei dem Prozess keine Entropie erzeugt wird.
Lässt du beispielsweise einen prall gefüllten Basketball fallen, dann ist der Zustand reversibel, wenn du die Reibung vernachlässigst.
Entropie bei irreversiblen Prozessen
Bei einem irreversiblen Prozess hingegen kann das System ohne zusätzliche Krafteinwirkung von außen nicht wieder in seinen Ausgangszustand zurückkehren.
Das wäre zum Beispiel der Fall, wenn wir die Reibung durch die Luft bei dem Fallenlassen des Basketballs mit berücksichtigen. Die Reibung erzeugt Wärme und damit erhöht sie die Entropie. Das ist zwar eine sehr kleine Wärmemenge, aber sie trägt trotzdem zur Irreversibilität des Prozesses bei.
Reale irreversible Prozesse führen zu einer Entropieproduktion im Inneren des Systems. Dann gilt:

Die sogenannte Entropieerzeugungsrate ist also immer positiv bei irreversiblen Prozesse.
Bei idealen reversiblen Prozessen ist die Entropieerzeugungsrate gleich null und folglich

Entropieänderung
Die Entropieänderung ΔS beschreibt die Entropie während eines reversiblen Prozesses.

 ist dabei die umgesetzte Wärmemenge und T die absolute Temperatur, bei der der reversible Prozess abläuft.
ist dabei die umgesetzte Wärmemenge und T die absolute Temperatur, bei der der reversible Prozess abläuft.
Wird nun die Wärme in einem System erhöht, so steigt auch die Entropie. Je höher die Temperatur bei der Wärmeerhöhung ist, desto weniger steigt die Entropie an.
Expertenwissen: Wahrscheinlichkeit eines Makrozustands
Die Wahrscheinlichkeit w eines Makrozustandes berechnest du folgendermaßen:
 ; mit
; mit 
- Der Index i beschreibt den jeweiligen Makrozustand.
- pi ist die Anzahl der Mikrozustände, die zu i gehören.
- p ist die Summe aller Mikrozustände über alle Makrozustände.
Wenn du die Formel nun auf unser Beispiel überträgst, musst du zunächst die Anzahl der Mikrozustände durch verschiedene Anordnungsmöglichkeiten bestimmen:
- Ein Atom: 5 Mikrozustände
- Zwei Atome: 10 Mikrozustände
- Drei Atome: 10 Mikrozustände
- Vier Atome: 5 Mikrozustände
- Fünf Atome: 1 Mikrozustand
Du kannst die Wahrscheinlichkeiten der Mikrozustände nun berechnen. Dabei siehst du, dass die Entropie der Makrozustände proportional zur Anzahl ihrer Mikrozustände ist.
Entropie – Definition — häufigste Fragen
(ausklappen)
Entropie – Definition — häufigste Fragen
(ausklappen)-
Was heißt Entropie als Zustandsgröße genau?Entropie ist eine Zustandsgröße, weil ihr Wert nur vom Zustand des Systems abhängt. Genau wie Druck oder Temperatur beschreibt sie ein System in der Thermodynamik, ohne den Weg dorthin zu berücksichtigen. Das Formelzeichen der Entropie ist S.
-
Warum wird Entropie oft als Unordnung erklärt?Entropie wird oft als Unordnung erklärt, weil mehr mögliche Teilchenanordnungen meist eine höhere Entropie bedeuten. Wenn Teilchen sich auf mehr Arten verteilen können, wirkt das „ungeordneter“. Zum Beispiel verteilt sich eine Parfümwolke mit der Zeit gleichmäßig in der Luft, wodurch die Entropie zunimmt.
-
Wie entscheidet die Anzahl der Mikrozustände über die Entropie?Je mehr Mikrozustände möglich sind, desto größer ist die Entropie. Mikrozustände sind verschiedene Anordnungen der Teilchen, die zum gleichen Makrozustand gehören. Wenn Teilchen sich auf viele Arten anordnen können, steigt die Anzahl der Mikrozustände und damit das Maß der Entropie.
-
Wie rechne ich eine Entropieänderung aus Wärme und Temperatur aus?Du berechnest die Entropieänderung bei einem reversiblen Prozess mit
 . Dabei ist
. Dabei ist  die reversibel zugeführte Wärmemenge und T die absolute Temperatur. Mehr zugeführte Wärme erhöht
die reversibel zugeführte Wärmemenge und T die absolute Temperatur. Mehr zugeführte Wärme erhöht  , höhere Temperatur verringert den Anstieg.
, höhere Temperatur verringert den Anstieg.
-
Wann läuft eine chemische Reaktion spontan ab über die Gibbs-Energie?Eine chemische Reaktion läuft spontan ab, wenn die Gibbs-Energie negativ ist, also
 . Du berechnest sie mit
. Du berechnest sie mit  . Ist
. Ist  , läuft die Reaktion nicht freiwillig ab; bei
, läuft die Reaktion nicht freiwillig ab; bei  schon.
schon.
Enthalpie
Du hast jetzt einiges über die Entropie gelernt. Eine weitere wichtige Zustandsgröße ist die Enthalpie. Schaue dir jetzt unser Video dazu an, um mehr über die Enthalpie zu erfahren!