Wärmeenergie
Wenn du schon einmal Wasser gekocht hast, dann bist du mit der Wärmeenergie in Kontakt gekommen. Das ist die Energie, die unter anderem dein Wasser zum Kochen bringt. In diesem Beitrag wollen wir die die Wärmeenergie näher bringen.
Du möchtest ganz entspannt lernen? Dann schaue dir jetzt unser Video zum Thema Wärmeenergie an! Hier bekommst du alles was du wissen musst in nur wenigen Minuten perfekt aufbereitet.
Inhaltsübersicht
Wärmeenergie einfach erklärt
Die Wärmeenergie (auch thermische Energie) ist ein Teil der inneren Energie eines Systems und beschreibt die Energie, die in der ungeordneten Bewegung der mikroskopischen Bestandteile des Systems (Atome, Moleküle) steckt.
In manchen Fällen wird die Wärmeenergie mit den Begriffen Wärme , Temperatur, innere Energie oder Wärmemenge gleichgesetzt. Der entsprechende Kontext, in dem der Begriff Wärmeenergie auftaucht, sollte mögliche Mehrdeutigkeiten vermeiden.
Wird die Erwärmung eines Körpers betrachtet, so findet man die Wärmeenergie (oder Wärmemenge) im Zusammenhang mit der Wärmekapazität des Körpers folgendermaßen vor
.
Hier steht 
für die Wärmeenergie in 
, 
für die Wärmekapazität in 
, 
für die Masse des Körpers und 
für die gewünschte Temperaturänderung in 
. Vereinzelnd findest du statt dem ein 
vor.
Wärmekapazität
Wenn du einem Körper Wärme zuführst, dann ändert sich seine Temperatur. Wie stark die Temperaturänderung ist, hängt von verschiedenen Faktoren ab. Du kannst dir leicht vorstellen, dass du mehr Energie benötigst, umso mehr Wasser du zum Beispiel erwärmen möchtest. Nehmen wir eine gleiche Menge an Wasser und Milch, dann benötigen wir zum Erreichen der gleichen Temperatur unterschiedlich viel Energie in Form von Wärme. Wir haben hier zum Vergleich Milch genommen, da diese eine andere Wärmekapazität als Wasser besitzt und wir daher nach der Formel im vorherigen Abschnitt eine andere Energiemenge erwarten. Diese zwei Beobachtungen können wir in folgender Formel festhalten
.
Du solltest bei dieser Formel aber darauf achten, welche Bedeutung die Wärmekapazität hat. Der Begriff Kapazität ist unglücklich gewählt worden, denn er könnte die falsche Vorstellung hervorrufen, dass es sich bei der Wärmeenergie um die Energie handelt, die der Körper aufnehmen kann. Tatsächlich ist aber nicht mehr als diejenige Energie, die notwendig ist, um die Temperatur eines bestimmten Körpers um den Betrag zu ändern.
Zusammenhang zur inneren Energie
Wie im ersten Abschnitt erwähnt wurde, ist die Wärmeenergie ein Teil der inneren Energie eines Systems. Der Zusammenhang zwischen innerer Energie 
und Wärmeenergie wird durch den 1. Hauptsatz der Thermodynamik
gegeben und lautet
.
Hier beschreibt 
die Änderung der inneren Energie eines Systems, wenn es von einem Zustand 1 in einen Zustand 2 übergeht. Dieser Übergang kann durch die Zu- oder Abfuhr von Wärmeenergie , durch die Verrichtung von Arbeit
oder beidem stattfinden.
Es ist wichtig, sich den Unterschied zwischen Wärme, Temperatur und innerer Energie bewusst zu machen. Wärme beschreibt einen Prozess, die Übertragung von Energie von einem System auf ein anderes aufgrund einer Temperaturdifferenz. Die Wärme ist also keine Zustandsgröße . Im Gegensatz dazu sind die Temperatur und die innere Energie Zustandsgrößen. Die Temperatur beschreibt die mittlere kinetische Energie der Atome oder Moleküle eines Systems. Die innere Energie gibt hingegen Auskunft über die Gesamtenergie eines Systems.
Ideales Gas
Im Fall des idealen Gases kann man tatsächlich die thermische Energie mit der Temperatur gleichsetzen. Für das ideale Gas gilt
.
Hier steht 
für die Boltzmann-Konstante
in 
, 
für die Temperatur in 
, 
für die Anzahl an Teilchen im Gas, 
für die Freiheitsgrade der Teilchen, 
für die Gaskonstante in 
und 
für die Stoffmenge in Mol
. Für weitere Details zu dieser Formel, kannst du dir gerne unseren Beitrag zur inneren Energie anschauen.
Wärmekapazität von Wasser
| Stoff | Wärmekapazität in  |
| Aluminium | 900 |
| Kupfer | 390 |
| Glas | 840 |
| Eisen | 450 |
| Silber | 230 |
| Holz | 1700 |
| Wasser (flüssig) | 4186 |
| Protein | 1700 |
Stell dir vor, du hast 20 kg Wasser und möchtest das von 
auf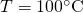 
erwärmen. Welche Wärmeenergie ist dafür notwendig? Damit wir diese Energie berechnen können, brauchen wir die spezifische Wärmekapazität des Wassers. Aus der obigen Tabelle entnehmen wir, dass Wasser im flüssigen Zustand eine Wärmekapazität von 
besitzt. Die Temperaturänderung ist in diesem Fall 
oder in Kelvin 
. Mit diesen Daten können wir die benötigte Wärmeenergie berechnen zu
.
Temperatur eines idealen Gases
Nehmen wir an, dass wir einen Mol eines idealen Gas haben und uns nur für die Translationsbewegungen der einzelnen Moleküle interessieren. Bei welcher Temperatur in Kelvin besitzt das Gas eine thermische Energie von 4150 
? Da wir es hier mit einem idealen Gas zu tun haben, können wir die Formel
verwenden. Wenn wir diese nach der Temperatur umstellen, erhalten wir
.
Setzen wir nun noch 
(da sich die Moleküle in drei Richtungen unabhängig bewegen können),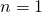 
und 
ein, so bekommen wir eine Temperatur von
.
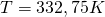