hx Diagramm
In diesem Artikel erklären wir dir, wie das hx-Diagramm aufgebaut ist. Es zeigt die Abhängigkeit der verschiedenen Zustandsgrößen bei konstantem Druck auf. Außerdem erläutern wir die Bedeutung der einzelnen Parameter und geben ein Beispiel zur Mischung zweier Luftmengen.
In unserem Video bauen wir das hx-Diagramm stückweise auf und zeigen dir gleich, wie das Diagramm aussieht. Außerdem erklären wir dir, wie man damit arbeitet.
Inhaltsübersicht
hx Diagramm Erklärung
Skala für Temperatur und absolute Feuchtigkeit
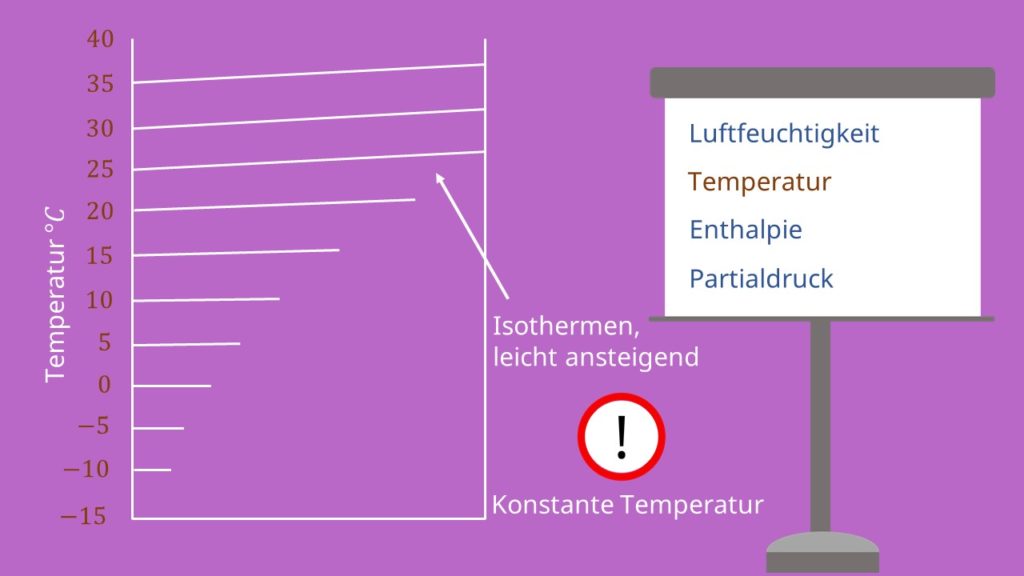
Zuerst zu den Hauptachsen des hx-Diagramms: Diese zeigen die Temperatur (y-Achse) und die absolute Feuchtigkeit (untere x-Achse) bei konstantem Umgebungsdruck. Die absolute Feuchtigkeit wird dabei in Gramm Wasser pro Kilogramm Luft gemessen, also der Einheit 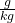 . Bezüglich der Temperatur gibt es zusätzlich auch noch Hilfslinien, die sogenannten Isothermen, die Zustände konstanter Temperatur im hx-Diagramm kennzeichnen. Sie verlaufen nur für 0°C parallel zur x-Achse wie unten im ersten Bild gezeigt. Für höhere Temperaturen steigen die Isothermen des hx-Diagramms zu höheren absoluten Feuchtigkeitswerten hin an. Diese Darstellung ermöglicht es später, leichter die Enthalpieveränderungen direkt aus dem Diagramm abzulesen.
. Bezüglich der Temperatur gibt es zusätzlich auch noch Hilfslinien, die sogenannten Isothermen, die Zustände konstanter Temperatur im hx-Diagramm kennzeichnen. Sie verlaufen nur für 0°C parallel zur x-Achse wie unten im ersten Bild gezeigt. Für höhere Temperaturen steigen die Isothermen des hx-Diagramms zu höheren absoluten Feuchtigkeitswerten hin an. Diese Darstellung ermöglicht es später, leichter die Enthalpieveränderungen direkt aus dem Diagramm abzulesen.
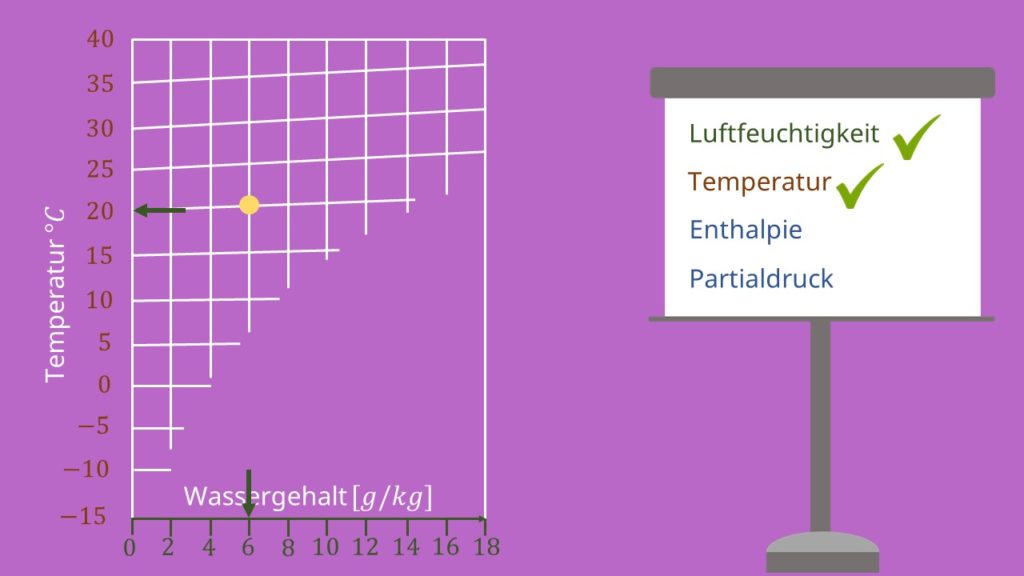
Senkrecht zu den Isothermen sieht man weitere Hilfslinien. Sie zeigen die Zustände an, bei denen die absolute Feuchtigkeit konstant bleibt, also die Luft nicht weiter be- oder entfeuchtet wird. Fügt man diese Hilfslinien zu den bereits vorhandenen Isothermen hinzu, ergibt sich der folgende, unten sichtbare Teil des hx-Diagramms. So hat der eingezeichnete Punkt im unteren hx-Diagramm beispielsweise den Temperaturwert 20°C und eine absolute Feuchtigkeit von 6g/kg.
Partialdruck
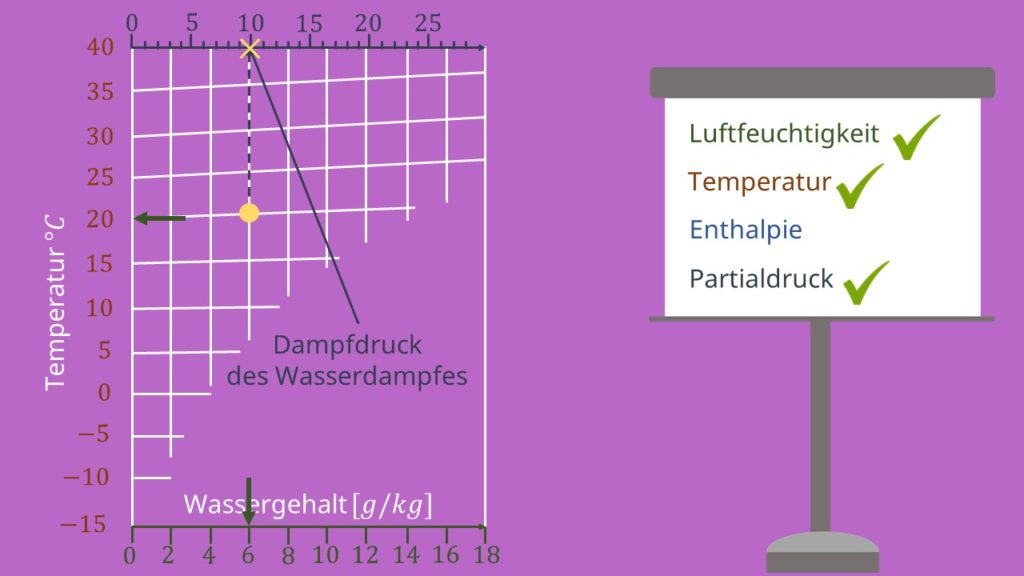
Zusätzlich zu den bereits erwähnten Größen wird noch eine weitere x-Achse oben im hx-Diagramm angezeigt, die den sogenannten Partialdruck des gesiedeten Wassers angibt. Der Partialdruck beschreibt hier den Druck, der zusätzlich zur Luft entsteht, wenn Wasser in die Gasphase wechselt. Da der Partialdruck des Wassers in der Luft proportional zum Wassergehalt in der Luft ist, lässt er sich durch Ziehen einer vertikalen Linie vom eingezeichneten Punkt aus hin zur oberen x-Achse bestimmen. Diese Linie ist immer parallel zu den Hilfslinien, die die konstante, absolute Feuchtigkeit anzeigen. Ein Beispiel ist unten im nächsten Bild zu sehen. Ausgehend von einem Wert der absoluten Feuchtigkeit von x= 6g/kg erhält man durch Entlanglaufen einer der Hilfslinien des hx-Diagramms nach oben den Wert des Partialdrucks von 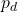 = 9,5mbar
= 9,5mbar
Sättigungslinie
Weiterhin kann die Luft bei einer gegebenen Temperatur immer nur so viel Wasser aufnehmen bis der Gesamtdruck aus den Partialdrücken von gesiedetem Wasser und der trockenen Luft dem Dampfdruck des Wassers bei dieser Temperatur entspricht, denn dann ist für das Wasser ein Kräfte-Gleichgewicht zwischen Flüssig- und Gasphase erreicht.
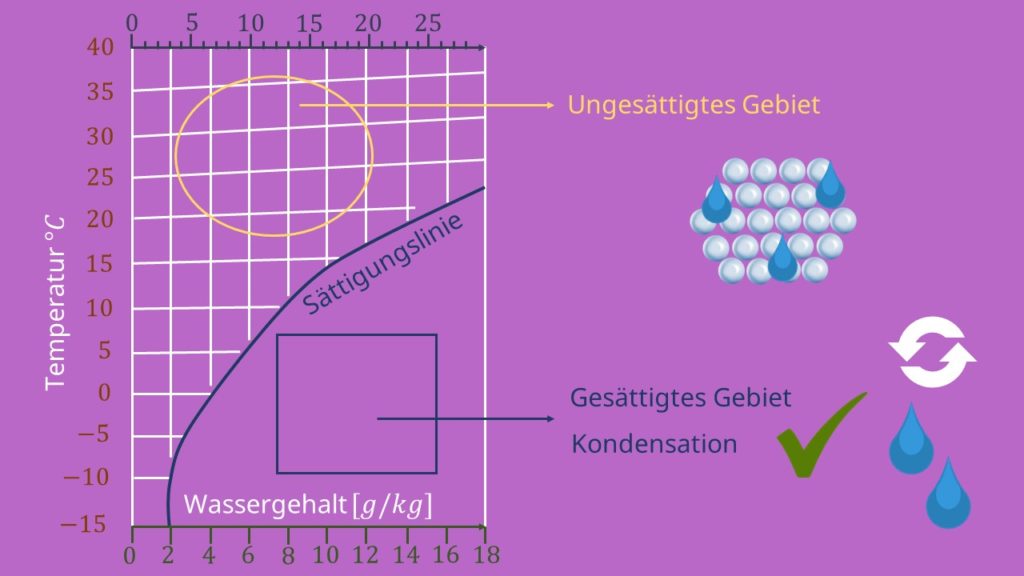
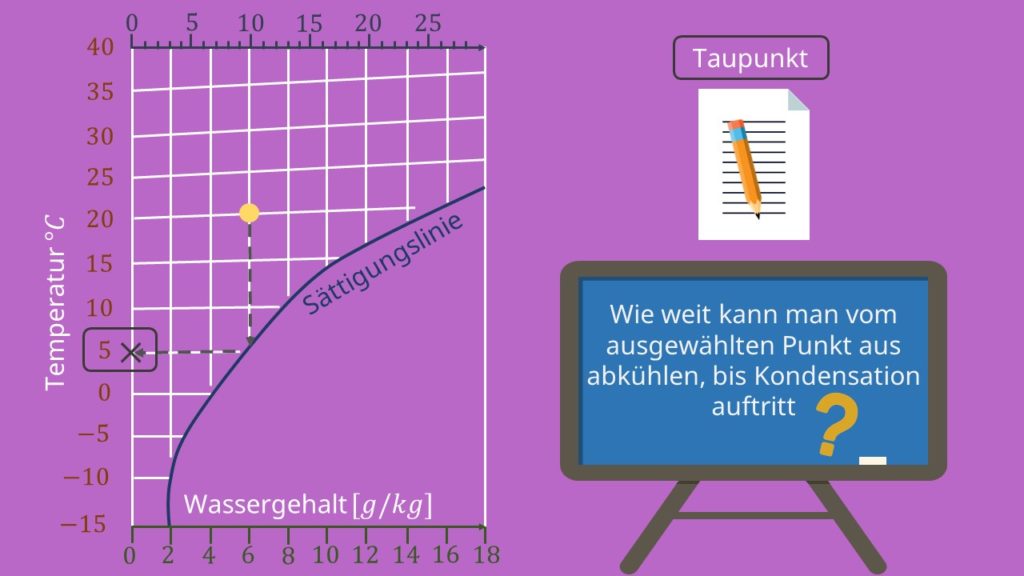
Versucht man die Luftfeuchtigkeit über diesen Punkt zu erhöhen, geht man also im Diagramm entlang einer der horizontalen Hilfslinien, kommt es zur Kondensation des Wassers aus der Luft. Dieser Zustand wird im hx-Diagramm durch die sogenannte Sättigungslinie (unten rechts im nächsten Bild) dargestellt, wobei alles über der Sättigungslinie ungesättigte Luft ist und alles unter dieser Linie übersättigte Luft ist und somit dann Kondensation aus der Luft stattfindet. Die Sättigungslinie selbst entspricht also immer dem Zustand mit dem maximalem Feuchtigkeitsgehalt bei gegebener Temperatur. Da die maximal mögliche Sättigung der Luft an Wasser mit zunehmender Temperatur zunimmt, steigt die Sättigungslinie im hx-Diagramm zu höheren Temperaturen hin an. So kann also eine Kondensation aus der Luft umgekehrterweise auch durch eine Abkühlung (man läuft im Diagramm entlang einer der vertikalen Linien nach unten bis zur Sättigungslinie) bei gleichbleibendem absoluten Feuchtigkeitsgehalt bewirkt werden.
Taupunkt und Sättigungsdruck
Weitere wichtige Werte, die einen Zustand im hx-Diagramm charakterisieren, sind der Taupunkt und der Sättigungsdruck. Geht man von einem beliebigen Zustand aus nach rechts parallel zu einer der Isothermen, schneidet man irgendwann die Sättigungslinie, ab der dann Kondensation eintritt. Die Temperatur an diesem Schnittpunkt beschreibt dann den Taupunkt. Der Sättigungsdruck dagegen ist der Partialdruck des Wassers in der Luft, der herrscht, wenn die Kondensation bei einer gegebenen Temperatur eintritt. Man bestimmt ihn, indem man, wie zuvor, parallel zu einer der Isothermen nach rechts läuft bis man die Sättigungslinie schneidet. Von diesem Schnittpunkt aus folgt man anschließend einer geraden Linie nach oben, wie im unteren Bild gezeigt, die dann die Partialdruckskala schneidet. Dieser erhaltene Schnittpunkt gibt dann den Sättigungsdruck an.
Relative Feuchtigkeit φ
Zusätzlich zur absoluten Feuchte kann die Feuchtigkeit auch noch relativ im hx-Diagramm erfasst werden. Diese sogenannte relative Feuchtigkeit φ entspricht dem Bruchteil, den die aktuelle Feuchtigkeit an der maximal möglichen Feuchtigkeit bei gegebener Temperatur ausmacht. Somit entspricht die relative Feuchtigkeit entlang der Sättigungslinie immer 100%. Zusätzlich sind in dem Diagramm meistens Kurven angegeben, entlang derer die relative Feuchtigkeit konstant Werte wie 50% bzw. 75% beträgt. Die relativen Feuchtigkeitswerte werden grundsätzlich am Ende der Kurve angegeben.
Enthalpie im hx-Diagramm
Eine weitere wichtige Zustandsgröße im hx-Diagramm ist die Enthalpie. Sie ist eine thermodynamische Zustandsgröße und ist folgendermaßen definiert:
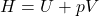
U = „innere Energie“ , p = „Druck“ , V = „Volumen“
Die Enthalpie ist immer davon abhängig, was man als zugehöriges System definiert. Hier ist die Enthalpie sowohl auf die Luft als auch auf den Wasserdampf in der Luft selbst bezogen. Deswegen wird bei der Enthalpie im Diagramm auch oft der Index (1+x) hinzugefügt, wobei die 1 sich auf die Enthalpie der trockenen Luft und x auf die Enthalpie des Wassers in der Luft bezieht. Die angegebene Enthalpie ist dabei normiert auf das Gewicht der trockenen Luft ohne das zugehörige Gewicht des Wassers. Dass beide Enthalpiebeiträge der Luft und des Wassers berücksichtigt werden, ist insofern wichtig, da die Wärmekapazität von Wasser deutlich höher ist als die von trockener Luft und somit das verdampfte Wasser ebenfalls einen großen Anteil an Wärme speichert und damit auch einen großen Anteil an der Enthalpie des Gesamtgemisches hat.
Isenthalpe h(1+x)-Kurven
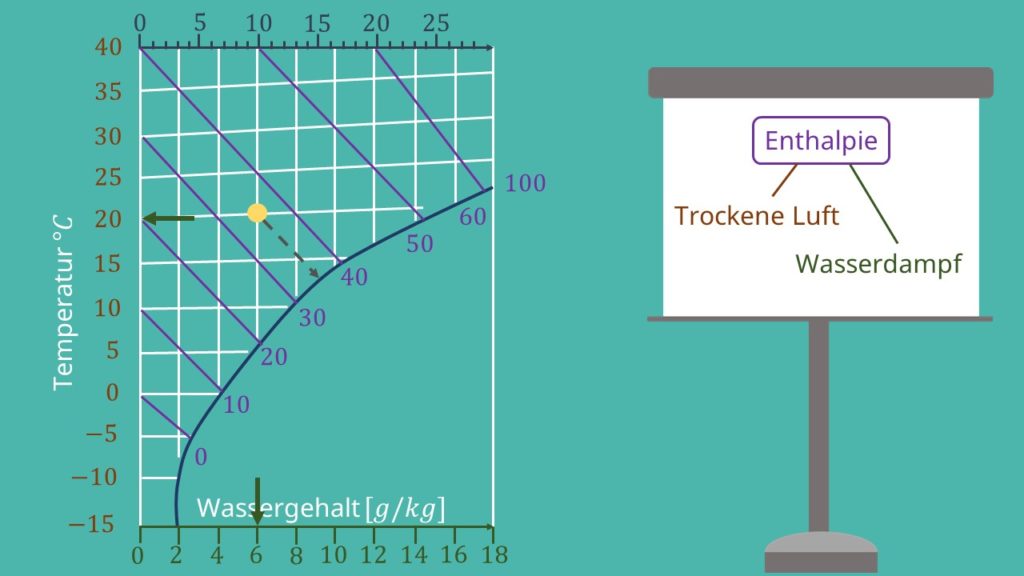
Um das Ablesen von Enthalpieveränderungen im hx-Diagramm zu ermöglichen, sind isenthalpe Kurven eingezeichnet, entlang derer die Enthalpie konstant bleibt. Die an diesen Kurven angegebenen Enthalpiewerte geben dabei immer die Differenz zum Wert bei 0ºC und 0g/kg Feuchtigkeitsgehalt an, der als Nullpunkt gewählt wurde. Dort entspricht die Enthalpie also 0 kJ/kg. Von diesem Punkt ausgehend kann dann die Enthalpie für jede Zusammensetzung und Temperatur berechnet werden, indem man die Leistungsbeiträge für die jeweilige Erwärmung von Wasser und Luft einfach addiert, da die Enthalpie eine Zustandsfunktion ist.
Die Phasenübergänge von Wasser von den Zuständen flüssig zu gasförmig und umgekehrt müssen nicht berücksichtigt werden, da diese isenthalp ablaufen. Hierbei kommt es nur zu einer Umwandlung von innerer Energie (U) der Luft zu Druck-Volumen Arbeit (pV-Anteil der Enthalpie), die das Wasser beim Phasenübergang verrichtet. Beide Beiträge sind aber Teil der Enthalpie und weisen unterschiedliche Vorzeichen auf und heben sich so auf. Es kommt lediglich zur Verschiebung von Energie, zuvor in der Luft als sensible Wärme gespeichert und nun als latente Wärme im verdampften Wasser gespeichert. Diese Verschiebung macht sich als Abkühlung der Luft bemerkbar. Dieser steigende Anteil an latenter Wärme ist in dem hx-Diagramm als leicht ansteigende Isothermen berücksichtigt.
Durch diese ansteigenden Isothermen lassen sich die isenthalpen Kurven parallel zueinander darstellen, was das Ablesen von Enthalpieänderungen beim Übergang zwischen zwei Zuständen stark vereinfacht. Die isenthalpen Kurven verlaufen im hx-Diagramm schräg von links oben nach rechts unten, wie im folgenden Bild dargestellt. Für die Berechnung der Enthalpieänderung muss man die Differenz zwischen den beiden Enthalpiewerten bilden, die am Ende der isenthalpen Kurven angegeben sind.
Dichte ρ
Zuletzt gibt es noch eine weitere wichtige Größe, die aus dem hx-Diagramm erfasst werden kann: die Dichte ρ. Dabei gilt, dass mit steigender Temperatur sich das Luft-Wasser Gemisch ausdehnt und somit sich die Dichte verringert. Außerdem ist der Wasserdampf leichter als die Luft, somit sinkt mit steigendem Feuchtigkeitsgehalt der Luft die Dichte. Beim Ablesen der Dichte aus diesem hx-Diagramm sollte man immer beachten, dass der Druck für den es konstruiert worden auch dem eigenen vorhandenen Druck entspricht, da die Dichte und die anderen Zustandsgrößen auch vom gewählten Druck abhängen.
Bereiche konstanter Dichte können anhand der gestrichelten, leicht geneigten Linien im hx-Diagramm abgelesen werden. Zur Ermittlung der Dichte eines Zustands muss man vom gegebenen Zustand dieser Linie im hx-Diagramm zur y-Achse folgen, wo neben den Temperaturwerten auch die Dichtewerte angegeben sein können. Der Schnittpunkt zwischen den beiden Linien gibt dann die Dichte an.
Luftbefeuchtung
Trockene Luft kann durch Kontakt mit Wasser oder Zuführen von Wasserdampf befeuchtet werden. Dadurch ändert sich der sowohl die absolute Feuchtigkeit 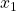 um den Betrag Δx, sondern auch die Enthalpie
um den Betrag Δx, sondern auch die Enthalpie 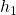 um den Betrag Δh. Die neuen Zustände der befeuchteten Luft ergeben sich dann einfach durch die Addition der Änderungen und der ursprünglichen Zustandswerte:
um den Betrag Δh. Die neuen Zustände der befeuchteten Luft ergeben sich dann einfach durch die Addition der Änderungen und der ursprünglichen Zustandswerte:
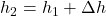
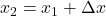
Beispiel: Mischen zweier Luftmengen
Mischt man zwei konstante Luftströme 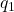 und
und 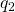 mit der Einheit [kg/h], die beide jeweils unterschiedliche Zustände
mit der Einheit [kg/h], die beide jeweils unterschiedliche Zustände 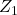 und
und 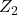 im hx-Diagramm aufweisen, dann lässt sich über eine grafische Methode der neue Zustand
im hx-Diagramm aufweisen, dann lässt sich über eine grafische Methode der neue Zustand 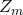 des Gemisches herausfinden. Dafür zeichnet man beide Zustände
des Gemisches herausfinden. Dafür zeichnet man beide Zustände 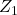 und
und 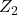 in das HX-Diagramm ein und verbindet beide über eine Gerade. Der Mischzustand
in das HX-Diagramm ein und verbindet beide über eine Gerade. Der Mischzustand 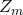 befindet sich auf dieser Gerade, wobei er näher an dem Zustand liegt, der den größeren Anteil am Gesamtluftstrom hat. Weiterhin lassen sich Längen
befindet sich auf dieser Gerade, wobei er näher an dem Zustand liegt, der den größeren Anteil am Gesamtluftstrom hat. Weiterhin lassen sich Längen 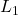 und
und 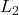 ablesen, die den jeweiligen Abstand zwischen den Zuständen
ablesen, die den jeweiligen Abstand zwischen den Zuständen 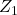 und
und 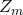 , bzw.
, bzw. 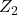 und
und 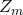 bezeichnen. Diese sind beispielhaft in der unteren Darstellung eingezeichnet. Zwischen den Luftströmen und den Längenabständen existiert eine umgekehrte Proportionalität, die sich folgendermaßen ausdrücken lässt:
bezeichnen. Diese sind beispielhaft in der unteren Darstellung eingezeichnet. Zwischen den Luftströmen und den Längenabständen existiert eine umgekehrte Proportionalität, die sich folgendermaßen ausdrücken lässt:
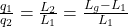
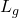 = Gesamtlänge der Gerade
= Gesamtlänge der Gerade
Durch Umstellen ergibt sich dann:
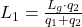
Nimmt man beispielhaft an, dass in einer Lüftungsanlage ein Außenluftstrom 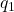 = 1500kg/h mit dem Zustand
= 1500kg/h mit dem Zustand 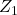 ( θ=5ºC und φ=50% r.F.) gemischt wird mit einem Umluftstrom
( θ=5ºC und φ=50% r.F.) gemischt wird mit einem Umluftstrom 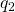 =2500kg/h mit dem Zustand
=2500kg/h mit dem Zustand 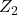 ( θ=20°C und φ=60% r.F.), so zeichnet man die beiden Punkte zuerst in das hx-Diagramm ein, wie im unteren Bild. Anschließend verbindet man beide mit einer Geraden und misst die Gesamtlänge der gezeichneten Geraden aus, in diesem Fall 64mm.
( θ=20°C und φ=60% r.F.), so zeichnet man die beiden Punkte zuerst in das hx-Diagramm ein, wie im unteren Bild. Anschließend verbindet man beide mit einer Geraden und misst die Gesamtlänge der gezeichneten Geraden aus, in diesem Fall 64mm.
Nun muss man die Werte nur noch in oben genannte Formel einsetzen, um 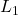 zu ermitteln :
zu ermitteln :
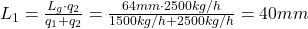
Abschließend misst man vom Zustand 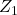 die 40mm entlang der Geraden ab und erhält so den Mischpunkt
die 40mm entlang der Geraden ab und erhält so den Mischpunkt 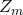 . Dieser hat dann folgende Werte: θ=14,4°C,
. Dieser hat dann folgende Werte: θ=14,4°C, 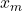 =6,5g/kg,
=6,5g/kg, 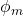 =64% r. F. .
=64% r. F. .