Isentroper und polytroper Wirkungsgrad
Was sind Isentrope und polytrope Wirkungsgrade eigentlich? Das erklären wir dir in diesem Beitrag.
Inhaltsübersicht
Wirkungsgrade bestimmen
Du bist sicher schon mal mit einem Flugzeug geflogen. Die Triebwerke arbeiten mit Verdichtern und Turbinen. Wie du mit dem polytropen und dem isentropen Wirkungsgrad deren Effizienz bestimmen kannst, erfährst du jetzt.
Der Wirkungsgrad allgemein ist das Verhältnis der Leistung des realen Prozesses und des idealen Prozesses. Der ideale Prozess ist der Prozess, wenn wir keine Verluste hätten. In Turbinen und Verdichtern entstehen die Verluste durch Reibungseffekte mit der Wand, aber auch innerhalb des Fluids selbst.
Isentroper Wirkungsgrad
Wir beginnen mit dem isentropen Wirkungsgrad.
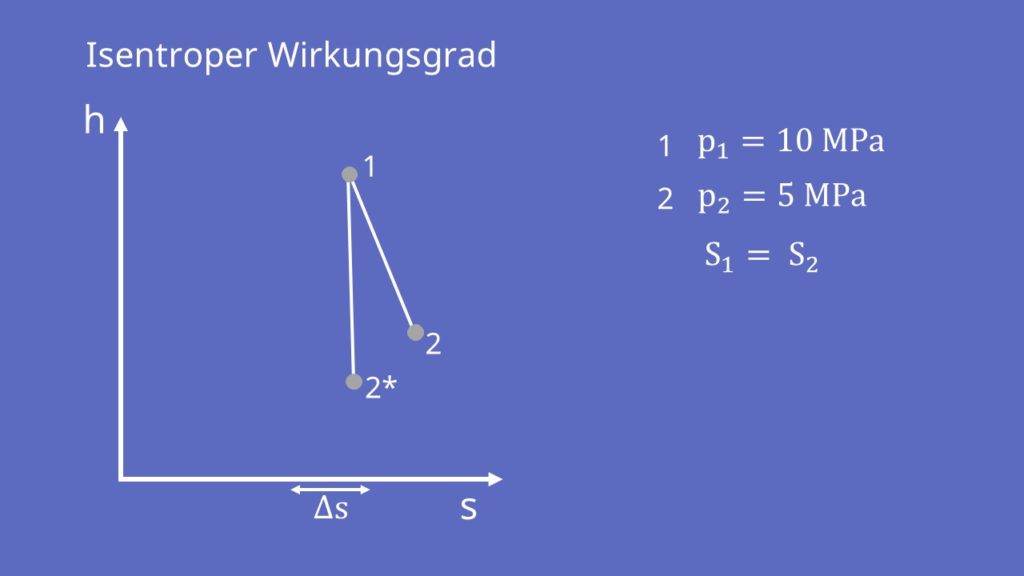
Du erkennst sicher am Namen, dass wir hier einen Vergleich zum isentropen Prozess ziehen, bei dem die Entropieänderung gleich Null ist. Um dir das graphisch zu zeigen, gehen wir in das h-s-Diagramm.
Betrachten wir die Änderung von Zustand eins bei einem Druck von 10 Megapascal. Wir laufen jetzt durch eine Turbine und entspannen auf 5 Megapascal. Dabei steigt gemäß dem zweiten Hauptsatz natürlich die Entropie. Im idealen Fall würde die Entropie jedoch konstant bleiben. Somit wäre die spezifische Arbeit, die wir erhalten würden, größer als im realen Fall. Dieser Zustand wird als „zwei Stern“ bezeichnet.
Also ermitteln wir für die Turbine einen isentropen Wirkungsgrad von:
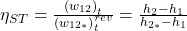
Für den Verdichter können wir analog vorgehen, wir beginnen wieder bei Punkt eins. Allerdings muss man hier im realen Fall mehr Arbeit reinstecken, um Verluste zu kompensieren. Der isentrope Fall hat somit eine geringere Enthalpie und der Bruch dreht sich entsprechend um zu:
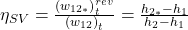
Stellen wir uns vor wir verdichten von Zustand eins mit der spezifischen Enthalpie von 10 Kilojoule pro Kilogramm auf die Enthalpie h zwei von 20 kilojoule pro kilogramm. Für den idealen Prozess ergäbe sich die Enthalpie:
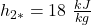
Setzen wir die Zahlenwerte ein, ergibt sich also ein Wirkungsgrad von 80 Prozent.
Als nächstes rufen wir uns nochmal die reversible spezifische Entropiebilanz für den stationären Fließprozess ins Gedächtnis:
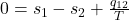
In unserem Fall ist die Entropie im Zustand eins gleich der Entropie in Zustand zwei. Wir erhalten, dass der Wärmestrom auch Null sein muss und die Turbine beziehungsweise der Verdichter adiabat sind. Du kannst dir sicher vorstellen, dass das in der Realität nicht so einfach möglich ist.
Polytroper Wirkungsgrad
Dementsprechend brauchen wir noch den polytropen Wirkungsgrad. Wir verwenden hier die allgemeine Definition der technischen Arbeit, da diese keine Einschränkungen bezüglich der Entropie macht:
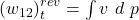
Damit erhalten wir für Turbine und Verdichter:
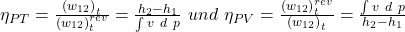
Der Unterschied ist also, dass der polytrope Wirkungsgrad keine isentrope Zustandsänderung voraussetzt. Das heißt die reversible Expansion, beziehungsweise Verdichtung, muss nicht isentrop geschehen.
Damit kannst du nun also auch die Effizienz eines Triebwerks bestimmen. Viel Erfolg und bis bald!