Wärmedurchlasswiderstand
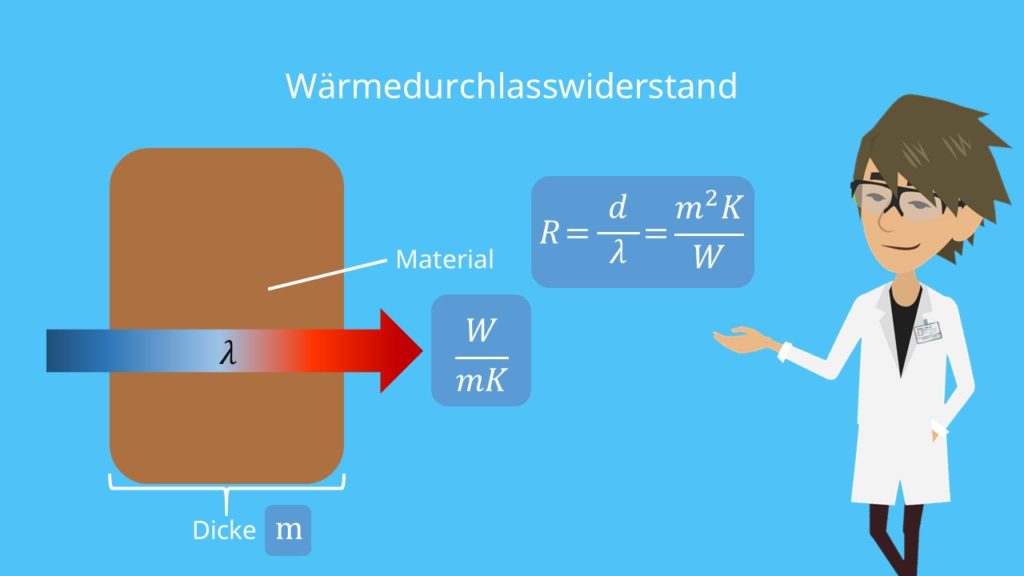
Der Wärmedurchlasswiderstand ist der Widerstand, den ein homogenes Bauteil selbst bei der Übertragung von Wärme dem Wärmestrom entgegenbringt. Dieser Widerstand ist abhängig von der Dicke des Bauteils, aber auch von dem verwendeten Material.
Inhaltsübersicht
Wärmedurchlasswiderstand Formel
Der Wärmedurchlasswiderstand wird mit der folgenden Formel berechnet:

Dabei steht d für die Dicke des Bauteils in Metern und  beschreibt die Wärmeleitfähigkeit des verwendeten Baustoffes in
beschreibt die Wärmeleitfähigkeit des verwendeten Baustoffes in  . Der Wärmedurchlasswiderstand hat somit die Einheit
. Der Wärmedurchlasswiderstand hat somit die Einheit  .
.
Mineralwolle zum Beispiel, hat eine geringere Wärmeleitfähigkeit als Metall. Dadurch ergibt sich für Mineralwolle ein höherer Wärmedurchlasswiderstand und eine bessere Dämmeigenschaft.
Die Wärmeleitfähigkeit  kann für verschiedene Baustoffe in entsprechenden Tabellen eingesehen werden und ist ein feststehender Wert. Ausschlaggebend hierfür ist die DIN 4108 zum Wärmeschutz.
kann für verschiedene Baustoffe in entsprechenden Tabellen eingesehen werden und ist ein feststehender Wert. Ausschlaggebend hierfür ist die DIN 4108 zum Wärmeschutz.
Wärmedurchlasswiderstand Berechnung
Um den Wärmedurchlasswiderstand zu berechnen, müssen die Werte für die Dicke des Bauteils sowie seine Wärmeleitfähigkeit in die Formel eingesetzt werden. Bei einem Bauteil mit beispielsweise zwei Schichten aus unterschiedlichen Materialien, können die Widerstände hierfür einfach zu einem Gesamtwiderstand addiert werden.
Die Formel ist beliebig erweiterbar, je nachdem wie viele Schichten betrachtet werden. Dies sieht wie folgt aus:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispielrechnung Wärmedurchlasswiderstand
Zum besseren Verständnis wollen wir uns das Ganze an einem Beispiel anschauen. Dafür berechnen wir den Wärmedurchlasswiderstand für eine 15 Zentimeter dicke Betonplatte, die von einer 10 Zentimeter dicken Dämmung aus Mineralwolle geschützt wird.
Betrachtet werden also zwei Schichten. Für die Berechnung müssen noch die Wärmeleitfähigkeiten der untersuchten Materialien herangezogen werden. Für Beton ergibt sich ein Lambda-Wert von 2,1 und für Mineralwolle 0,04  .
.
Mit der Formel von vorhin  kann die Ausgangsgleichung für den Wärmedurchlasswiderstand des gesamten Bauteils aufgestellt werden.
kann die Ausgangsgleichung für den Wärmedurchlasswiderstand des gesamten Bauteils aufgestellt werden.


Durch Einsetzen der gegebenen Werte in die Formel erhält man:

Für den Wärmedurchlasswiderstand der Betonplatte ergibt sich 0,0714  und für die Mineralwolle 2,5
und für die Mineralwolle 2,5  .
.

Der gesamte Widerstand für die 15 Zentimeter Betonplatte inkl. der 10 Zentimeter Dämmung beträgt also 2,5714  .
.
Wärmedurchlasskoeffizient
Der Wärmedurchlasskoeffizient Λ ist der Kehrwert des Wärmedurchlasswiderstands und ist dementsprechend durch folgende Formel definiert:

Er gibt die Wärmeleistung in Watt an, welche durch 1  eines Stoffes mit der Dicke d und bei einem Temperaturunterschied von 1 Kelvin an beiden Oberflächen hindurchgeht. Die Einheit von
eines Stoffes mit der Dicke d und bei einem Temperaturunterschied von 1 Kelvin an beiden Oberflächen hindurchgeht. Die Einheit von  wird in
wird in  angegeben.
angegeben.
Anhand des vorherigen Beispiels der Betonplatte und ihrer Dämmung kann ebenfalls der Wärmedurchlasskoeffizient berechnet werden. Auch hier gilt: der Wärmedurchlasskoeffizient des gesamten Bauteils ist gleich der Einzelkoeffizient der Betonplatte plus dem der Mineralwolle.

Anschließend werden die entsprechenden Werte in die Formel eingesetzt:


Dadurch erhalten wir die Wärmekoeffizienten von Beton und Mineralwolle als Teillösung mit 14 und 0,4  .
.
Der Wärmedurchlasskoeffizient für das gesamte Bauteil mit seinen zwei Schichten beträgt dann 14,4  .
.

Wie bereits erwähnt ist der zugehörige Koeffizient immer der Kehrwert des Widerstandes. Das kann einfach gegengeprüft werden. Aber Achtung! Hier darf nicht einfach der Kehrwert des oben berechneten Ergebnisses für das gesamte Bauteil verwendet werden! Stattdessen müssen zuerst die Kehrwerte der einzelnen Widerstände ausgerechnet und diese dann aufsummiert werden.
Wärmedurchlasskoeffizient 
Also ergibt sich für den Wärmedurchlasskoeffizient:
Wärmedurchlasskoeffizient 
Die kleine Abweichung in der zweiten Nachkommastelle ist der Rundung der einzelnen Teilergebnisse geschuldet.