Video anzeigen

Erzwungene Konvektion – längsumströmte, ebene Platte

Wichtige Inhalte in diesem Video

Turbulente und Laminare Strömungen und ihre Berechnung

Erzwungene Konvektion – Nusselt-Zahl und Korrekturfaktor

In diesem Beitrag erklären wir dir allen Wichtige zur erzwungenen Konvektion bei längsumströmten, ebenen Platten.

Inhaltsübersicht

Turbulente und Laminare Strömungen und ihre Berechnung

im Videozur Stelle im Video springen

Was die erzwungene Konvektion mit einer Heizung zu tun hat, weißt du bereits und auch mit den Begriffen laminare Strömung und turbulente Strömung kannst du etwas anfangen. Du weißt aber sicherlich auch, dass ein fahrendes Auto einen Luftwiderstand erfährt und deshalb auch von Luft umströmt wird. Wenn der Luftstrom warm ist, kann an der Oberfläche des Autos erzwungene Konvektion stattfinden, also ein Wärmeübergang von der warmen Luft auf deine kühlere Autooberfläche.

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Konvektion – beispielhafte Darstellung

Und genau das ist der Grund, wieso sich dein Auto erwärmt. Da das Auto angetrieben wird, fällt der Wärmeübergang hier in den Bereich der erzwungenen Konvektion. Um die erzwungene Konvektion berechnen zu können, betrachten wir die Kontur des Autos vereinfacht als eine ebene Platte.

Wir brauchen auch hier wieder die dimensionslosen Kennzahlen, um am Ende über die Nusselt-Zahl zum Wärmeübergang zu kommen.

Laminare und turbulente Strömung

Zuerst einmal musst du wieder die Reynoldszahl berechnen, um deine Strömungsart herauszufinden. Dabei ist dieses Mal ${\rm Re}_{krit}=\ 5\ast10^5$ . Ist dein berechneter Wert $Re\le5\ast10^5$ , handelt es sich um eine laminare Strömung. Wenn $Re>5\ast10^5$ ist, dann haben wir eine turbulente Strömung vorliegen. Auch hier gibt es eine Art Übergangsbereich. Wenn die Platte so gestaltet ist, dass die Vorderkante günstig gestaltet ist, also nicht stumpf ist, dann haben wir eine turbulente Grenzschicht mit laminarem Anlauf. Das bedeutet, dass wir am Anfang eine laminare Strömung haben, die dann zu einer turbulenten Strömung wird. Dabei gilt 10<Re<10^7 . Die Reynoldszahl berechnest du mit:

$Re=\frac{\omega\ast L}{\nu}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Laminare Strömung und turbulente Strömung – Reynoldszahl berechnen

Dabei ist $\nu$ wieder die kinematische Viskosität. ist hier die Plattenlänge und $\omega$ die Anströmgeschwindigkeit, also in unserem Beispiel die Geschwindigkeit, mit dem das Auto fährt, vorausgesetzt es geht kein Wind.

Wenn du deine Strömungsart bestimmt hast, kannst du die Nusselt-Zahl ausrechnen. Die Formel für die laminare Strömung lautet:

${\rm Nu}_{lam}=0,664\ast\sqrt{Re}\ast\sqrt[3]{Pr}$

Bei turbulenter Strömung berechnest du deine Nusselt-Zahl mit:

${\rm Nu}_{tur}=\frac{0,037\ast{Re}^{0,8}\ast Pr}{1+2,443\ast{Re}^{-0,1}\ast({Pr}^\frac{2}{3}-1)}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Strömungsart bestimmen und Nusselt-Zahl berechnen

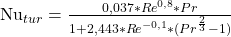
Um den Nu-Wert mit laminarem Anlauf bestimmen zu können, brauchst du wieder sowohl die Nusselt-Zahl aus der laminaren Strömung als auch die aus der turbulenten Strömung. Du rechnest also mit:

$Nu=\sqrt{{{\rm Nu}_{lam}}^2+{{\rm Nu}_{turb}}^2}$

Erzwungene Konvektion – Nusselt-Zahl und Korrekturfaktor

im Videozur Stelle im Video springen

Du wirst dir bestimmt denken können, dass wir auch hier die Nusselt-Zahl wieder korrigieren müssen. Dazu brauchst du den Korrekturfaktor K_T , der den Richtungseinfluss des Wärmestroms mitberücksichtigt. Für Flüssigkeiten berechnest du den Korrekturfaktor mit:

$K_{t},_{l}}\ =\ (\frac{Pr}{Pr_w})^{0,25}$

und für Gase mit:

$K_{T},_{g}=\ (\frac{T_{bez}}{T_w})^{0,12}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Korrekturfaktor berechnen

Zur Erinnerung: $\Pr_W$ ist die Prandtl-Zahl bei Wandtemperatur T_W und „nur Pr“ die Prandtl-Zahl bei Bezugstemperatur. Da dieses Mal der Körper umströmt wird, berechnest du die Bezugstemperatur mit:

${T}_{bez}=\frac{T_w+T_\infty}{2}$

Mit deiner korrigierten Nusselt-Zahl ${\rm Nu}_K=Nu\ast K_T$ kannst du dann deinen Wärmeübergangskoeffizienten bestimmen. Da auch in diesem Modell $Nu\ =\frac{\alpha\ast L}{\lambda}$ gilt, lautet die umgestellte Formel:

$\alpha=\frac{Nu\ast\lambda}{L}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Wärmeübergangskoeffizient berechnen

So, jetzt haben wir es geschafft. Nun kennst du dich bei der erzwungenen Konvektion bestens aus und weißt, was die laminare Strömung und die turbulente Strömung sind.

Beliebte Inhalte aus dem Bereich Wärmelehre

Konvektiver Wärmeübergang

Erzwungene Konvektion - Durchströmte Rohrleitung

Erzwungene Konvektion - längsumströmte, ebene Platte

Erzwungene Konvektion - Querumströmter Körper

Natürliche Konvektion

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .