Was versteht man unter Wärmeübergang?

Wärmeübergang ist die Übertragung von Wärmeenergie über eine Grenzfläche zwischen zwei Systemen oder Stoffen mit unterschiedlicher Temperatur. An der Grenzfläche fließt Wärme vom höheren zum niedrigeren Temperaturniveau, bis sich die Temperaturen annähern. Der Wärmeübergang kann je nach Situation durch Leitung, Konvektion oder Strahlung geprägt sein.

Wie berechnet man den Wärmeübergangskoeffizienten?

Den Wärmeübergangskoeffizienten berechnet man aus einer passenden Wärmeübergangs-Beziehung, zum Beispiel aus durch Umstellen zu . Konkret: , , , ergibt .

Was ist der Unterschied zwischen lokalem und mittlerem Wärmeübergangskoeffizienten?

Der lokale Wärmeübergangskoeffizient beschreibt den Wärmeübergang an einem bestimmten Ort der Oberfläche und kann sich entlang der Fläche ändern. Der mittlere Wärmeübergangskoeffizient fasst den Wärmeübergang über eine ganze Fläche oder eine charakteristische Länge zu einem einzigen Ersatzwert zusammen. Deshalb nutzt man lokal eher für detaillierte Profile und mittel eher für technische Überschlagsrechnungen.

Warum bedeutet ein hoher Wärmeübergangskoeffizient eine schlechtere Wärmedämmung?

Ein hoher Wärmeübergangskoeffizient bedeutet eine schlechtere Wärmedämmung, weil bei gleichem Temperaturunterschied mehr Wärme pro Fläche und Zeit durch die Stoffgrenze übertragen wird. Mathematisch ist der zugehörige Wärmeübergangswiderstand der Kehrwert, also . Ein größeres entspricht deshalb einem kleineren Widerstand.

Video

Hier geht's zum Video „Wärmeübergangswiderstand“

Hier geht's zum Video „Konvektiver Wärmeübergang“

Wärmeübergangskoeffizient

Name: Wärmeübergangskoeffizient
Uploaded: 2026-06-23T17:40:18Z
Duration: 4 min 47 s
Description: Du fragst dich, was es mit dem Wärmeübergangskoeffizienten auf sich hat? Dann bist du hier genau richtig!

Du fragst dich, was es mit dem Wärmeübergangskoeffizienten auf sich hat? Dann bist du hier genau richtig!

Inhaltsübersicht

Wärmeübergangskoeffizient einfach erklärt

Der Wärmeübergangskoeffizient h oder $\alpha$ ist ein Proportionalitätsfaktor für den Wärmeübergang an einer Grenzfläche. Sein Kehrwert ist der Wärmeübergangswiderstand R_s. Wenn du nicht mehr so richtig weißt, um was es sich beim Wärmeübergangswiderstand handelt, kannst du dir unseren Beitrag dazu nochmal durchlesen.

Wärmeübergangskoeffizient - Definition — Wärmeübergangskoeffizient – Definition

Der Wärmeübergangskoeffizient wird in $\frac{W}{m^2K}$ angegeben.

Merke

Je höher der Wärmeübergangskoeffizient, desto schlechter die Wärmedämmeigenschaften der Stoffgrenze.

Anwendung findet der Wärmeübergangskoeffizient beispielsweise in der Berechnung der übertragenen Wärmemenge mit der Formel:

$Q=h \cdot A \cdot (T_1 - T_2) \cdot \Delta t$

Kontaktfläche: A
Differenz der Stofftemperatur:
Zeitintervall: $\Delta t$

Bei den Wärmeübergangskoeffizienten unterscheidet man zwischen dem lokalen, dem mittleren Koeffizienten sowie den Wärmeübergangskoeffizienten bei Konvektion und freier Wärmestrahlung . Schauen wir uns zuerst den lokalen Wärmeübergangskoeffizienten an.

Lokaler Wärmeübergangskoeffizient

Lokale Wärmeübergangskoeffizienten finden beispielsweise Anwendung in der computergestützten Simulation. Da für dünne Grenzschichten die Strömung an der Bauteiloberfläche laminar ist, erfolgt der Wärmetransport überwiegend durch Wärmeleitung.

Du ermittelst den lokalen Wärmeübergangskoeffizient h aus der Wärmeleitfähigkeit λ des Fluids bei der mittleren Temperatur $\frac{T_1 + T_2}{2}$ und der Dicke d_t der thermischen Grenzschicht. Somit folgt:

$\alpha = \frac{\lambda}{d_t}$

Willst du die lokale Wärmestromdichte durch die Grenzschicht $\.q_G_S$ bestimmen, gilt:

$\.q_G_S = \alpha \cdot (T_1 - T_2)$

Lokaler Wärmeübergangskoeffizient - Berechnung — Lokaler Wärmeübergangskoeffizient – Berechnung

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Mittlerer Wärmeübergangskoeffizient

Der mittlere Wärmeübergangskoeffizient a_m wird meistens für technische Berechnungen verwendet. Dieser ist dann für bestimmte Geometrien und in Abhängigkeit von der Temperatur des Fluids am Einlauf und der mittleren Wandtemperatur definiert.

a_m ist proportional zur Nusselt-Zahl oder auch Nu-Zahl, welche wiederum als eine Funktion der Reynolds-Zahl und der Prandtl-Zahl angegeben ist. Du möchtest dir nochmal in Ruhe anschauen, was diese dimensionslosen Kennzahlen bedeuten und was sie beschreiben? In unserem Beitrag zum konvektiven Wärmeübergang wird genau das erklärt!

Für a_m gilt:

$a_m = \frac{\lambda}{L} \cdot Nu(Re,Pr)$

L: charakteristische Länge
$\lambda$ : Wärmeleitfähigkeit des Fluids
Re: Reynolds-Zahl
Pr: Prandtl-Zahl

Da die Nusselt-Zahl eine Funktion der dimensionslosen Reynolds- und Prandtl-Zahl ist, setzt sie sich auch aus diesen zusammen.

Zum einen bedienen wir uns der Reynolds-Zahl mit der Formel

$Re = \frac{p \cdot v \cdot L}{\eta}$

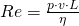
Zum anderen wird die Prandtl-Zahl benötigt. Für diese gilt

$Pr = \frac{\eta \cdot c_p}{\lambda}$

p: Dichte bei der arithmetisch gemittelten Temperatur des Fluides
v: Strömungsgeschwindigkeit
L: charakteristische Länge
$\eta$ : dynamische Viskosität des Fluids
: isobare spezifische Wärmekapazität

Freie Konvektion

Sobald die Strömung durch freie Konvektion bedingt ist, hängt die Nusselt-Zahl von der Grashof-Zahl ab. Zur Berechnung des Wärmeübergangskoeffizenten $\alpha$ kannst du dann folgende Näherungsformeln verwenden.

Ist dein verwendetes Fluid Luft, dann gilt

$\alpha = 2 + 12 \cdot \sqrt{v}$

Für verschiedene exemplarische Windgeschwindigkeiten ergeben sich folgende Werte für den äußeren Wärmeübergangswiderstand:

Äußerer Wärmeübergangskoeffizient - Berechnung — Äußerer Wärmeübergangskoeffizient – Berechnung

Dabei kannst du dir Folgendes merken: Je höher die Windgeschwindigkeiten, desto geringer die äußeren Wärmeübergangswiderstände.

Ist dein verwendetes Fluid Wasser, lautet die Formel

$\alpha = 580 + 2100 \cdot \sqrt{v}$

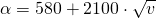
Aber beachte: In diesen beiden Fällen musst du die Geschwindigkeit v in der Einheit $\frac{m}{s}$ einsetzen.

Wärmeübergang durch Wärmestrahlung

Die Berechnung des Wärmeübergangskoeffizienten bei Wärmestrahlung ist sehr komplex. Für einen idealen schwarzen Körper gelten die Werte in der folgenden Tabelle:

Temperatur in °C	-10	0	10	20	30
h_s0 in W/m²K	4,1	4,6	5,1	5,7	6,3
R_se	0,24	0,22	0,2	0,18	0,16

Super! Damit kennst du jetzt den lokalen und mittleren Wärmeübergangskoeffizienten, sowie die Koeffizienten für die freie Konvektion und den Wärmeübergang durch Strahlung.

Wärmeübergangskoeffizient — häufigste Fragen

(ausklappen)

Was versteht man unter Wärmeübergang?

Wärmeübergang ist die Übertragung von Wärmeenergie über eine Grenzfläche zwischen zwei Systemen oder Stoffen mit unterschiedlicher Temperatur. An der Grenzfläche fließt Wärme vom höheren zum niedrigeren Temperaturniveau, bis sich die Temperaturen annähern. Der Wärmeübergang kann je nach Situation durch Leitung, Konvektion oder Strahlung geprägt sein.
Wie berechnet man den Wärmeübergangskoeffizienten?

Den Wärmeübergangskoeffizienten $h/\alpha$ berechnet man aus einer passenden Wärmeübergangs-Beziehung, zum Beispiel aus $Q = h \cdot A \cdot (T_1 - T_2) \cdot \Delta t$ durch Umstellen zu $h = \dfrac{Q}{A\,\Delta T\,\Delta t}$ . Konkret: $Q = 2{,}0 \cdot 10^4\,\text{J}$ , $A = 2\,\text{m}^2$ , $\Delta T = 10\,\text{K}$ , $\Delta t = 100\,\text{s}$ ergibt $h = 10\,\frac{\text{W}}{\text{m}^2\cdot\text{K}}$ .
Was ist der Unterschied zwischen lokalem und mittlerem Wärmeübergangskoeffizienten?

Der lokale Wärmeübergangskoeffizient beschreibt den Wärmeübergang an einem bestimmten Ort der Oberfläche und kann sich entlang der Fläche ändern. Der mittlere Wärmeübergangskoeffizient fasst den Wärmeübergang über eine ganze Fläche oder eine charakteristische Länge zu einem einzigen Ersatzwert zusammen. Deshalb nutzt man lokal eher für detaillierte Profile und mittel eher für technische Überschlagsrechnungen.
Warum bedeutet ein hoher Wärmeübergangskoeffizient eine schlechtere Wärmedämmung?

Ein hoher Wärmeübergangskoeffizient bedeutet eine schlechtere Wärmedämmung, weil bei gleichem Temperaturunterschied mehr Wärme pro Fläche und Zeit durch die Stoffgrenze übertragen wird. Mathematisch ist der zugehörige Wärmeübergangswiderstand der Kehrwert, also $R_s = \dfrac{1}{h}$ . Ein größeres entspricht deshalb einem kleineren Widerstand.

Wärmeübertragung verstehen

Der Wärmeübergangskoeffizient gehört zur Wärmeübertragung und beschreibt den Wärmeaustausch an einer Grenzfläche. Wer sich mit Wärmeübertragung beschäftigt, vergleicht Wärmeleitung, Konvektion und Strahlung in technischen Systemen. Dabei wird klar, wie Stoffwerte, Strömung und Geometrie den Wärmestrom beeinflussen. Im Ingenieurwissenschaftenbereich findest du passende Videos zu diesem und verwandten Themen.

zur Videoseite: Wärmeübergangskoeffizient