Wärmestrahlung
Was verstehst du unter Wärmestrahlung, was sind ihre Eigenschaften und welche Bedeutung hat sie? Das erfährst du hier in unserem Beitrag und im Video .
Inhaltsübersicht
Was ist Wärmestrahlung?
Die Wärmestrahlung ist neben der Konvektion und der Konduktion eine weitere Art der Wärmeübertragung. Hierbei wird Wärme durch elektromagnetische Wellen übertragen. Als Beispiele kannst du dir infrarote Strahlung oder infrarotes Licht vorstellen.
Im Unterschied zur Wärmeleitung und Wärmeströmung braucht die Wärmestrahlung kein Medium (z.B. Metall), um sich auszubreiten. Sie breitet sich auch im Vakuum (z.B. Weltraum) aus. Ihre Hauptquelle ist die Sonne.
Die Wärmestrahlung kann von einem Körper aufgenommen (absorbiert), zurückgeworfen (reflektiert) oder durchgelassen werden. Wenn ein Körper die Strahlen aufnimmt, erwärmt er sich. Deshalb steigt seine Temperatur. Genauer gesagt, wird dann die Strahlungsenergie in Wärmeenergie umgewandelt.
Der Begriff „infrarote Strahlung“ kommt daher, weil die Wärmestrahlung an den Wellenlängen des roten Lichts angrenzt.
Eigenschaften der Wärmestrahlung
Die Wärmestrahlung oder auch Temperaturstrahlung nimmst du nicht als Licht wahr. Du kannst sie nur durch ihre Wirkung auf uns Menschen beziehungsweise die uns umgebenden Stoffe bemerken. Denn sie verändern dadurch ihre Temperatur. Im Sommer spürst du beispielsweise die Wärme der Sonne, die von deiner Haut oder auch von deinem schwarzen T-Shirt aufgenommen wird.
Dabei geht sie größtenteils von der Sonne aus. Die Sonnenstrahlung setzt sich jedoch aus unterschiedlichen Bestandteilen zusammen:
- Sichtbares Licht: 50%
- Wärmestrahlung: 40%
- UV-Strahlung: 5%
- Andere Strahlungsarten: 5%
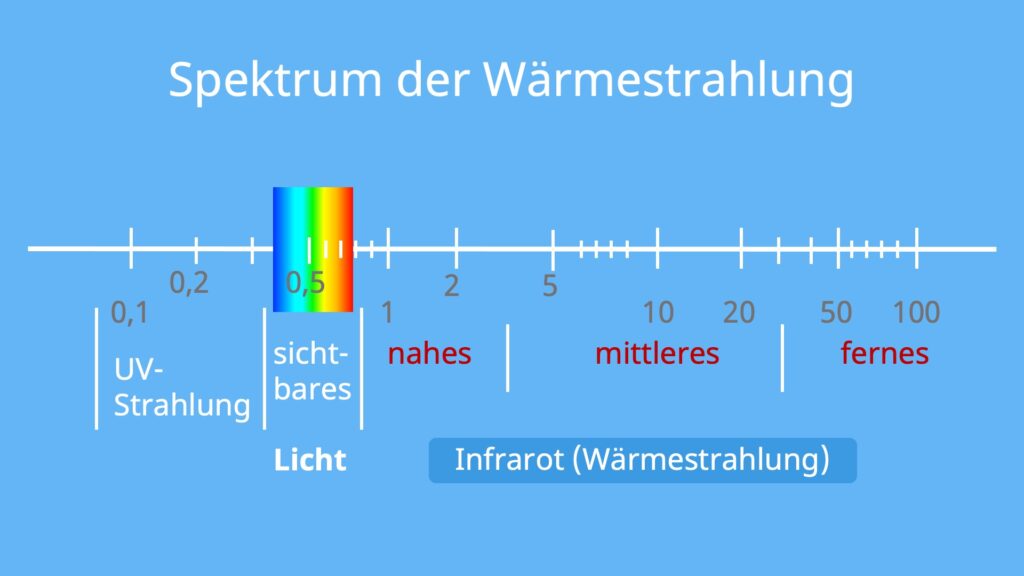
Das sichtbare Licht befindet sich in einem Wellenlängenbereich von 0,4 – 0,8 μm (Mikrometer). Als Wärmestrahlung kannst du die Wellen in einem Bereich von 0,8 – 100 μm benennen. Je länger die Wellen sind, desto geringer ist deren Energie. Somit besitzt die infrarote Strahlung (angrenzend am sichtbaren, roten Licht) die geringste Energie.
Aber nicht nur die Sonne gibt Temperaturstrahlung ab. Durch Infrarotlampen oder Infrarotstrahler kannst du sie ebenfalls erzeugen. Auch Glühlampen, Öfen und sogar dein Körper geben Energie in Form von Wärmestrahlung ab. Dabei gilt: Je wärmer der Körper ist, desto stärker ist die Temperaturstrahlung, die von ihm ausgeht.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Aufnahme der Wärmestrahlung
Wenn Wärmestrahlung auf einen Körper trifft, kann sie reflektiert (zurückgeworfen), absorbiert (aufgenommen) oder teilweise durchgelassen werden. Dabei spielt der Stoff, die Dicke und die Oberflächenbeschaffenheit des Körpers eine wichtige Rolle.
| Eigenschaft des Körpers | Auswirkungen auf die Wärmestrahlung | Beispiele |
| dunkel, rau | viel absorbiert, wenig reflektiert | dunkle Kleidung, Solarplatten (raue, schwarze Flächen) |
| hell, glatt | wenig absorbiert, viel reflektiert | helle Kleidung, Kühl- und Tankwagen (oft helle Lackierungen) |
Bei zwei Körpern mit der gleichen Temperatur strahlt derjenige mit dunkler Oberfläche stärker, als der mit weißer Oberfläche. Durch die hohe Absorption kann der Körper wiederum selbst Wärme abstrahlen.
Wärmestrahlung im Alltag
Für die Wärmestrahlung gibt es verschiedenste Anwendungsbereiche. Im Folgenden siehst du einige Beispiele:
- Solarplatten: Hierbei wird die von der Sonne ausgesendete Temperaturstrahlung aufgenommen. Dadurch ist es dann möglich, elektrische Energie zu erzeugen.
- Infrarotlampen/Infrarotstrahler: Sie geben Wärme in Form von Strahlen selbst ab. Dabei finden sie vor allem Anwendung im medizinischen Bereich, wie z. B. zur Linderung von Entzündungen oder Muskelschmerzen. Zusätzlich sorgen sie aber auch dafür, Räume mit genügend Wärme zu versorgen (z. B. im Bereich der Tierzucht).
Allerdings ist die Wärmestrahlung auch teilweise unerwünscht und muss vermieden werden.
- Heiße Getränke in Thermoskannen: Hier ist eine Ausstrahlung von Wärme eher unerwünscht. Damit dein Getränk also nicht so schnell kalt wird, besitzt die Thermoskanne mehrere Schichten. So wird die Temperaturstrahlung, die vom Getränk ausgeht, wieder nach innen reflektiert.
- Kühl- und Tankwagen: Auch dort ist eine intensive Temperaturstrahlung der Sonne eher ungünstig und sollte vermieden werden. Damit nur wenig der Strahlung absorbiert wird, sind die Oberflächen oft glatt und hell. So kann eine schnelle Erwärmung verhindert werden.
Elektromagnetisches Spektrum
Die Wärmestrahlung besteht aus elektromagnetischen Wellen eines ganz bestimmten Wellenlängenbereichs. Sie ist somit ein Bestandteil des elektromagnetischen Spektrums. Wenn du noch mehr über das elektromagnetische Spektrum und seine Unterteilung wissen möchtest, schau dir unser Video dazu an.