Histogramm
Du fragst dich, was ein Histogramm ist und wie man es erstellt? In diesem Artikel erklären wir dir es leicht verständlich anhand anschaulicher Beispiele!
Du möchtest das Thema noch schneller verstehen? Dann sieh dir jetzt unser Lernvideo an! Hier bekommst du alles, was du wissen musst, in nur wenigen Minuten perfekt aufbereitet.
Inhaltsübersicht
Histogramm einfach erklärt
Ein Histogramm ist eine Grafik, in der du Häufigkeiten oder die Häufigkeitsdichte bestimmter Ausprägungen einer Variable ablesen kannst. Trotz der Ähnlichkeit handelt es sich hierbei nicht um ein Säulendiagramm . Bei einem Säulendiagramm liegen die Daten bereits von vorneherein gruppiert vor ( z.B. „männlich“, „weiblich“, „divers“), bei einem Histogramm müssen sie hingegen erst in Gruppen eingeteilt werden (z.B. Einteilung des Alters in 10-Jahres-Klassen). Die verschiedenen Gruppen werden anschließend nebeneinander in Rechtecken dargestellt. Du kannst dabei entscheiden, ob du die absolute oder die relative Häufigkeit der Merkmalsgruppen in deinem Histogramm abbildest.
- Die Höhe der Rechtecke gibt Auskunft über die Anzahl der Messwerte in einer Gruppe. Stellst du in deinem Histogramm relative Häufigkeiten dar, kannst du hier die Häufigkeitsdichte dieser Gruppe ablesen.
- Die Breite der Rechtecke sagt dir, welches Intervall in diese Gruppe fällt, also etwa, dass dieses Rechteck die Gruppe der 20 bis 30-Jährigen darstellt
- Der Flächeninhalt dieser Rechtecke ist von Bedeutung, wenn du in deinem Histogramm relative Häufigkeiten darstellst. In diesem Fall sagt dir der Flächeninhalt des Rechtecks, wie viele Messwerte in diese Gruppe fallen.
Histogramm erstellen
Möchtest du ein Histogramm erstellen, benötigst du die Häufigkeitsverteilung eines kontinuierlichen Merkmals. Das bedeutet, du musst wissen, welche Merkmale wie häufig vorliegen.
Bevor du das Histogramm erstellst, musst du die verschiedenen Ausprägungen der Variable zunächst in Gruppen bzw. Klassen unterteilen. Dafür legst du fest, wie breit die Intervalle sein sollen, die jeweils eine Gruppe bilden sollen. Du könntest etwa festlegen, dass bei der Variable „Alter“ immer 10 Jahre eine Klasse bilden sollen. Wie du die Klassen genau einteilst, bleibt dir selbst überlassen. Diese Einteilung legt fest, wie breit die Rechtecke deines Histogramms später sein sollen. Du kannst dabei entscheiden, ob die Gruppen gleich oder verschieden breit sein sollen.
Anschließend bestimmst du die absolute Klassenhäufigkeit  . Dafür zählst du ab, wie viele Messwerte jeweils in diese Klasse fallen.
. Dafür zählst du ab, wie viele Messwerte jeweils in diese Klasse fallen.
Mit Hilfe der Breite deiner Klasse 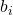 und der absoluten Klassenhäufigkeit
und der absoluten Klassenhäufigkeit  kannst du die Höhe eines Rechecks
kannst du die Höhe eines Rechecks  mit folgender Formel berechnen:
mit folgender Formel berechnen:

 : Höhe des i-ten Rechtecks (Häufigkeitsdichte)
: Höhe des i-ten Rechtecks (Häufigkeitsdichte)
 : Anzahl der Messwerte der i-ten Klasse (Klassenhäufigkeit)
: Anzahl der Messwerte der i-ten Klasse (Klassenhäufigkeit)
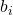 : Breite der i-ten Klasse (Klassenbreite)
: Breite der i-ten Klasse (Klassenbreite)
Die Formel für die Häufigkeitsdichte leitet sich aus der Formel zur Berechnung des Flächeninhalts eines Rechtecks her. Um den Flächeninhalt zu bestimmen, rechnest du Höhe mal Breite. Da wir den Flächeninhalt (die Klassenhäufigkeit) jedoch schon kennen und die Höhe berechnen wollen, stellen wir die Formel einfach um und erhalten die obige Formel.
Manchmal begegnet dir auch diese Formel:

mit 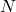 : Gesamtzahl der Messwerte
: Gesamtzahl der Messwerte
Sie wird verwendet, wenn du die relativen Häufigkeiten berechnen möchtest. Die Klassenhäufigkeit wird deshalb nochmal durch die Gesamtzahl der Nennungen geteilt. Als Ergebnis erhältst du also, statt der absoluten, die relative Häufigkeitsdichte.
Wenn du schließlich alle Werte ermittelt hast, kannst du das Histogramm zeichnen.
Beispiel gleiche Klassenbreite
In de Praxis erstellst du ein Histogramm dann folgendermaßen: Das betrachtete Merkmal ist das Alter von 20 Personen. Für das Histogramm werden fünf gleich große Klassen gebildet. Die Klassenbreite bi ist deshalb überall 10. In der letzten Spalte erkennst du die Anzahl der Personen in der jeweiligen Klasse.
| Klasse i | Alter xi | Klassenbreite bi | Anzahl der Personen ni |
| 1 | 0 bis unter 10 | 10 | 2 |
| 2 | 10 bis unter 20 | 10 | 5 |
| 3 | 20 bis unter 30 | 10 | 3 |
| 4 | 30 bis unter 40 | 10 | 6 |
| 5 | 40 bis unter 50 | 10 | 4 |
Um nun die Höhe hi zu berechnen, setzt du die Werte aus Spalte drei und vier einfach in die Formel für die absolute Häufigkeitsdichte ein. Für die erste Klasse sieht das so aus:

Berechnest du das für alle Klassen, erhältst du in der Tabelle folgende zusätzliche Spalte:
| Klasse i | Alter xi | Klassenbreite bi | Anzahl der Personen ni | hi (ni/bi) |
| 1 | 0 bis unter 10 | 10 | 2 | 0,2 |
| 2 | 10 bis unter 20 | 10 | 5 | 0,5 |
| 3 | 20 bis unter 30 | 10 | 3 | 0,3 |
| 4 | 30 bis unter 40 | 10 | 6 | 0,6 |
| 5 | 40 bis unter 50 | 10 | 4 | 0,4 |
Nun kannst du das Histogramm zeichnen. Bei gleicher Klassenbreite ist das sowohl mit der absoluten Häufigkeit, als auch mit der Häufigkeitsdichte möglich. Damit ergeben sich die zwei folgenden Histogramme:
Im linken Diagramm kannst du die Klassenhäufigkeit einfach an der y-Achse ablesen. Dies ist allerdings nur bei gleicher Klassenbreite möglich. Im rechten Diagramm entspricht die Anzahl der Personen pro Gruppe dem Flächeninhalt des Rechtecks. So sind beispielsweise in Klasse 4 (Personen im Alter von 30 bis 40 Jahren)  also 6 Personen enthalten.
also 6 Personen enthalten.
Solltest du die Formel mit der relativen Häufigkeit verwendet haben, stellt der Flächeninhalt eines Rechtecks den prozentualen Anteil der Klasse an der Gesamtzahl dar. Probiers‘ doch mal aus.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel variable Klassenbreite
Nun kann es aber auch sein, dass die gewählten Gruppen eine unterschiedliche Breite besitzen. Dies ist zum Beispiel bei gesellschaftlichen Generationen der Fall. Hier kann man drei Klassen definieren:
- Babyboomer: 1955 bis ausschließlich 1970
- Generation X: 1970 bis ausschließlich 1980
- Generation Y: 1980 bis ausschließlich 2000
Erneut werden 20 Personen betrachtet und den Klassen zugeordnet. Damit ergibt sich folgende Tabelle:
| Klasse i | Geburtsjahr der Person xi | Klassenbreite bi | Anzahl der Personen ni |
| 1 (Babyboomer) | 1955 bis unter 1970 | 15 | 3 |
| 2 (Gen X) | 1970 bis unter 1980 | 10 | 7 |
| 3 (Gen Y) | 1980 bis unter 2000 | 20 | 10 |
Wendest du erneut die Formel an, erhältst du diese Höhen hi:
| Klasse i | Geburtsjahr der Person xi | Klassenbreite bi | Anzahl der Personen ni | hi (ni/bi) |
| 1 (Babyboomer) | 1955 bis unter 1970 | 15 | 3 | 0,2 |
| 2 (Gen X) | 1970 bis unter 1980 | 10 | 7 | 0,7 |
| 3 (Gen Y) | 1980 bis unter 2000 | 20 | 10 | 0,5 |
Hier ist es nun wichtig, das Histogramm mittels der Dichte darzustellen, da eine Darstellung mit absoluten Häufigkeiten zu einem fälschlichen Ergebnis führt.Selbstverständlich lässt sich auch hier die Formel der relativen Häufigkeitsdichte anwenden. Dazu teilst du die bereits berechnete Häufigkeitsdichte durch die Anzahl an Personen, in diesem Beispiel also 20.
Berechnest du den Flächeninhalt eines der Rechtecke, erhältst du, wie im vorherigen Beispiel, die Personenanzahl aus der jeweiligen Gruppe.
Histogramm zeichnen
Um ein Histogramm darzustellen, kannst du Tabellenkalkulationsprogramme wie Excel verwenden oder es einfach selbst zeichnen. Dabei musst du auf eine geeignete Skalierung und eine maßstabsgetreue Beschriftung der Achsen achten.
Bei variablen Klassenbreiten musst du außerdem auf die korrekte Breite der jeweiligen Klasse achten. Nur so lässt sich später auch der Flächeninhalt und somit die Klassenhäufigkeit graphisch ermitteln. Die gezeichneten Rechtecke (Klassen) grenzen, im Gegensatz zum Säulendiagramm, immer direkt aneinander.
Histogramm — häufigste Fragen
(ausklappen)
Histogramm — häufigste Fragen
(ausklappen)-
Was ist ein Histogramm?Ein Histogramm ist eine Grafik, in der du Häufigkeiten oder die Häufigkeitsdichte von Merkmalsausprägungen ablesen kannst. Dafür teilst du die Werte zuerst in Klassen (Intervalle) ein. Jede Klasse wird als Rechteck dargestellt, und die Rechtecke liegen direkt nebeneinander.
-
Wie unterscheidet sich ein Histogramm von einem Säulendiagramm?Ein Histogramm nutzt Klassen, die du aus den Rohdaten erst bilden musst, ein Säulendiagramm hat meist schon fertige Kategorien. Außerdem grenzen die Rechtecke im Histogramm direkt aneinander. Beim Säulendiagramm stehen die Säulen typischerweise für getrennte Gruppen wie „männlich“ oder „weiblich“.
-
Wie entscheide ich, wie ich meine Daten in Klassen einteile?Du legst die Klassen selbst fest, indem du entscheidest, wie breit die Intervalle sein sollen. Diese Klassenbreite bestimmt später die Breite der Rechtecke im Histogramm. Zum Beispiel kannst du beim Merkmal „Alter“ 10-Jahres-Klassen wählen, also 20 bis unter 30, 30 bis unter 40 usw.
-
Wie berechne ich die Höhe eines Rechtecks im Histogramm?Die Höhe berechnest du mit
 . Dabei ist
. Dabei ist  die Anzahl der Messwerte in Klasse
die Anzahl der Messwerte in Klasse  und
und  die Klassenbreite. Diese Höhe heißt Häufigkeitsdichte. Im Beispiel gilt für 0 bis unter 10:
die Klassenbreite. Diese Höhe heißt Häufigkeitsdichte. Im Beispiel gilt für 0 bis unter 10:  .
.
-
Wann muss ich im Histogramm mit Häufigkeitsdichte statt mit absoluter Häufigkeit arbeiten?Bei unterschiedlich breiten Klassen musst du mit Häufigkeitsdichte arbeiten, sonst wirkt das Ergebnis falsch. Dann zählt nicht die Balkenhöhe allein, sondern die Fläche des Rechtecks. Im Beispiel mit Babyboomern, Gen X und Gen Y haben die Klassen verschiedene Breiten, deshalb wird über die Dichte dargestellt.


