Konvektiver Wärmeübergang mit Reynoldszahl, Nusselt-Zahl, Prandtl-Zahl und Grashof-Zahl
Du hast dich schon immer gefragt, wieso ein Glas, in dem Eiswürfel sind, außen auch nass ist? Die Antwort darauf hat mit dem konvektiven Wärmeübergang zu tun, für dessen Berechnung du die Reynoldszahl, die Nusselt-Zahl, die Prandtl-Zahl und die Grashof-Zahl benötigst. Die Formeln sowie die Berechnung des konvektiven Wärmeübergangs erklären wir dir im Folgenden.
Inhaltsübersicht
Was bedeutet konvektiver Wärmeübergang und was sind die Reynoldszahl, Nusselt-Zahl, Prandtl-Zahl und Grashof-Zahl?
Zuerst einmal solltest du dich daran erinnern, dass bestimmte Körper Wärme leiten können und ein Wärmetransport immer dann stattfindet, wenn es einen Temperaturunterschied gibt. Auch Fluide sind wärmeleitfähig. Wenn du also eine kalte Flüssigkeit, zum Beispiel Eiswasser, in ein Glas gibst, dessen Oberfläche genauso warm ist wie die Umgebungstemperatur, dann findet ein Wärmetransport statt. Während das Wasser wärmer wird, wird das Glas kälter und es bilden sich Kondensationstropfen am Glas.
Konvektiver Wärmeübergang
Doch was steckt da genau dahinter? Das ist der sogenannte konvektive Wärmeübergang. Bei der Konvektion wird noch einmal zwischen natürlicher und erzwungener Konvektion unterschieden. Vorerst begnügen wir uns allerdings mit dem konvektiven Wärmeübergang.
Noch mal zur Erinnerung: Konvektion bedeutet Wärmeübertragung von einer Festkörperoberfläche an ein anliegendes Fluid oder anders herum. Für die Berechnung des Wärmeübergangs werden einige dimensionslose Kennzahlen, also Zahlen ohne Einheiten, gebraucht.
Grashof-Zahl
Nun, da du die Reynoldszahl kennst, kommen wir zur zweiten Zahl, der Grashof-Zahl Gr, die das Verhältnis von Auftriebskraft zur Reibungskraft darstellt. Die Grashof-Zahl wird mit 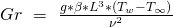 berechnet.
berechnet. 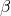 ist der sogenannte thermische isobare Ausdehnungskoeffizient und kann mit der Formel
ist der sogenannte thermische isobare Ausdehnungskoeffizient und kann mit der Formel 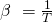 berechnet werden.
berechnet werden.
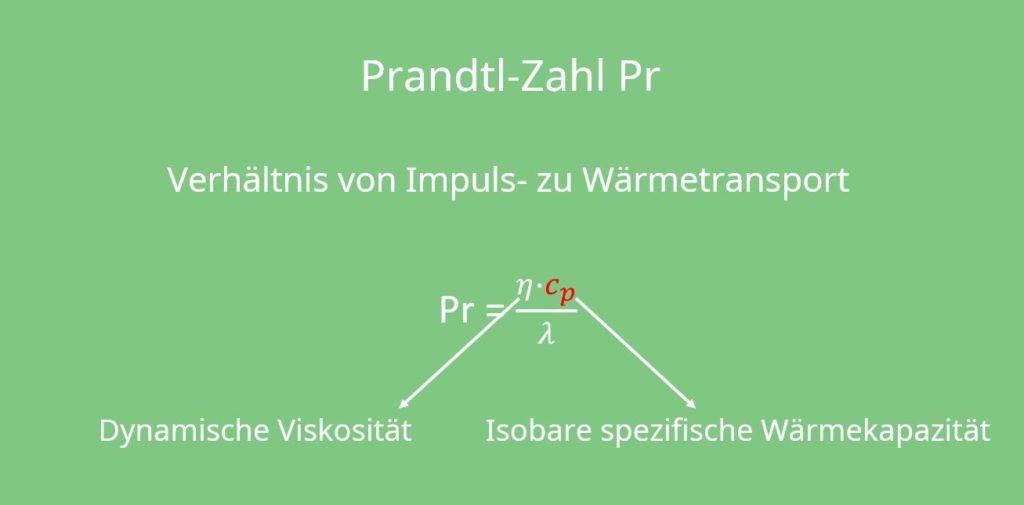
Prandtl-Zahl
Neben der Reynoldszahl und der Grashof-Zahl benötigt man für die Berechnung des konvektiven Wärmeübergangs auch die Prandtl-Zahl Pr, die das Verhältnis von Impuls- zu Wärmetransport darstellt und nur Stoffgrößen enthält, die aus einer Tabelle entnommen werden können. Die Formel für die Prandtl-Zahl lautet 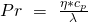 . Dabei ist
. Dabei ist 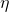 die dynamische Viskosität und
die dynamische Viskosität und 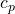 die isobare spezifische Wärmekapazität.
die isobare spezifische Wärmekapazität.
Nusselt-Zahl
Die Nusselt-Zahl Nu ist neben der Reynoldszahl, der Grashof-Zahl und der Prandtl-Zahl die vierte Kennzahl. Sie zeigt das Verhältnis des Wärmestroms infolge von Konvektion zum Wärmestrom infolge von Leitung. Das heißt: Da der Wärmeübergang zum einen aufgrund von Konvektion und zum anderen rein durch die Wärmeleitung erfolgen kann, wird mit Hilfe der Nusselt-Zahl das Verhältnis der beiden Vorgänge beschrieben. Die Nusselt-Zahl wird berechnet mit 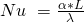 .
.
Die letzten beiden dimensionslosen Kennzahlen sind zusammengesetzte Kennzahlen, da sie Zusammenstellungen aus der Reynoldszahl, der Grashof-Zahl, der Prandtl-Zahl und der Nusselt-Zahl sind.
Konvektiver Wärmeübergang – Charakteristische Länge
Du wirst dich jetzt sicher fragen, was genau das 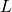 in den Formeln der Reynoldszahl, Grashof-Zahl, Prandtl-Zahl und Nusselt-Zahl ist.
in den Formeln der Reynoldszahl, Grashof-Zahl, Prandtl-Zahl und Nusselt-Zahl ist. 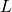 ist die sogenannte charakteristische Länge, die sich je nach Strömungsfall anders berechnen lässt. Wir werden dir hier nur die allgemeine Herangehensweise erklären, die sich in die Gebiete Durchströmung und Umströmung unterscheiden lässt. Bei einer Durchströmung eines rechteckigen Kanals wird
ist die sogenannte charakteristische Länge, die sich je nach Strömungsfall anders berechnen lässt. Wir werden dir hier nur die allgemeine Herangehensweise erklären, die sich in die Gebiete Durchströmung und Umströmung unterscheiden lässt. Bei einer Durchströmung eines rechteckigen Kanals wird 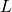 zu
zu 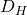 mit
mit 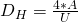 und bei Durchströmung eines runden Rohres lautet die Formel
und bei Durchströmung eines runden Rohres lautet die Formel 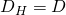 , also gleich dem Rohrinnendurchmesser. Bei der Umströmung ist
, also gleich dem Rohrinnendurchmesser. Bei der Umströmung ist 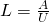 . Wenn eine ebene Platte umströmt wird, haben wir einen Sonderfall, bei dem
. Wenn eine ebene Platte umströmt wird, haben wir einen Sonderfall, bei dem 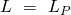 ist, also die Länge der Platte.
ist, also die Länge der Platte.
Konvektiver Wärmeübergang – Bezugstemperatur
Nicht nur die Länge ist abhängig von der Strömungsart, sondern auch die Temperatur. Wird ein Körper umströmt, haben wir die Bezugstemperatur 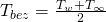 . Wird der Körper durchströmt, lautet die Formel
. Wird der Körper durchströmt, lautet die Formel 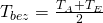 , wobei
, wobei 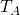 die Temperatur am Austritt und
die Temperatur am Austritt und 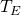 die Temperatur am Eintritt beschreibt.
die Temperatur am Eintritt beschreibt.
Jetzt weißt du, was der konvektive Wärmeübergang damit zu tun hat, dass dein Glas mit Eiswürfeln auch außen nass ist. Zudem kannst du den konvektiven Wärmeübergang jetzt sogar mithilfe der Reynoldszahl, Grashof-Zahl, Prandtl-Zahl und Nusselt-Zahl berechnen.
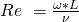 .
. 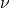 ist die kinematische Viskosität des Fluides.
ist die kinematische Viskosität des Fluides. 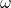 ist die Bezugsgeschwindigkeit und wird je nach Fall unterschiedlich berechnet.
ist die Bezugsgeschwindigkeit und wird je nach Fall unterschiedlich berechnet.