Torsion – Verdrillung
Bei einer Torsion wirkt eine Kraft auf einen Körper und verdreht diesen. In diesem Artikel erklären wir dir dieses Thema genauer.
Du möchtest alles kurz und knapp in einem Video sehen? Dann schau doch hier mal rein.
Inhaltsübersicht
Torsion einfach erklärt
Bei einer Torsion verdreht sich der Körper. Die Kraft wirkt dabei über einen Hebel und wird Torsionsmoment genannt. Dieses Moment erzeugt in dem Objekt Spannungen, welche als Torsionsspannungen bezeichnet werden. Die Spannungen, die bei diesem Vorgang entstehen sind Schubspannungen . Neben diesen Größen tritt bei Torsion noch eine andere wichtige auf. Diese wird als Drillung bezeichnet und ist definiert als „Verschiebewinkel pro Flächeneinheit“. Sie gibt also die Stärke der Verdrehung durch ein Torsionsmoment an.
Verdrillung berechnen
Die Drillung betrachten wir am Beispiel eines dünnwandigen Rohres. Für kreisrunde Querschnitte gilt:

Wir müssen den Term also nur noch durch r und L teilen und setzen für Tau die erste Bredt’sche Formel „tau gleich M T durch 2 t mal A“ ein. Mit dem Flächeninhalt „A gleich Pi mal r Quadrat“ erhalten wir:

Zufällig ergibt sich das Polare Flächenträgheitsmoment eines dünnwandigen Rohres genau zu „zwei t Pi r hoch drei“. Das heißt, das polare Flächenträgheitsmoment ist der geometrische Widerstand gegen Torsion. Damit ergibt sich:

Wir wollen jetzt für unser Rohr die Verdrillung bestimmen. Die Dicke beträgt fünf Millimeter, der Wert des Durchmessers ist 300 Millimeter und das Moment 20 KilonewtonMillimeter. Die einzige Größe, die wir noch benötigen, ist der Schubmodul G. Das heißt wir brauchen noch das Material. Wir nehmen einfach an, wir betrachten Stahl mit einem Schubmodul von 80.000 Megapascal.
Wir müssen jetzt nur noch einsetzen und erhalten für die Drillung:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Verdrillung bei nicht konstanter Umfangsdicke
Für ein dünnwandiges Rohr mit variierender Umfangsdicke können wir die Verdrillung nicht so einfach herleiten. Hier nutzen wir den Zusammenhang, dass die äußere Arbeit gleich der inneren Arbeit sein muss. Die äußere Arbeit wird durch das Moment geleistet und ist definiert durch:

Die innere Arbeit definiert sich über die Spannung zu:
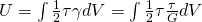
Das Volumenelement können wir auch wieder vereinfachen. Es setzt sich aus der Länge, der Profildicke und dem Umfang zusammen. Wir betrachten aber nur einen infinitesimalen Teil des Umfangs. Dadurch erhalten wir für das Volumenelement:

Zusätzlich können wir wieder tau mit Hilfe der ersten Bredt’schen Formel ersetzen. Setzen wir das Ganze in die innere Arbeit ein ergibt sich:

Anschließend setzen wir dies mit der äußeren Arbeit gleich und vereinfachen:

Wir müssen jetzt also nur noch nach Fi durch L umformen. Doch was heißt dieses Ringintegral? Es sagt einfach nur aus, dass wir mit unser Laufkoordinate einmal im Kreis laufen und wieder da ankommen wo wir angefangen haben. Daher auch der Name Ringintegral. Für unseren Fall heißt das, dass wir einfach den ganzen Querschnitt entlanglaufen. Nun müssen wir nur noch nach Fi durch L umformen und erhalten für die Drillung:

Dabei nutzen wir aus, dass der Schubfluss, also Tau mal t, konstant ist. Es ergibt sich:

Das heißt die Drillung ist alleine abhängig von der Profildicke, da der Schubfluss konstant ist.
Ringintegrale auflösen
Das Ringintegral können wir in der Regel nochmal umschreiben, da wir oft Abschnitte haben, bei denen die Profildicke über einen bestimmen Bereich konstant ist. Um dir zu zeigen, wie das genau geht, betrachten wir ein Rechteckprofil mit der Höhe h gleich 10 Zentimeter und der Breite b gleich 25 Zentimeter. Das Rechteckprofil hat auf der linken und rechten Seite die Profildicke t gleich 5 Millimeter und oben und unten die Profildicke zwei t.
Wenn wir uns überlegen, dass das Ringintegral einmal der Kontur folgt und eigentlich nur eine Summe über infinitesimal kleine Abstände ist, können wir es umschreiben zu:

Das heißt wir teilen uns den Querschnitt in einzelne Abschnitte mit der jeweiligen Länge L i und t i ein. Die Abschnitte teilen wir uns in der Regel so ein, dass wir immer eine konstante Profildicke t i haben. Was heißt das jetzt für unseren Querschnitt? Wir haben insgesamt vier Abschnitte: zwei horizontale Abschnitte mit Länge b und Dicke zwei t und zwei Abschnitte mit Länge h und Dicke t. Jetzt laufen wir die Kontur einfach im Kreis ab, beginnend in der unteren rechten Ecke. Das heißt das Ringintegral ergibt sich zu:

Betrachten wir jetzt wieder Stahl mit einem Schubmodul von 80.000 Megapascal unter der gleichen Last wie der Kreisquerschnitt. Damit können wir die Verdrillung auch vergleichen. Wenn wir die ersten Bredtsche Formel einsetzen, erhalten wir eine Verdrillung von:

Die Fläche berechnet sich diesmal mit h mal b. Also wieder der gesamten eingeschlossenen Fläche. Setzen wir die Werte ein, erhalten wir:


Dieser Wert beschreibt den Widerstand gegen Verdrillung. Du erkennst sicher, dass wir eine deutlich größere Verdrillung als beim Kreisquerschnitt erhalten.

