Balkentheorie
Du siehst in der Festigkeitslehre vor lauter Balken den Wald nicht mehr? Kein Problem! In diesem Video erklären wird dir die wichtigsten Annahmen der Balkentheorie
Inhaltsübersicht
Euler-Bernoulli und Timoshenko-Balken
Die Balkentheorie beschreibt das mechanische Verhalten von Balken bei Belastung, vor allem bei der Biegung. Sie kann nicht nur auf einzelne Balken, sondern auch auf Bauteile, die aus mehreren Balken besteht, angewendet werden. Wichtige Größen in der Balkentheorie sind die Biegelinie
, das Biegemoment sowie Längs- und Querverformungen.
Einen Balken zu beschreiben kann sich dabei schwieriger gestalten als zunächst vielleicht vermutet. Verschiedene Wissenschaftler haben sich bereits daran versucht und Modelle zur Berechnung entwickelt. Wir werden uns die wichtigsten ansehen: Den Euler-Bernoulli und der Timoshenko-Balken.
Doch zuerst schauen wir uns einige Grundlagen an. Ein Balken ist immer biegesteif. Das heißt, er ist steif gegen eine Verbiegung von außen. Wird der Balken nur entlang seiner Längsachse belastet, wird er als Stab bezeichnet. Für die Berechnung der Belastungsgrößen eines Balkens gibt es drei Theorien, die angewandt werden.
Theorie erster Ordnung
Bei der Theorie erster Ordnung werden die Kräfte und Momente am unverformten Balken ermittelt. Dafür berechnen wir zunächst das Biegemoment M aus der Kraft und dem Abstand  .
.

Mithilfe der Biegesteifigkeit können wir außerdem bestimmen, wie groß das Biegemoment im Verhältnis zur Krümmung ist. Für homogene Querschnitte wird die Biegesteifigkeit als Produkt aus dem Elastizitätsmodus des Materials und dem Flächenträgheitsmoment I bestimmt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Theorie zweiter Ordnung
Bei der Theorie zweiter Ordnung werden die Kräfte und die Momentelemente am verformten Balken berechnet. Hier kommt ein lineares mathematisches Modell zum Einsatz. Bei der Theorie zweiter Ordnung müssen wir noch die Vorverformung f berücksichtigen. Es ergibt sich folgendes Moment.

Theorie dritter Ordnung
Bei der Theorie dritter Ordnung werden Kräfte und Momente mit Hilfe eines nichtlinearen mathematischen Modells am verformten Balken berechnet. Das Ganze können wir uns beispielsweise an dieser Balkenkonstruktion ansehen:
Hierbei wird zusätzlich der Winkel der Theorie dritter Ordnung berücksichtigt und wir stellen wieder die Momentgleichung auf:

Euler-Bernoulli-Balken
Sehr schön! Kommen wir zu unserem ersten Balken: Der Euler-Bernoulli-Balken. Ist bei diesem der Querschnitt im unbelasteten Zustand senkrecht zur Nulllinie angeordnet, bleibt dieser auch bei der Belastung eben. Folgendes wird für den Euler-Bernoulli Balken angenommen
- Seine Länge ist viel größer als der Querschnitt
- Der Schwerpunkt des Querschnitts unterliegt nur einer Verschiebung
- Die Verformungen, die auftreten, sind gering
- Es gibt keine Vorwölbungen
- Nur ein eindimensionaler Spannungszustand tritt auf
Sehen wir uns den Balken doch einmal an:
Die Verzerrung ist dabei  und die Verdrehung
und die Verdrehung 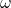 ´. k ist ein Korrekturfaktor für den Fall einer ungleichen Verteilung der Schubspannung im Balken. Mit Hilfe des Gleitmoduls G und der Fläche A können wir nun die Schubsteifigkeit Q berechnen.
´. k ist ein Korrekturfaktor für den Fall einer ungleichen Verteilung der Schubspannung im Balken. Mit Hilfe des Gleitmoduls G und der Fläche A können wir nun die Schubsteifigkeit Q berechnen.

Das Moment M hängt von dem Elastizitätsmodul E, dem Flächenträgheitsmoment i und der Verzerrung  ab. Es gilt:
ab. Es gilt:

Timoshenko-Balken
Der Timoshenko Balken ist ein Spezialfall des Euler-Bernoulli Balkens für besonders hohe Schubfestigkeit. Für diesen gilt zusätzlich
6. Die Querschnittsnormale ist nicht unbedingt parallel zur Tangente der Biegelinie
Der Timoshenko Balken wird in der erweiterten Balkentheorie genutzt. Dabei wird die Schubverformung der Querschnittsebene berücksichtig. Das sieht dann folgendermaßen aus. Die Gleichungen für den Timoshenko Balken lauten analog zu den vorherigen Gleichungen:
Perfekt! Nun kennst du die beiden wichtigsten Balkenarten in der Balkentheorie und kannst ihre Größen bestimmen.


