Torsionsspannung
In diesem Beitrag zeigen wir dir wie du Torsionsspannung bei dünnwandigen Querschnitten berechnen kannst. Außerdem erklären wir das Torsionsmoment.
Du möchtest das alles in einem Video erklärt bekommt, anstatt langen Text zu lesen? Dann schau doch hier mal rein.
Inhaltsübersicht
Torsionsspannung einfach erklärt
Die Torsion beschreibt eine Verdrehung eines Körpers. Diese Verdrehung wird durch ein Torsionsmoment verursacht und erzeugt innerhalb des Objekts eine Spannung, der Torsionsspannung. Dabei treten bei einer Torsion nur Schubspannungen auf.
Die Torsionsspannung  ist mathematisch definiert als:
ist mathematisch definiert als:

M ist dabei das Torsionsmoment und W das Widerstandsmoment .
Torsionsmoment
Um die Formel der Torsionsspannung genau zu erklären, zeigen wir dir kurz was es mit dem Torsionsmoment auf sich hat. Dieses ist für die Verdrillung verantwortlich. Und zwar beschreibt ein Moment in der technischen Physik eine Kraft, die auf einen Punkt oder eine Drehachse über einen Hebel wirkt. Das Torsionsmoment ist so die Kraft, die bei dem Körper die Verdrillung auslöst.
Diesen Zusammenhang in eine mathematische Formel übersetzt ergibt:

M ist das Torsionsmoment und F die Kraft, die über den Hebel, zum Beispiel einem Radius r angreift.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Torsionsspannung berechnen
Betrachten wir nun die Torsion von dünnwandigen Rohren. Du weißt ja, dass dünnwandig heißt, dass die Profildicke deutlich geringer ist als die restlichen Abmessungen. Zudem wollen wir jetzt ausschließlich die reine Torsion betrachten und gehen davon aus, dass keine weiteren Momente beziehungsweise Kräfte angreifen.
Die Profildicke muss aber nicht konstant sein. Die einzige Bedingung, die wir stellen, ist, dass wir keine Änderung in Balkenrichtung haben. Das heißt, wir lassen eine Änderung in Umfangrichtung zu. Als Laufvariable für die Umfangrichtung verwenden wir „klein u“.
Normal- und Schubspannungen
Du kannst dir sicher denken, dass bei einer Torsion keine Normalspannungen auftreten, da wir ja in keine Richtung am Balken ziehen. Dementsprechend haben wir eine reine Schubspannungsbelastung. Wenn wir aus der Schubspannung eine Kraft machen wollen, benötigen wir die Fläche. Diese ergibt sich aus der Profildicke t und der Länge dx. Damit erhalten wir:

Daraus können wir dann das Kräftegleichgewicht bilden:

Damit erkennen wir schnell, dass gilt:

Das Produkt aus Schubspannung und Profildicke wird Schubfluss genannt. Aus dem Gleichgewicht erhalten wir, dass der Schubfluss konstant sein muss!
Formeln der Torsionsspannung
Damit können wir uns dann die erste Bredt’sche Formel herleiten.
Dafür machen wir wieder eine Betrachtung am Balkenelement. Es greift also ein infinitesimales Moment d M T an. Das Moment verursacht Schubspannungen im Abstand zur x-Achse, an der das Moment angreift. Der Abstand wird mit c beschrieben. Die Fläche setzt sich in diesem Fall aus der Profildicke t und der Laufvariable d u zusammen. Damit ergibt sich:

Betrachten wir jetzt das Dreieck, das sich aus c und d u ergibt. Die Fläche können wir ganz einfach bestimmen zu:

Das setzen wir jetzt in die Formel für das Moment ein:

und integrieren. Dabei wissen wir, dass „Tau mal t“ konstant ist. Wir erhalten also:

Dies können wir umformen und so die Torsionsspannung bestimmen:

Wichtig ist hier, dass wir nicht die Fläche des Rohrs betrachten, sondern die gesamte eingeschlossene Fläche, auch wenn diese eigentlich „leer“ ist. Für ein kreisrundes Rohr wäre die Fläche:

Für ein Rohr mit dem Radius von 150 Millimetern und einer Profildicke von fünf Millimetern können wir für ein Moment von 20 Kilonewton die Schubspannung berechnen zu:
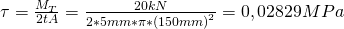
Die Aufgabe ist damit gelöst!
Super, jetzt weißt du was für Kräfte bei Torsionsspannungen auftreten und wie du sie berechnen kannst.

