Video

Quiz

Hookesche Gerade

Bei der Hookeschen Gerade denkst du an Captain Hook aus Peter Pan, in der Festigkeitslehre hast du jedoch noch nie davon gehört? In diesem Video erklären wir sie dir!

Inhaltsübersicht

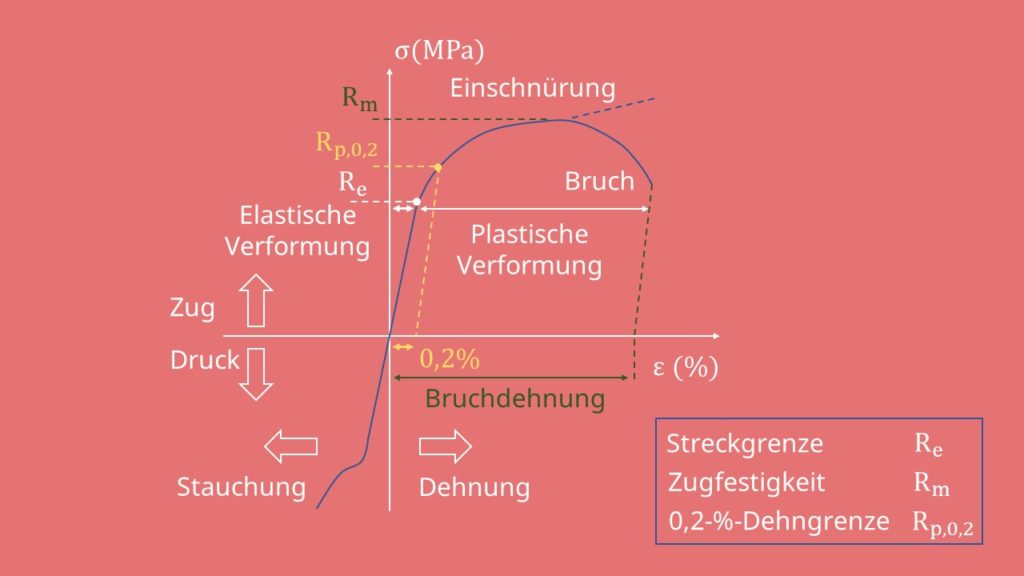
Zusammenhang zwischen Spannung und Dehnung

Die Hookesche Gerade und auch das Hookesche Gesetz beschäftigen sich mit dem Zusammenhang von Spannung und Dehnung bei Materialien unter Zug- oder Druckbelastung. Die Gerade dient der Beschreibung des linear-elastischen Verhaltens von Festkörpern wie zum Beispiel bei Metallen, Glas oder Keramik.

Hookesches Gesetz Formel

Wir betrachten hier den eindimensionalen Fall. Eindimensional heißt, dass der Werkstoff nur in eine Richtung gedehnt wird. Wir wählen hier die x-Richtung. Erinnerst du dich an unser Video zum Zugversuch? Zu Beginn haben wir hier den linearen elastischen Bereich, der auch als „Hookesche Gerade“ bezeichnet wird.

Hookesche Gerade, Hookesches Gesetz — Der linear elastische Bereich ist die Hookesche Gerade

Diese wird durch das Hookesche Gesetz beschrieben. Die Formel dafür Gesetz lautet:

$\sigma_x=\varepsilon_x*E$

Epsilon beschreibt die Dehnung des Werkstoffs in x-Richtung und kann auch durch folgende Gleichung beschrieben werden:

$\varepsilon_x$ = $\frac{\Delta\l}{l_0}$

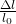
Groß E steht im Hookeschen Gesetz für den Elastizitätsmodul, auch Young´s Modulu, E-Modul, Zugmodul oder Dehnungsmodul genannt und ist ein Maß für die sogenannte Steifigkeit des Werkstoffes. Dieser wird in Kraft pro Fläche angegeben, also beispielsweise in Megapascal (MPa= $\frac{N}{{mm}^2}$ ) und entspricht der Steigung der Spannungs-Dehnungskurve, also $\sigma_x$ durch $\varepsilon_x$ .

$E=\frac{\sigma_x}{\varepsilon_x}$

In der Regel wird er aus einem zerstörenden Versuch bestimmt. Damit haben wir schon fast alle Bestandteile des Hookeschen Gesetzes kennengelernt, nun fehlt nur noch die Spannung Sigma. Sie berechnet sich aus der aufgebrachten Zug-Kraft pro Fläche in x- Richtung.

$\sigma_x=\frac{F_x}{A}$

Wirkung einer Kraft auf einen elastischen Körper

Das Hookesche Gesetz beschreibt also die Wirkung einer Kraft auf einen elastischen Festkörper, wie zum Beispiel Federn oder Gummibänder. Elastische Körper gehen nach einer Belastung durch Zug oder Druck in ihre ursprüngliche Form zurück. Überschreitet die Spannung die sogenannte Streckgrenze R_e verlässt der Werkstoff den rein elastischen Bereich und die Formel des Hookeschen Gesetz ist nicht mehr gültig.

Anwendung des Hookeschen Gesetzes – Beispiel

Schauen wir uns dazu doch einmal ein konkretes Beispiel an.

Hookesche Gerade, Hookesches Gesetz — Beispielaufgabe

Nehmen wir an, wir haben einen Stahlträger der Länge l und der Höhe h, der von einem Stahlseil in der Höhe a über dem Balken gehalten wird. Nun wollen wir mithilfe des hookeschen Gesetzes die prozentuale Dehnung und die Längenänderung des Seiles berechnen. Die Spannung $\sigma$ sowie der Elastizitätsmodul E, die Höhe a der Einspannung, die Länge l des Trägers und der Höhenunterschied h sind uns gegeben.

$\sigma=190\ MPa$

$E=230\ GPa$

a=4m

$h=0,5\ m$

l=20m

Mithilfe des Hookeschen Gesetzes berechnen wir zunächst die Dehnung. Dazu stellen wir die Gleichung zunächst nach $\varepsilon$ um. Es ergibt sich:

$\varepsilon=\frac{\sigma}{E} =\frac{190\ MPa}{230\ GPa} = 0,083%$

Wir setzen unsere gegebenen Werte ein und erhalten eine prozentuale Dehnung von 0,083%. Für die Längenänderung verwenden wir unsere zweite Formel.

$\varepsilon_x$ = $\frac{\Delta\l}{l_0}$

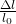
Wir berechnen die Länge des Stahlseiles zu Beginn mit dem Satz des Pythagoras und erhalten:

$\sqrt{{(a-h)}^2+l^2\ }\ = \sqrt{{(4m-0,5m)}^2+{20m}^2} = 20,3 m$

Nachdem wir die Länge und die Dehnung eingesetzt haben, ergibt sich eine Längenänderung von 1,68 m.

$\Delta\l$ = $l_0*\varepsilon = 20,3 m * 0,083 = 1,6849 m = 1,68 m$

Sehr schön! Du weißt jetzt was die Hookesche Gerade ist und kennst die einzelnen Komponenten des Hookeschen Gesetzes.

zur Videoseite: Hookesche Gerade

Beliebte Inhalte aus dem Bereich Festigkeitslehre

Intro Festigkeitslehre Dehnungen

Elastizitätsmodul

Querkontraktionszahl / Poissonzahl

Zug- und Torsionsversuch

Hookesche Gerade

Wärmeausdehnungskoeffizient

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .