Standorttheorie Weber – kontinuierliche Standortplanung
Die kontinuierliche Standortplanung nach der Standorttheorie Weber ist ein wichtiges Konzept im Supply Chain Management. Mithilfe dieses Modells kannst du den kostenminimalen Standort eines Lagers oder einer Produktionsstätte bestimmen. Wir erklären dir das Steiner-Weber-Modell Schritt für Schritt anhand eines einfachen Beispiels.
Das Thema kannst du noch schneller verstehen, indem du ganz einfach unser Video dazu anschaust.
Inhaltsübersicht
Kontinuierliche Standortplanung
Wir befinden uns mit der Standortplanung im Bereich der Distribution in der Supply Chain. Mit Hilfe der kontinuierlichen Standortplanung kannst du relativ einfach herausfinden, wo auf der Landkarte du deine Produktionsstätten für Elektroroller am besten platzierst. Bei der kontinierlichen Standortplanung gibt es unendlich viele mögliche Standorte die durch Verschiebung des Standortes erreicht werden können. In dieser Hinsicht unterscheidet sich diese Art der Standortplanung von der diskreten Standortplanung , welche nur eine begrenze Anzahl potenzieller Standorte bei der Planung zulässt.
Standorttheorie nach Weber
Das bekannteste Beispiel der kontinuierlichen Standortplanung ist die Standorttheorie Weber bzw. das Steiner-Weber-Modell. Mithilfe dieses Modells kann man den kostenminimalen Standort eines Lagers oder einer Produktionsstätte bestimmen. Im Rahmen des Steiner-Weber-Modells werden, im Gegensatz zur diskreten Standortplanung, keine potentiellen Standorte vorgegeben. Um dennoch zu einem Ziel zu gelangen, wird üblicherweise eine Karte mit einem Koordinatensystem angenommen. Der Vorteil dabei ist, dass der optimale Standort auf den Millimeter genau bestimmt werden kann – der Nachteil ist allerdings, dass nicht sichergestellt werden kann, ob an diesem Punkt überhaupt gebaut werden kann, oder ob es sich beispielsweise um ein Naturschutzgebiet handelt.
Standorttheorie Weber Beispiel
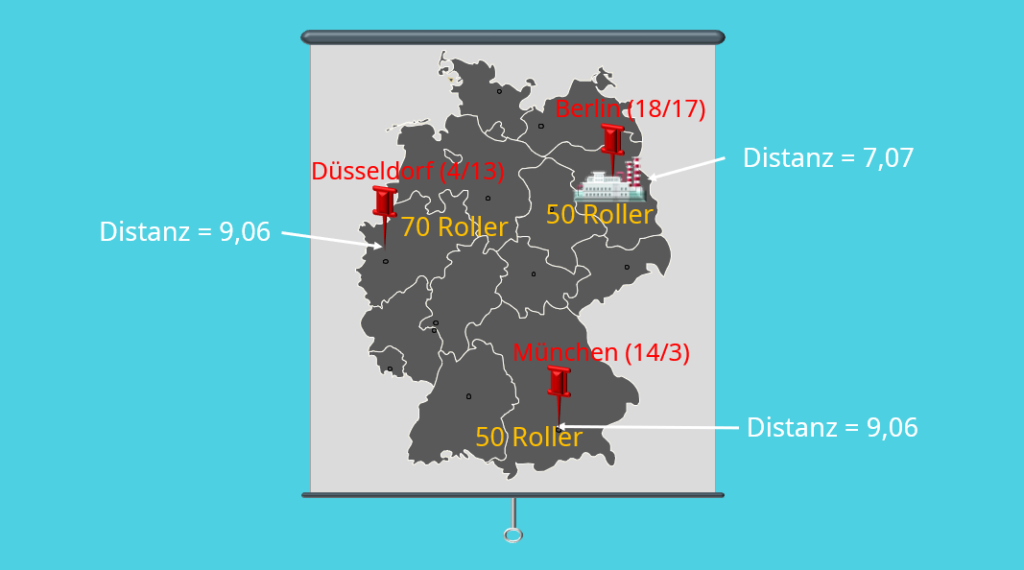
Um die Standorttheorie von Alfred Weber besser verstehen zu können, schauen wir uns das Problem an einem einfachen Beispiel an. Dazu betrachten wir zunächst eine Deutschlandkarte mit einigen bestehenden Standorten. Nehmen wir an, du hast einen Standort in München mit den Koordinaten (14/3), einen in Berlin (18/17) und einen in Düsseldorf (4/13). Ziel ist es nun, die optimalen Koordinaten (x*, y*) deines neuen Zentrallagers herauszufinden. Zentraler Bestandteil des Steiner-Weber-Modells ist also, dass die Transportkosten möglichst gering sein sollen.
Für die Berechnung der optimalen Koordinaten musst du neben den Koordinaten deiner bisherigen Standorte auch ihre Bedarfe 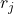 an Rollern kennen. Diese hängen davon ab, wie hoch die Nachfrage der Kunden in den jeweiligen Vertriebsregionen ist. Du weißt, dass München und Berlin täglich jeweils
an Rollern kennen. Diese hängen davon ab, wie hoch die Nachfrage der Kunden in den jeweiligen Vertriebsregionen ist. Du weißt, dass München und Berlin täglich jeweils 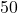 und Düsseldorf
und Düsseldorf 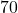 Roller benötigen. Da du aber alle Roller, also insgesamt
Roller benötigen. Da du aber alle Roller, also insgesamt 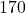 Stück in Berlin produzierst, darfst du den Bedarf für Berlin nicht miteinbeziehen. Denn diese befinden sich ja bereits in Berlin. Ziehst du die
Stück in Berlin produzierst, darfst du den Bedarf für Berlin nicht miteinbeziehen. Denn diese befinden sich ja bereits in Berlin. Ziehst du die 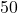 von den
von den 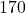 Rollern ab erhältst du
Rollern ab erhältst du 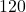 Roller, die von Berlin zum neuen Zentrallager geliefert werden müssen. Du rechnest also mit diesem Wert.
Roller, die von Berlin zum neuen Zentrallager geliefert werden müssen. Du rechnest also mit diesem Wert.
Berechnung der optimalen Koordinaten nach der Standorttheorie Weber
Jetzt können wir uns die Berechnung von 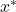 und
und 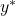 in der Standorttheorie Weber anschauen. Da es ja um möglichst geringe Transportkosten geht, müssen wir uns erst einmal anschauen, wie deine Kostenfunktion bei der kontinuierlichen Standortplanung im Steiner-Weber-Modell aussieht.
in der Standorttheorie Weber anschauen. Da es ja um möglichst geringe Transportkosten geht, müssen wir uns erst einmal anschauen, wie deine Kostenfunktion bei der kontinuierlichen Standortplanung im Steiner-Weber-Modell aussieht.
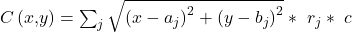
Sie setzt sich aus der Luftlinienentfernung zwischen dem neuen Lager und deinem Standort, dem Bedarf des Standorts und den Kosten pro Mengen- und Längeneinheit zusammen. Die Gesamtkosten im Steiner Weber Modell erhältst du, wenn du die Kosten für alle Standorte berechnest und summierst.
Standorttheorie Weber: Berechnung der minimalen Transportkosten mithilfe der euklidischen Distanz
Diese Formel allein bringt dir aber nichts, wenn du die  – und
– und 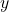 -Werte im Steiner Weber Modell herausfinden willst, bei denen die Transportkosten minimal sind. In der Standorttheorie Weber müssen wir das Miehle Verfahren, ein iteratives Verfahren, anwenden und die Kostenfunktion nacheinander nach
-Werte im Steiner Weber Modell herausfinden willst, bei denen die Transportkosten minimal sind. In der Standorttheorie Weber müssen wir das Miehle Verfahren, ein iteratives Verfahren, anwenden und die Kostenfunktion nacheinander nach  und
und 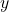 ableiten.
ableiten.
Nehmen wir an, die Kosten pro Mengen- und Längeneinheit im Steiner Weber Modell betragen 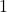 . Dann erhalten wir für
. Dann erhalten wir für  mithilfe der Formel für die euklidische Distanz:
mithilfe der Formel für die euklidische Distanz:
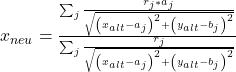
Und für 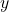 :
:
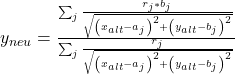
Auf den ersten Blick sehen die Formeln sehr kompliziert aus. Aber eigentlich ist das Vorgehen ganz einfach. Die Koordinaten (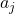 ,
, 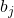 ) und die Bedarfe
) und die Bedarfe 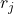 deiner Standorte kennst du bereits. Die Startwerte
deiner Standorte kennst du bereits. Die Startwerte 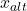 und
und 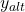 sind dir in der Standorttheorie Weber normalerweise gegeben. Wenn nicht, dann kannst du sie beliebig auswählen. Sagen wir z.B.
sind dir in der Standorttheorie Weber normalerweise gegeben. Wenn nicht, dann kannst du sie beliebig auswählen. Sagen wir z.B.  ist
ist 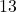 und
und 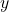 ist
ist 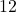 . Jetzt können wir
. Jetzt können wir 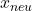 und
und 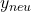 Schritt für Schritt ausrechnen.
Schritt für Schritt ausrechnen.
Am besten berechnest du als erstes die Entfernungen 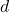 der bisherigen Standorte zu den gewählten Koordinaten. Das sieht dann so aus:
der bisherigen Standorte zu den gewählten Koordinaten. Das sieht dann so aus:
Du kommst also für München auf eine Distanz von 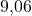 , für Berlin von
, für Berlin von 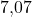 und für Düsseldorf auf eine Distanz von
und für Düsseldorf auf eine Distanz von 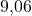 . Als nächstes schauen wir uns den gesamten Zähler im Miehle Verfahren an und setzen unsere Werte ein. Für
. Als nächstes schauen wir uns den gesamten Zähler im Miehle Verfahren an und setzen unsere Werte ein. Für 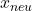 ergibt sich dann ein Wert von
ergibt sich dann ein Wert von 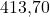 und für
und für 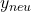
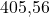 . Jetzt fehlt nur noch der Nenner. Der ist für
. Jetzt fehlt nur noch der Nenner. Der ist für 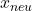 und
und 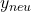 gleich. Wir erhalten dann für beide einen Wert von
gleich. Wir erhalten dann für beide einen Wert von 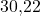 .
.
Ergebnisse der Standorttheorie Weber
So jetzt musst du deine Ergebnisse nur noch zusammensetzen. Für  und
und 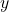 ergeben sich im Steiner-Weber-Modell folgende neue Werte:
ergeben sich im Steiner-Weber-Modell folgende neue Werte:
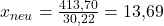 und
und 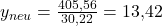
Jetzt hast du die 1. Iteration des Miehle-Verfahrens durchgeführt. Aber woran siehst du jetzt, dass dein Ergebnis wirklich der optimale Standort für dein neues Lager ist? Dazu gibt es im Steiner Weber Modell den Wert Ɛ, mit dem du dein Ergebnis prüfen kannst. Dieser ist dir immer angegeben. Trifft die folgende Bedingung zu, dann hast du die optimale Lösung der Standorttheorie Weber gefunden. Für Epsilon ist uns der Wert 2,49 gegeben. Setzten wir unsere Werte ein, dann erhalten wir für das Steiner Weber Modell:
Damit stimmen unsere Werte überein und wir wissen, dass wir schon die richtigen Standortkoordinaten herausgefunden haben. Wäre unser Wert aber zum Beispiel 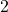 , trifft die Bedingung nicht zu und du musst noch eine zweite Iteration mit deinen neuen
, trifft die Bedingung nicht zu und du musst noch eine zweite Iteration mit deinen neuen  – und
– und 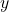 -Werten durchführen. Wir nähern uns so also immer weiter an die optimalen Koordinaten deines neuen Standorts an. Nach jeder Iteration im Steiner-Weber-Modell prüfst du, ob du die optimale Lösung gefunden hast.
-Werten durchführen. Wir nähern uns so also immer weiter an die optimalen Koordinaten deines neuen Standorts an. Nach jeder Iteration im Steiner-Weber-Modell prüfst du, ob du die optimale Lösung gefunden hast.
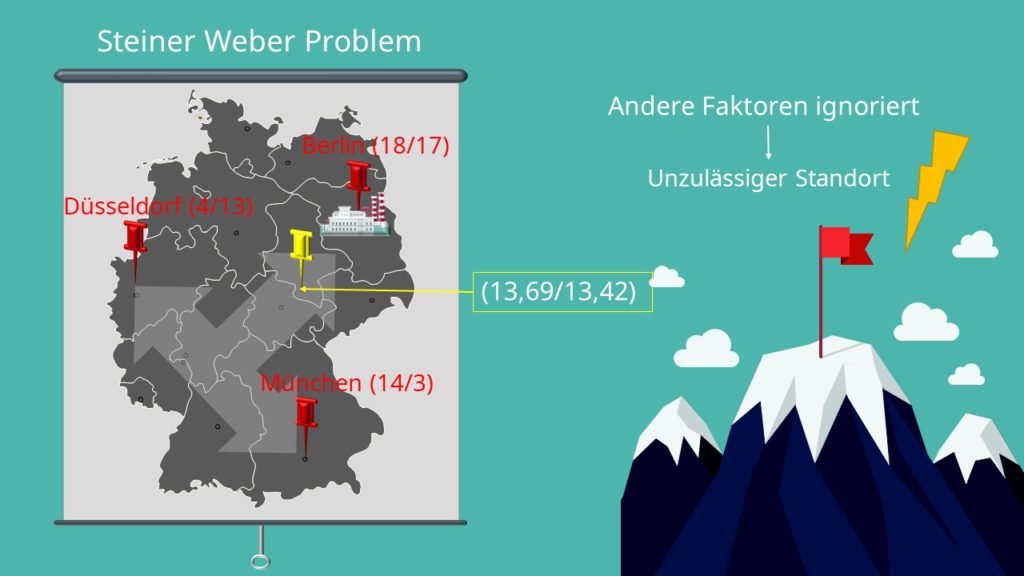
Wo sollten wir unser Lager nun optimaler Weise errichten, wenn wir davon ausgehen, dass die Genauigkeit 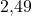 beträgt und wir die beste Lösung gefunden haben? Schauen wir uns nochmal die Deutschlandkarte an. Tragen wir die Koordinaten (13,69/13,42) ein, landen wir auf einem Punkt, der in einem Naturpark zwischen Erfurt und Halle liegt.
beträgt und wir die beste Lösung gefunden haben? Schauen wir uns nochmal die Deutschlandkarte an. Tragen wir die Koordinaten (13,69/13,42) ein, landen wir auf einem Punkt, der in einem Naturpark zwischen Erfurt und Halle liegt.
Standorttheorie Weber Probleme
Du siehst, dass in der Standorttheorie Weber nur auf räumliche Entfernungen zwischen den Standorten und ihrem Warenbedarf geachtet wird und weitere Faktoren komplett ignoriert werden. So kann es im Steiner-Weber-Modell passieren, dass du am Ende auf einen unzulässigen Standort kommst. Das ist eine große Schwäche der Standorttheorie Weber und ein wesentlicher Unterschied zur diskreten Standortplanung bzw. zum Nutzwertanalyse Beispiel – Socring Modell.