Du möchtest wissen, was das Massenwirkungsgesetz besagt, welche Größen das chemische Gleichgewicht beeinflussen und wie sich die Gleichgewichtskonstante berechnen lässt? Dann bist du hier genau richtig.
Wenn du lieber mit visuellen Methoden lernen möchtest, empfehlen wir dir unser Video zum Massenwirkungsgesetz anzusehen.
Massenwirkungsgesetz einfach erklärt
Was genau sagt uns das Massenwirkungsgesetz (kurz: „MWG„)?
Bei derartigen Reaktionen entsteht ein dynamisches Gleichgewicht in dem die Hin- und Rückreaktionen gleich schnell ablaufen.
Massenwirkungsgesetz Formel
Reagieren zwei oder mehrere Stoffe, bei konstanten äußeren Bedingungen (z.B. Temperatur) reversibel miteinander, stellt sich nach einer gewissen Zeit ein Gleichgewicht ein. Dabei kommt die Reaktion nicht zum Stillstand, weshalb man auch von einem dynamischen Gleichgewicht spricht. Hin- und Rückreaktionen laufen weiterhin ab. Da diese im Gleichgewicht gleich schnell ablaufen stellt sich bei den Aktivitäten der Produkte und der Edukte ein konstanter Wert ein. Dabei wird der energetisch günstigste Zustand angestrebt, also ein Minimum der Gibbs-Energie.
Die allgemeine Formel für die Gleichgewichtskonstante lautet:
Dabei sind:
- K = Gleichgewichtskonstante der Reaktion
-
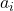= Aktivität der i-ten Sorte -
= stöchiometrischer Koeffizient der i-ten Sorte (für Edukte 
<0, für Produkte >0)
Für die Beschreibung der Gleichgewichtskonstante werden, je nach Reaktionstyp, andere Parameter anstelle der Aktivitäten verwendet. Bei Reaktionen in verdünnten Lösungen werden etwa die Stoffmengenkonzentrationen der Reaktionspartner genutzt. Da die Berechnung mit unterschiedlichen Parametern den Zahlenwert von K ändern kann, wird der Gleichgewichtskonstanten ein entsprechender Index angefügt. (z.B. 
, mit c = Konzentration)
Die Gleichgewichtskonstante selbst gibt an, ob sich das chemische Gleichgewicht einer Reaktion eher auf der Seite der Produkte (K>1) oder oder auf der Seite der Edukte (K<1) befindet.
Sie selbst ist unabhängig vom Druck, dem Einsatz eines Katalysators und den Stoffmengen der Reaktanden und beschreibt nicht, wie schnell eine Reaktion abläuft.
Aber wie kann man sich so ein chemisches Gleichgewicht in der Praxis zunutze machen? Dafür betrachten wir einmal das Prinzip von Le Chatelier, welches besagt:
Wird auf ein System, das sich im chemischen Gleichgewicht befindet, ein Zwang durch Änderung der äußeren Bedingungen ausgeübt, so entsteht ein neues Gleichgewicht, welches dem äußeren Zwang ausweicht.
- So kann etwa einerseits, durch fortlaufende Entnahme eines Produktes aus dem System, dasselbe Produkt nachgebildet werden.
- Andererseits würde eine externe Wärmezufuhr eine endotherme Reaktion und eine Wärmereduktion respektive eine exotherme Reaktion begünstigen.
Massenwirkungsgesetz in der Gasphase
Zur Berechnung der Gleichgewichtskonstante werden bei Reaktionen in der Gasphase die Partialdrücke als Parameter genutzt. Die Formel hierfür lautet:
Mit:
-
= Partialdruck der i-ten Sorte
Schauen wir uns einmal die Berechnung am Beispiel der Ammoniaksynthese im Haber-Bosch-Verfahren genauer an. Die Reaktionsgleichung lautet:
Für die Gleichgewichtskonstante gilt somit:
Zwischen 
und existiert ein simpler Zusammenhang, der sich mithilfe der idealen Gasgleichung darstellen lässt. Die Gasgleichung lautet:
Daraus folgt:
Hierbei sind:
-
= Stoffmenge der i-ten Sorte - R = universelle Gaskonstante
- V = Volumen
- T = Temperatur in Kelvin
Bei der Bildung von Ammoniak ergibt sich für unsere Massenwirkungskonstante somit:
![K_p=\frac{[c(NH_3)RT]^2}{c(N_2)RT \cdot [c(H_2)RT]^3} = \frac{c^2(NH_3)}{c(N_2) \cdot c^3(H_2)} \cdot \frac {1}{(RT)^2} = K_c \cdot \frac {1}{(RT)^2}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-7b169d106f5ccfc5a6ba717f39fcb054_l3.png "Rendered by QuickLaTeX.com")
In einem Gasphasengleichgewicht kann das Massenwirkungsgesetz somit auch folgendermaßen dargestellt werden:
Die Summe der stöchiometrischen Koeffizienten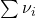 
lässt sich ganz einfach berechnen. Am Beispiel der Reaktionsgleichung zur Ammoniaksynthese ergibt sich hierbei:
Zu beachten ist noch, dass die Dimension der Massenwirkungskonstante nicht einheitlich ist. Sie hängt von der Stöchiometrie der Reaktionspartner ab.
Massenwirkungsgesetz für Flüssigkeiten
Du fragst dich nun, wie das Massenwirkungsgesetz bei verdünnten Lösungen angewendet werden kann? Die Antwort ist ganz simpel. Die Vorgehensweise ist vergleichbar mit der Gasphase. Nur musst du hier darauf achten, die Konzentrationen als Parameter zu nutzen. Wie das konkret aussieht, zeigt dir das unten stehende Beispiel.
Massenwirkungsgesetz Beispiel
Schauen wir uns zur besseren Verdeutlichung des Massenwirkungsgesetzes ein Beispiel an. Beginnen wir erneut mit der Ammoniak Synthese.
Beispiel: In einem Gefäß mit einem Volumen von 1 L werden 12 mol 
und 10 mol 
vermischt, wobei 
mit einer Konzentration von 3 
entsteht. Berechne die Gleichgewichtskonstante auf Basis der Konzentrationen.
- Die Reaktionsgleichung ist bereits weiter oben genannt:
- Das Massenwirkungsgesetz auf Basis der Konzentrationen lautet dann:
- Durch die Angabe der anfänglichen Stoffmengen und des Volumens lassen sich die anfänglichen Konzentrationen bestimmen. Diese werden benötigt um die Konzentrationen im Gleichgewichtszustand berechnen zu können, welche für eine Anwendung des Massenwirkungsgesetzes erforderlich sind:
; 
; 
- Da der Wasserstoff und der Stickstoff miteinander reagieren, ändern sich deren Konzentrationen beim Erreichen des Gleichgewichtes. Um diese Differenz berechnen zu können, müssen die Stoffmengenverhältnisse der Edukte zu den Produkten aufgestellt werden. Diese sind durch die stöchiometrischen Koeffizienten der Reaktionsgleichung bekannt:
; 
- Das Volumen von 1 L bleibt in unserem Beispiel konstant, weshalb sich die genannten Verhältnisse, durch Kürzen des Volumens, direkt auf die Konzentrationen übertragen lassen:
; 
- Anschließend können die Konzentrationen von und im Gleichgewichtszustand berechnet werden:
- Diese Werte können schließlich in das Massenwirkungsgesetz eingesetzt werden um die Gleichgewichtskonstante zu bestimmen:
Massenwirkungsgesetz Herleitung
Je höher die Aktivität der Edukte ist, desto schneller läuft eine Reaktion ab. Der genaue mathematische Zusammenhang wird mit folgender Gleichung beschrieben:
Die Reaktionsgeschwindigkeit ist also direkt proportional zur Aktivität der Reaktanden hoch ihrer jeweiligen stöchiometrischen Koeffizienten.
Da im Verlauf einer reversiblen Reaktion zunächst immer mehr Produkte durch den Verbrauch von Edukten gebildet werden, sinkt fortlaufend die Aktivität der Edukte. Gleichzeitig steigt allerdings die Aktivität der Produkte. Dies beeinflusst, wie die obige Gleichung zeigt, direkt die Geschwindigkeiten der Hin- und Rückreaktion. Sobald beide Reaktionsgeschwindigkeiten gleich hoch sind, werden genauso viele Produkte wie Edukte gebildet. Die Reaktion befindet sich im Gleichgewicht.
Eine solche Gleichgewichtsreaktion kann allgemein wie folgt dargestellt werden:
Für die Geschwindigkeiten der Hin- und Rückreaktionen folgt daraus:
; 
Hierbei ist 
die Geschwindigkeitskonstante der Hinreaktion und 
respektive die der Rückreaktion. Wie bereits genannt sind die Geschwindigkeiten der Hin- und Rückreaktion im Gleichgewichtszustand gleich hoch:
Durch weiteres Umformen ergibt sich damit die Gleichgewichtskonstante:
