Löslichkeitsprodukt
Wie du mit dem Löslichkeitsprodukt feststellen kannst, welche Menge eines Feststoffs in Wasser löslich ist, erfährst du hier!
Anschaulich dargestellt findest du alles Wichtige zum Löslichkeitsprodukt auch in unserem Video .
Inhaltsübersicht
Löslichkeitsprodukt einfach erklärt
Das Löslichkeitsprodukt, auch KL-Wert genannt, sagt dir, was bei einer gegebenen Temperatur die maximal lösliche Menge eines Salzes in Wasser ist. Dabei handelt es sich immer um folgende Reaktion, bei der die Ionen eines Salzes von Wasser gelöst werden.
AB  A+ + B–
A+ + B–
Anhand dieser Reaktion ist das Löslichkeitsprodukt auch definiert:

 =Löslichkeitsprodukt, c=Konzentration
=Löslichkeitsprodukt, c=Konzentration
Überschreitet das Produkt der beiden Konzentration der Ionen A und B das Löslichkeitsprodukt, fällt das Salz als Feststoff aus. Das Löslichkeitsprodukt gibt dir also die Sättigungskonzentration eines Salzes an.
Löslichkeitsprodukt Formel
Als ersten Schritt ist es immer wichtig, dass du verstehst, woher das Massenwirkungsgesetz kommt und was es aussagt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Löslichkeitsprodukt Herleitung über das Massenwirkungsgesetz
Das Löslichkeitsprodukt ist eine Vereinfachung des Massenwirkungsgesetzes, du kannst es daher auch leicht davon ableiten. Wenn du mehr zum Thema Massenwirkungsgesetz lernen möchtest, dann klicke doch hier .

a=Aktivität; i=Stoffindex;  =Stöchiometrie Koeffizient
=Stöchiometrie Koeffizient
Nun schau dir als nächstes eine typische Lösungsreaktion an:

z.B. 


Dann lautet das Massenwirkungsgesetz so:

oder für  :
: 
Wie immer beim Massenwirkungsgesetz, musst du auch hier darauf achten, dass die stöchiometrischen Koeffizienten berücksichtigt sind! Im nächsten Schritt kannst du die Aktivität deines Feststoffes, also  bzw.
bzw.  gleich 1 setzen. Danach ersetzt du noch die Aktivitäten durch Konzentrationen, weil dies für stark verdünnte Lösungen eine gute Näherung darstellt. Dann erhältst du die Löslichkeitskonstante:
gleich 1 setzen. Danach ersetzt du noch die Aktivitäten durch Konzentrationen, weil dies für stark verdünnte Lösungen eine gute Näherung darstellt. Dann erhältst du die Löslichkeitskonstante:

bzw. 
Molare Löslichkeit
Neben dem Löslichkeitsprodukt existiert auch noch eine etwas griffigere Definition der Löslichkeit eines Feststoffes: die molare Löslichkeit. Sie gibt dir die Löslichkeit nicht nur als Produkt zweier Ionen-Konzentrationen an, sondern liefert einen realen Wert, wie viel Mol pro Liter eines Salzes im Wasser löslich sind. Diese molare Löslichkeit leitet sich auf recht einfache Weise aus der Löslichkeitskonstante ab:


Außerdem weißt du, dass die Konzentration des Ions A das 2-fache der Salzkonzentration sein muss, da ja bei der Reaktion durch 1 mol Salz 2 mol an Ion A entstehen. Wiederum gilt für Ion B, dass dessen Konzentration das 3-fache der Salzkonzentration sein muss, da ja bei der Lösungsreaktion aus 1 mol Salz 3 mol Ion B entstehen.
c( )= 2 c(Salz)
)= 2 c(Salz)
c(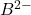 }= 3 c(Salz)
}= 3 c(Salz)
Das musst du nun in die Definition des Löslichkeitsprodukts einsetzen und erhältst dann:

c(Salz)=![Rendered by QuickLaTeX.com \sqrt[3+2]{\frac {K_l}{3^3*2^2}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c9604269611c2c663551c497c4f2598d_l3.png)
oder allgemeiner:
c(Salz)=![Rendered by QuickLaTeX.com \sqrt[n+m]{\frac {K_l}{n^n*m^m}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-80206b6a621c456ab3334a4589cc830e_l3.png)
Löslichkeitsprodukt Einheit
Vielleicht ist dir schon aufgefallen, dass die Einheiten des Löslichkeitsprodukt variieren können, je nachdem welches Salz man betrachtet. So hat zum Beispiel NaCl die folgende Einheit:
 Einheit:
Einheit: 
Das Löslichkeitsprodukt für  sieht dagegen folgendermaßen aus:
sieht dagegen folgendermaßen aus:
 Einheit:
Einheit: 
Die Einheit des Löslichkeitsprodukt richtet sich also immer nach den stöchiometrischen Koeffizienten der Ionen in der Lösung. Aufgrund dieser verschiedenen Einheiten kannst du die Löslichkeitsprodukte zweier Salze nur bei gleicher Einheit mit einander vergleichen.
Gesättigte Lösung Definition und berechnen
Die Definition einer gesättigten Lösung ist, dass die maximal mögliche Menge an Salz in der vorliegenden Flüssigkeit, meist Wasser, gelöst ist. Wenn du jedoch noch mehr Salz hinzugeben würdest, würde dieses nicht mehr gelöst werden, bzw. dieselbe Menge würde als Feststoff ausfallen.
Die Sättigungskonzentration kannst du leicht über das Sättigungsprodukt herausfinden. Nimm an, du hättest zum Beispiel folgende Reaktionsgleichung von AgCl:

Dann brauchst du noch das Löslichkeitsprodukt von AgCl:

Da die Konzentration der Silber-Ionen gleich der Konzentration der Chlorid Ionen sein muss, kannst du auch schreiben:

Nun musst du nur noch die Wurzel ziehen und erhältst die Sättigungskonzentration:

Löslichkeitsprodukt Bariumsulfat
Als erstes Beispiel kannst du dir das Bariumsulfat ( ) anschauen. Du möchtest herausfinden, wie viel Gramm Bariumsulfat in 1l Wasser löslich ist und was die maximalen Konzentrationen der Ionen in Lösung sind. Um das herauszufinden, stellst du erst die Reaktionsgleichung auf:
) anschauen. Du möchtest herausfinden, wie viel Gramm Bariumsulfat in 1l Wasser löslich ist und was die maximalen Konzentrationen der Ionen in Lösung sind. Um das herauszufinden, stellst du erst die Reaktionsgleichung auf:

Demnach müsste dein Löslichkeitsprodukt folgendermaßen aussehen:

Das Löslichkeitsprodukt ist eine Konstante und du kannst sie leicht nachschlagen. Für 25ºC beträgt es:
 = 10-10 mol2/l2
= 10-10 mol2/l2
Da die Konzentration von Barium-Ionen genauso groß sein muss wie die der Sulfat-Ionen, kannst du auch schreiben:

Daher kannst du durch einfaches Wurzelziehen schon die maximalen Konzentrationen der Ionen in Lösung herausfinden:

Nun brauchst du noch das maximal lösliche Gewicht an Salz, dafür verwendest du die molare Löslichkeit, die besonders einfach ist, da es nur 1 als stöchiometrische Koefizienten gibt:

Wenn du die molare Löslichkeit kennst, brauchst du sie nur noch mit der molaren Masse multiplizieren, um zu wissen wie viel Gramm pro Liter löslich sind:
 = L*M
= L*M
m=Massenlöslichkeit; L=molare Löslichkeit; M=Molare Masse

Löslichkeitsprodukt Tabelle
Zum Abschluss findest du hier noch die Löslichkeitsprodukte einiger, gängiger Salze, wie von AgCl oder Calciumsulfat, in einer Tabelle zusammengefasst:
| Salz | Löslichkeitsprodukt |
| AgCl | 2*10-10 mol2/l2 |
| Ag2S | 6*10-51 mol3/l3 |
| CaF2 | 4*10-11 mol3/l3 |
| BaSO4 | 10-10 mol2/l2 |
| CaCO3 | 5*10-9 mol2/l2 |
| Mg(OH)2 | 10-11 mol3/l3 |
| Fe(OH)2 | 10-15 mol2/l2 |
| CaSO4 | 2*10-5 mol2/l2 |
| HgS | 10-54 mol2/l2 |
