Arrhenius Gleichung
Wozu dient die Arrhenius Gleichung und wie lässt sich daraus die Aktivierungsenergie berechnen? Das erklären wir dir in dem folgenden Beitrag. Um das Thema noch schneller zu verstehen, kannst du dir gerne unser Video dazu anschauen!
Inhaltsübersicht
Arrhenius Gleichung einfach erklärt
Die Arrhenius Gleichung (auch Arrhenius Gesetz oder Arrheniusgleichung) beschreibt die Abhängigkeit der Geschwindigkeitskonstanten einer Reaktion  von der Temperatur
von der Temperatur  . Die Geschwindigkeitskonstante ist ein Maß für die Geschwindigkeit einer Reaktion. Dabei ist die Abhängigkeit in einem exponentiellen Zusammenhang gegeben.
. Die Geschwindigkeitskonstante ist ein Maß für die Geschwindigkeit einer Reaktion. Dabei ist die Abhängigkeit in einem exponentiellen Zusammenhang gegeben.

Arrhenius Gleichung und Reaktionskinetik
Die Arrhenius Gleichung setzt sich aus der Geschwindigkeitskonstanten der Reaktion  in
in  , der Temperatur
, der Temperatur  in
in 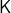 , der idealen Gaskonstanten
, der idealen Gaskonstanten
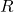 in
in  , dem Arrhenius-Vorfaktor
, dem Arrhenius-Vorfaktor  in
in  und der Aktivierungsenergie
und der Aktivierungsenergie
 in
in  zusammen. Der Arrhenius-Vorfaktor berücksichtigt unter anderem die geometrische Ausrichtung von den reagierenden Molekülen zueinander und ist reaktionsspezifisch.
zusammen. Der Arrhenius-Vorfaktor berücksichtigt unter anderem die geometrische Ausrichtung von den reagierenden Molekülen zueinander und ist reaktionsspezifisch.

Die Auftragung von  gegen
gegen  ergibt eine exponentiell verlaufende Kurve. Wir haben den folgenden Zusammenhang graphisch für dich dargestellt.
ergibt eine exponentiell verlaufende Kurve. Wir haben den folgenden Zusammenhang graphisch für dich dargestellt.
Aus der Arrhenius-Gleichung ist die dir vielleicht schon bekannte RGT-Regel (auch Reaktionsgeschwindigkeit-Temperaturregel) abzuleiten. Hier kannst du dich nochmal über die RGT-Regel
informieren. Diese besagt, dass eine Temperaturerhöhung von  mit einer Verdopplung bis Verdreifachung der Geschwindigkeitskonstante einhergeht.
mit einer Verdopplung bis Verdreifachung der Geschwindigkeitskonstante einhergeht.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Arrhenius Zahl
Der Exponent  wird auch oft als
wird auch oft als  zusammengefasst. Somit wird die Arrhenius Gleichung auch folgendermaßen dargestellt. Dabei bezeichnest du
zusammengefasst. Somit wird die Arrhenius Gleichung auch folgendermaßen dargestellt. Dabei bezeichnest du  als Arrhenius Zahl.
als Arrhenius Zahl.

Arrhenius Gleichung Aktivierungsenergie
Du kannst aus der Arrhenius Gleichung graphisch die Aktivierungsenergie
und den Arrhenius-Vorfaktor einer Reaktion bestimmen. Dazu benötigst du lediglich die logarithmierte Form der Arrhenius Gleichung. Du erhälst eine lineare Gleichung in der Form  .
.

Im Arrhenius Diagramm wird  gegen
gegen  , also die reziproke Temperatur aufgetragen. Durch die experimentelle Bestimmung von Werten für
, also die reziproke Temperatur aufgetragen. Durch die experimentelle Bestimmung von Werten für  sowie
sowie  wird nun aus der Steigung die Aktivierungsenergie
wird nun aus der Steigung die Aktivierungsenergie  einer Reaktion bestimmt. Aus dem y-Achsenabschnitt bestimmst du den Arrhenius-Vorfaktor. Unten haben wir beispielhaft ein Arrhenius Diagramm für dich dargestellt. Aus dem Graphen kannst du ganz einfach den y-Achsenabschnitt
einer Reaktion bestimmt. Aus dem y-Achsenabschnitt bestimmst du den Arrhenius-Vorfaktor. Unten haben wir beispielhaft ein Arrhenius Diagramm für dich dargestellt. Aus dem Graphen kannst du ganz einfach den y-Achsenabschnitt  sowie die Steigung
sowie die Steigung  entnehmen.
entnehmen.
Auch aus nur zwei Geschwindigkeitskonstanten  und
und  und zwei Temperaturen
und zwei Temperaturen  und
und  kannst du die Aktivierungsenergie bestimmen.
kannst du die Aktivierungsenergie bestimmen.

Arrhenius Gleichung Beispiel
Betrachten wir nun zusammen ein konkretes Anwendungsbeispiel! Wir betrachten: Den Zerfall von Distickstoffpentoxid in Stickstoffdioxid und Sauerstoff.
2 N2O5 → 4 NO2 + O2
Du hast Werte für  sowie
sowie  experimentell ermittelt und anschließend das Arrhenius Diagramm für den Zerfall von N2O5 erstellt und eine lineare Regression durchgeführt.
experimentell ermittelt und anschließend das Arrhenius Diagramm für den Zerfall von N2O5 erstellt und eine lineare Regression durchgeführt.
Die Steigung  beträgt
beträgt  und der y-Achsenabschnitt
und der y-Achsenabschnitt  beträgt 31,1. Beide Gleichungen kannst du nun nach den gesuchten Größen
beträgt 31,1. Beide Gleichungen kannst du nun nach den gesuchten Größen  sowie
sowie  umstellen.
umstellen.


Somit beträgt die Aktivierungsenergie, die für die Einleitung des Zerfalls von N2O5 benötigt wird,  . Der Arrhenius-Vorfaktor ist
. Der Arrhenius-Vorfaktor ist  .
.


