Carnot-Wirkungsgrad
Du willst endlich wissen was der Carnot-Wirkungsgrad eigentlich ist? Dann bist du hier genau richtig, denn damit beschäftigen wir uns in diesem Artikel
Inhaltsübersicht
Massenbilanz und Massenstrom
Ein Wirkungsgrad beschreibt das Verhältnis der Leistung des realen Prozesses zu der des idealen Prozesses. Der Carnot-Wirkungsgrad, auch Carnot-Faktor genannt, beschreibt den Wirkungsgrad der Umwandlung von Wärmeenergie in mechanische oder elektrische Energie. Man nennt dies auch einen Wärmekraftprozess. Aber was ist jetzt ein solcher Wärmekraftprozess?
Beispiel Motorkolben
Stellen wir uns zunächst einen Kolben im Auto vor. Nun führen wir dem Kolben das Luft-Kraftstoffgemisch zu, wodurch eine Verbrennung im Kolben stattfindet. Bei der Verbrennung entsteht Wärme und folglich steigt der Druck. Wir erzeugen also durch Wärme eine größere Kraft.
Wir definieren den Carnot-Wirkungsgrad
jetzt als:
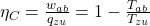
Was bedeutet das nun?
Wenn wir die Formel genauer betrachten erkennen wir:
Je kleiner der Quotient aus der Ablufttemperatur 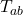 und der Zulufttemperatur
und der Zulufttemperatur 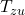 , desto größer der Wirkungsgrad.
, desto größer der Wirkungsgrad.
Für den Kolben heißt das: Führen wir Wärme mit einer Temperatur von 300 Grad Celsius zu und mit 250 Grad Celsius ab, erhalten wir einen Wirkungsgrad von:
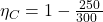
Umrechnung Grad Celsius in Kelvin
Leider ist diese Rechnung aber so noch nicht ganz richtig, weil wir immer mit der absoluten Temperatur und damit in Grad Kelvin rechnen müssen. Für die Umrechnung in Grad Kelvin musst du einfach 273,15 K zu der Temperatur in Celsius addieren. Das Ganze sieht dann so aus:
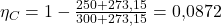
Um den Wirkungsgrad zu maximieren, gilt es also die Wärme bei möglichst hoher Temperatur zuzuführen und bei möglichst niedriger Temperatur abzuführen und damit möglichst viel Energie zu nutzen.
Um dies zu veranschaulichen, nehmen wir nun an, die Temperatur wird mit nur noch 100 Grad abgeführt. Dies wirkt sich natürlich auch auf den Wirkungsgrad aus. Wir erhalten:
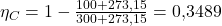
Der Wirkungsgrad hat sich gegenüber dem vorherigen Beispiel also erheblich verbessert und beträgt nun 34,89%.
So weit so gut! Nun weißt du wie man den Carnot-Wirkungsgrad für Wärmekraftprozesse bestimmt. In den folgenden Videos werden wir uns noch weitere Wirkungsgrade anschauen.
