Lagebeziehungen von Geraden
Du möchtest wissen, welche Lagenbeziehungen von Geraden möglich sind? Hier und im Video erklären wir dir alles Wichtige dazu!
Inhaltsübersicht
Lagebeziehungen von Geraden einfach erklärt
Die zwei Geraden g und h können in einem dreidimensionalen Raum vier verschiedene Lagebeziehungen haben:
- Identisch: Alle Punkte der Gerade g sind auch Punkte der Gerade h.
- Echt parallel: Die Gerade g und h haben keine gemeinsamen Punkte und ihre Richtungsvektoren sind linear abhängig. Verschiebst du die Geraden aufeinander, dann sind sie identisch.
- Windschief: Es gibt keine gemeinsamen Punkte von der Gerade g und h. Ihre Richtungsvektoren sind linear unabhängig.
- Sich schneidend: Die Geraden g und h haben genau einen gemeinsamen Punkt, den Schnittpunkt.
Lagebeziehungen bestimmen — Anleitung
Möchtest du die Lagebeziehungen von Geraden im Raum bestimmen, dann folge dieser Schritt-für-Schritt-Anleitung:
-
Lineare Abhängigkeit
der Richtungsvektoren überprüfen:
Schau dir den Richtungsvektor der Gerade g an. Überlege, ob du ihn mit einer Zahl multiplizieren oder dividieren kannst, um auf den Richtungsvektor der Gerade h zu kommen.
→ Ist das der Fall, dann sind die Richtungsvektoren ein Vielfaches voneinander und somit linear abhängig. Rechne nun bei 2.1 weiter.
→ Ist das nicht möglich, dann sind die Richtungsvektoren linear unabhängig. Wenn du diesen Fall gegeben hast, mache bei Schritt 2.2 weiter.
- Genaue Lagebeziehung bestimmen:
2.1. Punkt einsetzen: Sind die Richtungsvektoren linear abhängig, dann sind die Geraden g und h entweder identisch oder parallel. Um das herauszufinden, setzt du einen Punkt der Gerade g in die Gerade h ein.
→ Liegt der Punkt auf der Gerade h, dann sind die Geraden identisch.
→ Haben sie keinen gemeinsamen Punkt, sind die Geraden parallel.
2.2. Geraden gleichsetzen: Sind die Richtungsvektoren linear unabhängig, dann sind die Geraden g und h entweder windschief oder sie schneiden sich. Hier setzt du die beiden Geradengleichungen gleich.
→ Kannst du dieses lineare Gleichungssystem lösen, dann schneiden sich die Gerade g und h.
→ Ist das Gleichungssystem unlösbar, dann sind die Geraden g und h windschief.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lagebeziehung bestimmen — Beispiel
Probiere die Schritt-für-Schritt-Anleitung direkt an einem Beispiel: Berechne, welche Lagebeziehung die Gerade g und h zueinander haben.

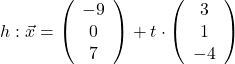
-
Lineare Abhängigkeit der Richtungsvektoren überprüfen:
 ≠
≠ 
Die Richtungsvektoren sind linear unabhängig. Du kannst keine Zahl für s einsetzen, sodass die Vektoren gleich werden.
- 2. Genaue Lagebeziehung bestimmen:
Die beiden Geraden sind also entweder windschief oder sie schneiden sich in einem Punkt. Um das herauszufinden, stellst du ein lineares Gleichungssystem auf und löst es:
l: s = -9 + 3t
ll: 8 + 2s = t
lll: -7 – 2s = 7 – 4t
→ l in ll einsetzen :
8 + 2 · (-9 + 3t) = t
8 – 18 + 6t = t
-10 = -5t | : (-5)
2 = t
→ t in l einsetzen:
s = -9 + 3 · 2
s = -9 + 6
s = -3
→ t und s in lll einsetzen:
-7 – 2 · (-3) = 7 – 4 · 2
-7 + 6 = 7 – 8
-1 = -1
⇒ Das lineare Gleichungssystem ist lösbar. Die Geraden schneiden sich also in einem Punkt.
-
Schnittpunkt bestimmen:
Setze dafür entweder den berechneten Wert für s in die Gerade g oder den Wert für t in die Gerade h ein. Hierbei ist es egal, für welche Variante du dich entscheidest. Es kommt jeweils der gleiche Schnittpunkt heraus.

Die Geraden g und h schneiden sich im Punkt (-3 | 2 | -1).
Lagebeziehungen von Geraden — häufigste Fragen
-
Welche Lagebeziehungen von Geraden gibt es?
Wenn die Richtungsvektoren von zwei Geraden identisch sind, dann sind sie entweder parallel oder identisch. Sollten die Richtungsvektoren linear unabhängig sein, dann sind die Geraden windschief oder sie schneiden sich.
-
Wie kann ich die Lage zweier Geraden erkennen?
Du kannst die Lage von Geraden erkennen, indem du die Richtungsvektoren betrachtest. Kannst du durch Multiplikation oder Division mit einer Zahl den einen Richtungsvektor in den anderen umwandeln, dann sind sie linear abhängig. Das zeigt dir, dass die Geraden identisch oder echt parallel sind. Ist das nicht der Fall, dann sind sie windschief oder sie schneiden sich.
Abstand Gerade Gerade
Super! Du weißt jetzt, welche unterschiedlichen Lagebeziehungen es gibt und wie du sie bestimmst. Möchtest du jetzt den Abstand zweier Geraden berechnen? Dann schau im Video dazu vorbei!
