Video

Quiz

Hier geht's zum Video „Potenzregel und Faktorregel“

Hier geht's zum Video „Negative Potenzen“

Hier geht's zum Video „Produktregel“

Hier geht's zum Video „Kettenregel“

Hier geht's zum Video „Ableitungsregeln“

Ableitungen Übungen

Wichtige Inhalte in diesem Video

Ableitung Übungen mit Prozentregel

Ableitungen Aufgaben mit Brüchen

Übungsaufgaben Ableiten einer e-Funktion

Ableitung Übungen mit Logarithmus

Du wiederholst gerade das Thema Ableitung und suchst noch nach ein paar Ableitungsübungen mit Lösungen? Dann bist du hier und im Video genau richtig. Wir zeigen dir verschiedene Aufgaben und wie du sie löst.

Inhaltsübersicht

Ableitung Übungen mit Prozentregel

im Videozur Stelle im Video springen

Bilde die Ableitung folgender Funktionen. Beachte dabei die Potenzregel :

f(x) = 5x + 2
f(x) = 3x²
f(x) = 5x³ + 2x
f(x) = $\sqrt{x}$
f(x) = 3x⁴ – 2x³ + 8x² – 6x + 4

Lösungen

Die Potenzregel beschreibt, wie du einen Term mit der Form xⁿ ableitest. Du multiplizierst das x mit der Hochzahl und rechnest die Hochzahl – 1.

xⁿ ⇒ n • x^n-1

f(x) = 5x + 2
f'(x) = 5 • 1 • x^1-0 = 5 • x⁰ = 5
f(x) = 3x²f'(x) = 2 • 3x^2-1 = 6x
f(x) = 5x³ + 2x
f'(x) = 3 • 5x² + 2
f(x) = $\sqrt{x} = x^{\frac{1}{2}}$

Um die Ableitung von $\sqrt{x}$ bilden zu können, forme die Wurzel in eine Potenz um. Dann kannst du die Potenzregel anwenden, um die Ableitung zu bilden.

f'(x) = $\frac{1}{2} \cdot x^{-\frac{1}{2}}$
f(x) = 3x⁴ – 2x³ + 8x² – 6x + 4

Da die einzelnen x-Terme mit einem Plus oder Minus verbunden sind, kannst du jede Ableitung einzeln bilden und wieder mit einem Rechenzeichen aneinanderfügen.

f'(x) = 4 • 3x^4-1 – 3 • 2x^3-1 + 2 • 8 • x^2-1 – 6 • x^1-1f'(x) = 4 • 3x³ – 3 • 2x² + 2 • 8 • x¹ – 6 • x⁰f'(x) = 12x³ – 6x² + 16x – 6

Ableitungen Aufgaben mit Brüchen

im Videozur Stelle im Video springen

Bei einer Funktion kann die Variable, nach der du ableitest, auch im Nenner eines Bruches stehen.

f(x) = $\frac{1}{x}$
f(x) = $\frac{2}{x^2}$
f(x) = $\frac{1}{x^2} + 3x^{-1}$

Lösungen

Wandle bei Aufgaben mit Brüchen den Bruch zuerst in eine Potenz um:

f(x) = $\frac{1}{x}$ = x^-1

Nachdem du den Bruch in eine Potenz umgewandelt hast, kannst du wieder die Potenzregel anwenden. Du multiplizierst das x mit der Hochzahl und rechnest die Hochzahl – 1.

f'(x) = -1 • x^-2 = $-\frac{1}{x^2}$
f(x) = $\frac{2}{x^2}$ = 2 • x^-2f'(x) = -2 • 2 • x^-3 = -4 • x^-3 = $-\frac{4}{x^3}$
f(x) = $\frac{1}{x^2} + 3x^{-1}$ = x^-2 + 3x^-1

f'(x) = -2 • x^-2-1 + (-1) • 3 • x^-1-1f'(x) = -2 • x^-3 + (-1) • 3 • x^-2f'(x) = -2x^-3 – 3x^-2

Übungsaufgaben Ableiten einer e-Funktion

im Videozur Stelle im Video springen

Leite die folgenden e-Funktionen ab. Achte dabei auf die Ableitungsregeln und die Produktregel :

f(x) = e^x
f(x) = e^-x
f(x) = e^4x
f(x) = $e^{x^2}$
f(x) = $e^{\sqrt{x}}$
f(x) = x² • $e^{-\sqrt{x}}$

Lösungen

f(x) = e^x
Die Funktion e^x bleibt bei der Ableitung unverändert.

f'(x) = e^x
f(x) = e^-xf'(x) = -1 • e^-x
f(x) = e^4xf'(x) = 4 • e⁴^x
f(x) = $e^{x^2}$
f'(x) = 2x • $e^{x^2}$
f(x) = $e^{\sqrt{x}}$ = $e^{x^{\frac{1}{2}}$

f'(x) = $\frac{1}{2} \cdot x^{-\frac{1}{2}} \cdot e^{x^{\frac{1}{2}}}$
f'(x) = $\frac{1}{2} \cdot \frac{1}{\sqrt{x}} \cdot e^{\sqrt{x}}$
f(x) = x² • $e^{-\sqrt{x}} = x^2 \cdot e^{-x^{\frac{1}{2}}$

Um diese Aufgabe zu lösen, brauchst du die Produktregel. Bestimme also zuerst u(x) und v(x) und deren Ableitungen:

u(x) = x² ⇒ u'(x) = 2x
v(x) = $e^{-\sqrt{x}} = e^{-x^{\frac{1}{2}}$ ⇒ v'(x) = $-\frac{1}{2} \cdot x^{-\frac{1}{2}} \cdot e^{-\sqrt{x}}$

f'(x) = u'(x) • v(x) + u(x) • v'(x) → Produktregel
f'(x) = $\textcolor{teal}{2x} \cdot \textcolor{blue}{e^{-\sqrt{x}}} + \textcolor{red}{x^2} \cdot \left(\textcolor{orange}{-\frac{1}{2} \cdot x^{-\frac{1}{2}} \cdot e^{-\sqrt{x}}}\right)$
f'(x) = $2x \cdot e^{-\sqrt{x}} - \frac{1}{2} \cdot x^2 \cdot x^{-\frac{1}{2}} \cdot e^{-\sqrt{x}}$
f'(x) = $2x \cdot e^{-\sqrt{x}} - \frac{1}{2} \cdot x^{\frac{3}{2}} \cdot e^{-\sqrt{x}}$

Ableitung Übungen mit Logarithmus

im Videozur Stelle im Video springen

Versuche die Ableitungsübungen mit Logarithmus.

f(x) = ln(x)
f(x) = x • ln(x)
f(x) = ln(-x)
f(x) = ln(x²)
f(x) = ln $\left(\frac{1 + e^x}{1 - e^x} \right)$

Lösungen

Wende wenn nötig die Kettenregel an:

f(x) = ln(x)
f'(x) = $\frac{1}{x}$
f(x) = x • ln(x)

u(x) = x ⇒ u'(x) = 1
v(x) = ln(x) ⇒ v'(x) = $\frac{1}{x}$

f'(x) = u'(x) • v(x) + u(x) • v'(x)
f'(x) = 1 • ln(x) + x • $\textcolor{orange}{\frac{1}{x}}$
f'(x) = ln(x) + 1
f(x) = ln(-x)
f'(x) = (-1) • $\frac{1}{-x} = \frac{1}{x}$
f(x) = ln(x²)

Durch das x² in der Klammer des Logarithmus brauchst du für die Ableitung die Kettenregel.

u(x) = ln(x) ⇒ u'(x) = $\frac{1}{x}$
v(x) = x² ⇒ v'(x) = 2x

f'(x) = u'(v(x)) • v'(x) = u'(x²) • v'(x)
f'(x) = $\frac{1}{x^2} \cdot 2x = \frac{2}{x}$
f(x) = ln $\left(\frac{1 + e^x}{1 - e^x} \right)$

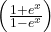
Um die Ableitung dieser Funktion bilden zu können, musst du die Kettenregel anwenden. Bilde dafür die Ableitungen u(x) und v(x):

u(x) = ln(x) ⇒ u'(x) = $\frac{1}{x}$
v(x) = $\frac{1 + e^x}{1 - e^x}$ ⇒ v'(x) = $\frac{e^x \cdot (1-e^x)-(1+e^x) \cdot (-e^x)}{(1 - e^x)^2}$

Für die Ableitung von v(x) musst du die Quotientenregel anwenden:

v'(x) = $\frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}$
v'(x) = $\frac{e^x \cdot (1-e^x)-(1+e^x)\cdot (-e^x)}{(1 - e^x)^2}$

g(x) = 1 + e^x ⇒ g'(x) = e^xh(x) = 1 – e^x ⇒ h'(x) = -e^xHast du die Ableitung v'(x) gebildet, kannst du weiter die Ableitung f'(x) berechnen:

f(x) = u(v(x)) → Kettenregel

f'(x) = (u(v(x)))‘ = u'(v(x)) • v'(x)
f'(x) = u‘ $\left(\frac{1 + e^x}{1 - e^x} \right)\cdot \frac{e^x \cdot (1-e^x)-(1+e^x)\cdot (-e^x)}{(1 - e^x)^2}$
f'(x) = $\frac{1}{\frac{1 + e^x}{1 - e^x}} \cdot \frac{e^x \cdot (1-e^x)-(1+e^x)\cdot (-e^x)}{(1 - e^x)^2}$ → binomische Formel im Nenner

f'(x) = $\frac{e^x -e^{2x} + e^x + e^{2x}}{1 - e^{2x}} = \frac{2e^x}{1-e^{2x}}$

Ableiten Übungen mit Sinus und Cosinus

Auch Sinus und Cosinus kannst du ableiten. Schau dir dazu gleich ein paar Übungen an:

f(x) = sin(x)
f(x) = 2 • cos(x)
f(x) = -sin(x)
f(x) = sin(3x)
f(x) = x • cos(2x – 1)

Lösungen

Die Ableitungen von Sinus und Cosinus lassen sich als Kreis darstellen. Dieser Kreis dient dir als Eselsbrücke:

Sinus, Cosinus, Ableitung, Ableitung Sinus, Ableitung Cosinus, trigonometrische Funktion, trigonometrische Funktion Ableitung — Ableitung Sinus und Cosinus

f(x) = sin(x)

Um die Ableitung des Sinus mithilfe der Kreis Darstellung bilden zu können, gehst du vom sin(x) einen Schritt in Pfeilrichtung weiter. So gelangst du zur 1. Ableitung cos(x).

f'(x) = cos(x)
f(x) = 2 • cos(x)
f'(x) = 2 • (– sin(x)) = -2 • sin(x)
f(x) = – sin(x)
f'(x) = – cos(x)
f(x) = sin(3x) → Kettenregel

Die Ableitung des Terms in der Klammer ist 3. Dieses Teilergebnis multiplizierst du mit der Ableitung des Sinus.

f'(x) = 3 • cos(3x)
f(x) = x • cos(2x – 1) → Produktregel

u(x) = x ⇒ u'(x) = 1
v(x) = cos(2x – 1) ⇒ v'(x) = 2 • (– sin(2x – 1)) = -2 • sin(2x – 1) → Kettenregel

Nachdem du u(x) und v(x) bestimmt hast, kannst du die Ergebnisse und ihre Ableitungen in die Formel für die Produktregel einsetzen:

f'(x) = u'(x) • v(x) + u(x) • v'(x)
f'(x) = 1 • cos(2x – 1) + x • (-2 • sin(2x – 1))
f'(x) = cos(2x – 1) – 2x • sin(2x – 1)

Aufgabe mit Ableitung

Berechne den Punkt auf der Funktion, an dessen Stelle die Steigung = 0 ist.

f(x) = 3x² + 2x – 4

Funktion, Parabel, Funktion einer Parabel, Tiefpunkt berechnen, Steigung berechnen, Steigung einer Funktion, Tangente, Ableitung, Ableitung einer Parabel — Funktion einer Parabel

Lösung:

Die Steigung an einer bestimmten Stelle der Parabel findest du mithilfe der 1. Ableitung heraus:

f'(x) = 6x + 2

Um den Punkt zu bestimmen, an dem die Steigung = 0 ist, setzt du die 1. Ableitung gleich 0:

$\begin{align*} f'(x) &= 0 \\ 6x+ 2 &= 0 \\ 6x &= -2 \\ x &= -\frac{2}{6} = -\frac{1}{3} \end{align*}$

Die Funktion f(x) hat an der Stelle x = $\textcolor{red}{-\frac{1}{3}}$ die Steigung 0. Graphisch kannst du das ermitteln, indem du den Tiefpunkt der Funktion bestimmst und einzeichnest.

Waagerechte Tangenten

Bestimme alle Punkte, an denen die Funktion f(x) = 1/3x³ + 4x² + 3x + 8 eine waagerechte Tangente besitzt:

Tangente, Tangente einer Funktion, Tangente einer Funktion berechnen, Tangente berechnen, Funktion, Hochpunkt, Tiefpunkt — Punkte mit einer waagerechten Tangente

Lösung:

Dazu bestimmst du zuerst die 1. Ableitung der Funktion f(x):

f'(x) = x² + 8x + 3

Da die 1. Ableitung die Steigung der Funktion f(x) an einer bestimmten Stelle beschreibt, setzt du f'(x) = 0:

f'(x) = 0
x² + 8x + 3 = 0
1x² + 8x + 3 = 0

Weil es sich um eine quadratische Gleichung handelt, brauchst du die Mitternachtsformel , um die beiden Lösungen zu berechnen. Bestimme dafür a, b und c, die du dann in die Formel einsetzt:

a = 1 und b = 8 und c = 3

x_1,2 = $\frac{-\textcolor{olive}{b} \pm \sqrt{\textcolor{olive}{b}^2 - 4\textcolor{magenta}{a}\textcolor{orange}{c}}}{2\textcolor{magenta}{a}} = \frac{-\textcolor{olive}{8} \pm \sqrt{\textcolor{olive}{8}^2 - 4 \cdot \textcolor{magenta}{1} \cdot \textcolor{orange}{3}}}{2 \cdot \textcolor{magenta}{1}}$

x₁ = -0,4 und x₂ = -7,6

Die Funktion f(x) hat an der Stelle x₁ = -0,4 und x₂ = -7,6 einen Tiefpunkt bzw. Hochpunkt, und somit eine waagerechte Tangente.

Textaufgabe mit Ableitung

Die Funktion f(x) = -0,02x³ – 0,09x² + 1,35x + 7,5 beschreibt im Intervall [-10; 6] eine Achterbahnfahrt. Berechne die beiden Stellen, an denen der Achterbahnwagon waagerecht steht.

Funktion 3. Grades, Funktion, Funktionsgleichung, Hochpunkt, Tiefpunkt, Extremwerte, Ableitung, Extremwerte mit Ableitung berechnen, Steigung, Steigung gleich 0, Steigung mit Ableitung berechnen — Verlauf der Achterbahn

Lösung:

Ein waagerechter Achterbahnwagon befindet sich an einer Stelle der Achterbahn, an der die Steigung gleich 0 ist. Um diese Stelle herauszufinden, musst du die 1. Ableitung der Funktion gleich 0 setzen.

f'(x) = -0,02 • 3 • x² – 0,09 • 2 • x + 1,35

f'(x) = 0
-0,02 • 3 • x² – 0,09 • 2 • x + 1,35 = 0
-0,06x² – 0,18x – 1,35 = 0

Nun brauchst du die Mitternachtsformel:

a = -0,06 und b = -0,18 und c = 1,35

x_1,2 = $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-(-0,06) \pm \sqrt{(-0,18)^2 - 4 \cdot (-0,06 \cdot 1,35}}{2 \cdot (-0,06)}$

x₁ = -6,47 und x₂ = 3,47

Der Achterbahnwagon befindet sich an den Stellen x₁ = -6,47 und x₂ = 3,47 in waagerechter Position. Aus dem Graph der Funktion kannst du erschließen, dass es sich bei x₁ um einen Tiefpunkt und bei x₂ um einen Hochpunkt der Funktion f(x) handelt.

Tangente an einer bestimmten Stelle berechnen

Bestimme die Tangente g(x) an der Stelle x = 2 der Funktion f(x) = -x² + x + 10.

Steigung berechnen, Steigung einer Parabel berechnen, Steigung einer Parabel, Steigung an einer bestimmten Stelle, Steigung einer Funktion, Tangente, Tangente berechnen, Tangente einer Parabel, Steigung einer Tangente — Steigung an der Stelle x=2

Lösung:

Um die Steigung einer Funktion berechnen zu können, brauchst du die 1. Ableitung dieser Funktion.

f'(x) = -2 • x + 1

Die Steigung der Tangente g(x) an einer Stelle x hat die selbe Steigung wie die Funktion f(x) an dieser Stelle. Setze deshalb x = 2 in die 1. Ableitung ein, um die Steigung zu bestimmen.

f'(2) = -2 • 2 + 1 = -4 +1 = -3

Die Steigung m = -3 setzt du dann in die Geradengleichung y = mx + b ein.

g(x): y = -3 • x + b

Um die Funktion der Tangente fertig bestimmen zu können, setzt du einen Punkt für x und y ein, der sowohl auf der Funktion f(x) als auch auf der Tangente g(x) liegt. Damit du diesen Punkt berechnen kannst, setzt du x = 2 in die Funktionsgleichung f(x) ein:

f(2) = -2² + 2 + 10 = -4 + 2 + 10 = 8
P(2 | 8)

Diesen Punkt setzt du dann in die Tangente g(x) ein, um den y-Achsenabschnitt b berechnen zu können:

8 = -3 • 2 + b
8 = -6 + b
b = 14

Die Gleichung g(x) der Tangente sieht also so aus: y = -3 • x + 14

Ableitung Sinus

Prima! Du hast einige Beispiele zum Thema Ableitung gerechnet. Willst du die Theorie zu den Ableitungsregeln noch einmal wiederholen? Dann schau direkt in unserem Video dazu vorbei!

Zum Video: Ableitungsregeln

zur Videoseite: Ableitungen Übungen

Beliebte Inhalte aus dem Bereich Mathe Grundlagen

Zweite Ableitung

Ableitung bestimmter Funktionen

Ableitungen Übungen

Graphisches Ableiten

Hinreichende Bedingung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .