Dreisatz
Der Dreisatz ist ein Verfahren, mit dem du das Verhältnis zwischen zwei Größen bestimmen kannst. Hier erklären wir dir, wie du den Dreisatz anwendest.
Inhaltsübersicht
Dreisatz einfach erklärt
Mit dem Dreisatz kannst du Verhältnis-Aufgaben wie diese lösen: Wenn 4 Äpfel 2 Euro kosten, wie viel Kosten dann 10 Äpfel?
Das ist ein Beispiel für einen proportionalen Dreisatz. Hier gilt die Regel: „Je mehr, desto mehr“. Das bedeutet, wenn die eine Größe mehr wird, wird auch die andere Größe mehr.
Je mehr Äpfel du haben möchtest, desto mehr Geld musst du auch bezahlen.
Du kannst den Dreisatz aber auch benutzen, um herauszufinden, wie lange du zum Aufräumen nach deiner Geburtstagsfeier brauchst.
Je mehr Leute dir helfen, desto weniger Zeit benötigt ihr.
In diesem Beispiel hast du einen antiproportionalen Dreisatz. Dabei gilt die Regel: „Je mehr, desto weniger“. Das heißt, wenn du mehr von der einen Größe hast, dann hast du weniger von der anderen.
Proportionaler oder antiproportionaler Dreisatz?
Du weißt nun, dass es zwei Arten vom Dreisatz gibt. Bevor du also eine Aufgabe berechnen kannst, musst du dir immer überlegen, ob du einen proportionalen oder antiproportionalen Dreisatz vor dir hast. Sieh dir dafür ein paar Beispiele an:
Proportionaler Dreisatz:
- Einkaufen und Geld: Je mehr Lebkuchen du kaufst, desto mehr kostet dein Einkauf.
- Menge an Zutaten und Portionen: Je mehr Zutaten du beim Backen oder Kochen benutzt, desto mehr Portionen bekommst du hinterher raus.
Antiproportionaler Dreisatz:
- Geschwindigkeit und Fahrtzeit: Je mehr Geschwindigkeit dein Auto hat, desto weniger Zeit benötigst du für die Fahrt.
- Arbeitsdauer und Mitarbeiter: Je mehr Mitarbeiter im Supermarkt die Regale einräumen, desto weniger Zeit benötigen sie.
Kein Dreisatz: Es gibt auch Situationen, in denen du keinen Dreisatz anwenden kannst.
- Alter und Größe: Je nach dem wie alt du bist, wächst du unterschiedlich viel. Kinder wachsen sehr schnell, während ältere Menschen sogar wieder an Größe verlieren. Du kannst hier also weder „je älter, desto größer“ noch „je älter, desto kleiner“ sagen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel: Proportionaler Dreisatz
Damit du die Rechenschritte beim proportionalen Dreisatz noch besser verstehst, schau dir die Schritt-für-Schritt-Anleitung an einem Beispiel an:
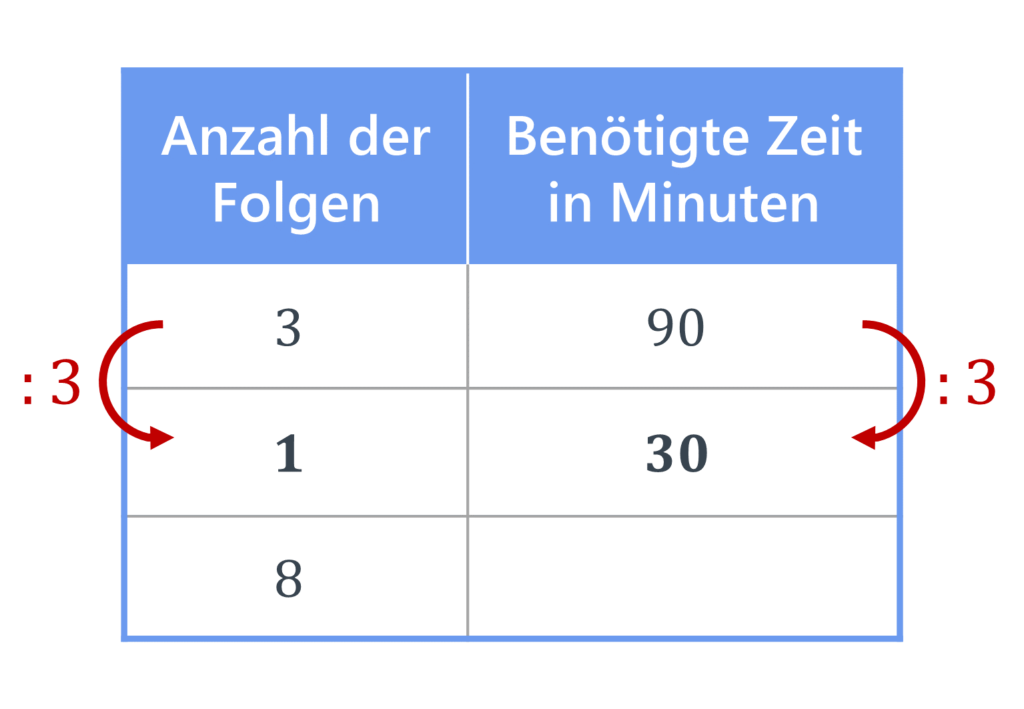
Stell‘ dir vor, 3 Folgen deiner Lieblingsserie dauern insgesamt 90 Minuten. Nun möchtest du wissen, wie viele Minuten 8 Folgen dauern.
Um auf das Ergebnis zu kommen, wendest du den Dreisatz an.
Zunächst musst du entscheiden, ob du die Rechenschritte für den proportionalen oder den antiproportionalen Dreisatz benötigst. Dafür siehst du dir die Aufgabenstellung genau an.
Bei unserem Beispiel ist es so: Je mehr Folgen deiner Lieblingsserie du ansiehst, desto mehr Zeit brauchst du. Du befindest dich also im „je mehr, desto mehr“- Fall und musst die Rechenschritte für den proportionalen Dreisatz anwenden.
Proportionaler Dreisatz: Schritt 1
Starte also mit der Berechnung:
In einem ersten Schritt zeichnest du eine kleine Tabelle mit zwei Spalten und drei Zeilen. In die erste Zeile schreibst du alles, was du bereits weißt. In unserem Fall sind das 3 Folgen, die 90 Minuten dauern.
In die letzte Zeile trägst du außerdem die Mengenangabe der Größe ein, für die du das Verhältnis berechnen möchtest. Das sind also die 8 Folgen, für die du die benötigte Zeit herausfinden willst.
Zwischen der ersten und der letzten Zeile lässt du eine Zeile frei – die brauchst du gleich für einen Zwischenschritt.
Proportionaler Dreisatz: Schritt 2
Nun folgt der zweite Schritt. Rechne aus, wie viel eine einzige Einheit dieser Größe ist. In unserem Beispiel berechnest du, wie viele Minuten eine einzelne Folge dauert.
Um das Ergebnis zu erhalten, teilst du beide Werte in der ersten Zeile durch die Anzahl der Folgen in der ersten Zeile. Das heißt, du rechnest sowohl die 3 Folgen als auch die 90 Minuten durch 3. Das Ergebnis der beiden Rechnungen notierst du in der zweiten Zeile der Tabelle:
90 : 3 = 30
1 Folge dauert also 30 Minuten.
Tipp: Wenn du dir nicht sicher bist, für welche Größe du das Verhältnis für eine einzige Einheit berechnen musst, dann merke dir: In der Tabelle muss die 1 immer in der Spalte stehen, in der du in der dritten Zeile schon einen Wert eingetragen hast.
Proportionaler Dreisatz: Schritt 3
Mit dem dritten Schritt berechnest du den letzten fehlenden Wert in der Tabelle. Um den Wert zu erhalten, nimmst du die zweite Zeile der Tabelle mit dem Wert mal, der bereits in der dritten Zeile steht. Rechne also:
30 · 8 = 240
Den gefundenen Wert trägst du in das freie Feld in der dritten Zeile der Tabelle ein. So hast du auch schon dein Ergebnis: 8 Folgen dauern insgesamt 240 Minuten!
Gar nicht so aufwendig, oder?
Übrigens: Mit demselben Prinzip könntest du auch berechnen, wie viele Folgen du in einer vorgegebenen Zahl an Minuten anschauen kannst.
Die drei Schritte beim Dreisatz
- Schreibe alles auf, was du über beide Größen weißt.
- Berechne das Verhältnis für eine einzige Einheit der einen Größe.
- Bestimme nun das Verhältnis zwischen den beiden Größen für eine der Mengenangaben.
Beispiel: Antiproportionaler Dreisatz
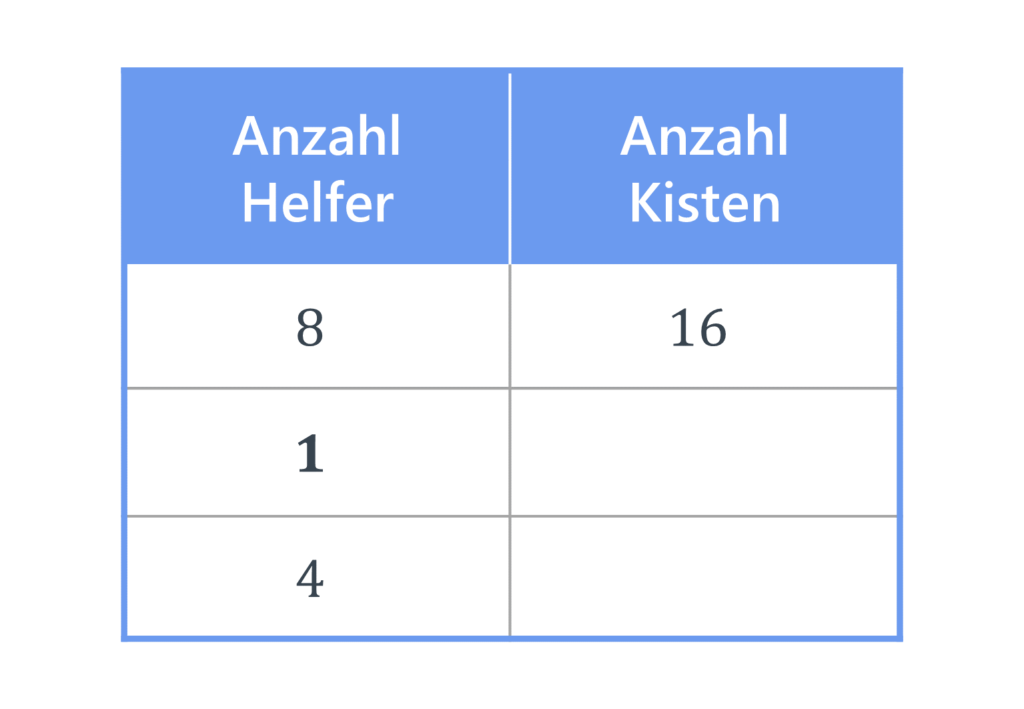
Stell dir vor, du erklärst dich bereit, bei einem Umzug ein paar Kisten zu tragen. Geplant ist, dass insgesamt 8 Personen beim Umzug mithelfen. Jeder Helfer müsste dann 16 Kisten tragen. Leider haben 4 Helfer aber plötzlich doch keine Zeit.
Wie viele Kisten muss nun jeder Helfer tragen, wenn nur noch 4 Personen beim Umzug helfen?
Hier ist es so: Wenn mehr Leute mithelfen, dann muss jede Person weniger Kisten tragen. Du befindest dich also im „je mehr, desto weniger“-Fall. Verwende dafür die Rechenschritte des antiproportionalen Dreisatzes .
Antiproportionaler Dreisatz: Schritt 1
Zeichne wieder eine kleine Tabelle und trage alle Informationen ein, die du bereits kennst.
Bei 8 Helfern muss jede Person 16 Kisten tragen. Diese Angaben schreibst du in die erste Zeile der Tabelle. Die neue Anzahl der Helfer, für die du das Verhältnis berechnen möchtest, ist 4. Diesen Wert trägst du in der dritten Zeile.
Die zweite Zeile der Tabelle lässt du wie vorhin für einen Zwischenschritt frei.
Antiproportionaler Dreisatz: Schritt 2
Rechne aus, wie viele Kisten ein einziger Helfer tragen muss, wenn er beim Umzug ganz alleine wäre. In die zweite Zeile schreibst du auf der Seite der Helfer also eine 1.
Nun fehlt in der zweiten Zeile noch die Anzahl der Kisten. Die Berechnung unterscheidet sich ab hier von den Rechenschritten des proportionalen Dreisatzes.
Statt auf beiden Seiten der Tabelle zu teilen, musst du jetzt nämlich in einer Spalte teilen und in der anderen Spalte malnehmen. Der Grund dafür ist, dass die eine Größe ja mehr wird, wenn die andere Größe weniger wird.
In der Spalte der Helfer steht in der zweiten Zeile bereits eine 1. Um auf dieses Ergebnis zu kommen, wurde die erste Zeile durch 8 geteilt. Du rechnest also in der Spalte der Kisten mal. Die Zahl, mit der du mal oder geteilt rechnest, ist aber in beiden Spalten die gleiche. Folglich musst du den Wert in der Spalte der Kisten mit 8 multiplizieren:
16 · 8 = 128
Eine einzelne Person müsste also ganze 128 Kisten tragen!
Antiproportionaler Dreisatz: Schritt 3
Jetzt hast du es fast geschafft. Berechne in einem letzten Schritt, wie viele Kisten eine Person bei insgesamt 4 Helfern tragen müsste. Auch hierfür rechnest du erneut auf einer Seite der Tabelle mal und auf der anderen Seite geteilt.
Auf welcher Seite du welche Rechenart verwenden musst, kannst du wieder an der linken Spalte der Tabelle ablesen. Du siehst, dass in der letzten Zeile der Tabelle bereits die Zahl 4 eingetragen ist. Um von der zweiten Zeile der Tabelle zur dritten Zeile zu kommen, wurde in dieser Spalte also 1 mal 4 gerechnet. Folglich musst du in der anderen Spalte der Tabelle geteilt durch 4 rechnen, da die Kisten pro Person weniger werden, wenn es mehr Helfer sind:
128 : 4 = 32
Wenn 4 Leute helfen, muss also jede Person 32 Kisten tragen!
Hinweis: Wenn du mehr Rechenschritte zum Dreisatz sehen willst, dann klick in unser nächstes Video zum Dreisatz rein.
Tipps und Tricks für Dreisatzrechnung
Hier haben wir noch einige hilfreiche Tipps für dich zum Dreisatz erklärt:
- Aufgabenstellung: Lies immer genau die Aufgabenstellung und finde die drei gegebenen Zahlen. Finde heraus, ob der Dreisatz proportional oder antiproportional ist.
- Wie rechnet man Dreisatz? Beim Dreisatz rechnen brauchst du eine Tabelle oder die Dreisatz Formel. Dabei kann dir manchmal die schriftliche Multiplikation oder Division helfen. Auch das Einmaleins solltest du können.
- Tabelle: Vor allem am Anfang hilft dir die Dreisatz Tabelle weiter. Später kannst du auch die 3 Satz Formel verwenden.
Dreisatz Übungen
Super! Du weißt jetzt, wie du einen proportionalen Dreisatz berechnest. Du möchtest dein erlerntes Wissen nun üben? Kein Problem! Viele Übungen und Lösungen zum proportionalen und zum antiproportionalen Dreisatz findest du hier .