Stochastische Unabhängigkeit

Unabhängigkeit von Ereigissen

Die stochastische Unabhängikeit von Ereignissen impliziert, dass das Eintreten des einen keine Auswirkung auf die Wahrscheinlichkeit des Eintretens des anderen Ereignisses hat. Man nennt das Ereignis A stochastisch unabhängig von dem Ereignis B, wenn die Wahrscheilichkeit P(A) nicht davon Beeinflusst wird. Dabei ist egal, ob das zweite Ereignis eintritt oder nicht.

direkt ins Video springen

Zum Beispiel hängt die Wahrscheinlichkeit, dass jemand blaue Augen hat, nicht mit der Wahrscheinlichkeit zusammen, dass diese Person die Klausur in Statistik besteht.

Stochastische Unabhängigkeit Formel

Wie man erkennen kann, gilt mathematisch ausgedrückt bei unabhängigen Ereignissen folgendes:

Die bedingte Wahrscheinlichkeit entspricht also genau der unbedingten Wahrscheinlichkeit.

Stochastisch Unabhängig

Das ist ja auch logisch, da das Eintreten von B per Definition keinen Einfluss auf das Eintreten von A hat und umgekehrt. Unter dieser Voraussetzung kann die Wahrscheinlichkeit mit dieser Formel berechnet werden:

direkt ins Video springen

Stochastisch Abhängig

Aber Achtung! Diese Formel kann nur bei unabhängigen Ereignissen verwendet werden. Sind die Ereignisse abhängig, musst du folgende Formel verwenden:

Stochastische Unabhängigkeit Aufgaben

Um Aufgaben zur stochastischen Unabhängigkeit zu lösen, kann man sich zusätzlich verschiedener Hilfsmittel bedienen. Mithilfe dieser kann man die gegebenen Informationen strukturiert abzubilden. Das erleichtert die Berechnung im Anschluss. Eine einfache Vierfelder Tafel oder ein Venn Diagramm  ermöglichen ohne großen Arbeitsaufwand eine bessere Übersicht über die Aufgabenstellung.

Unabhängigkeit im Baumdiagramm

Auch ein Baumdiagramm eignet sich hervorragend dazu die Unabhängigkeit von Ereignissen zu veranschaulichen. Dieses würde zum Beispiel so aussehen:

direkt ins Video springen

Stochastische Unabhängigkeit Beispiel

Schauen wir uns jetzt noch ein passendes Beispiel zur Thematik an. Stell dir vor, ein Würfel wird einmal geworfen. Als Ereignis A legen wir „Ungerade Augenzahl“ und als Ereignis B „Augenzahl kleiner 5“ fest. Jetzt sollst du bestimmen, ob die Ereignisse A und B voneinander abhängig oder unabhängig sind.

direkt ins Video springen

Stochastische Unabhängigkeit berechnen

Zuerst müssen wir die Wahrscheinlichkeit für die beiden Ereignisse bestimmen. Da das Ereignis A drei Elemente umfasst und das Ergebnis B vier, ergibt sich jeweils eine Wahrscheinlichkeit von bzw. .

Als nächstes müssen wir uns überlegen, wie viele Elemente die Schnittmenge von A und B umfasst, also wie viele Elemente sowohl in A als auch in B vorkommen. Das sind die Zahlen 1 und 3.

Dementsprechend ergibt sich für die Schnittmenge von A und B eine Wahrscheinlichkeit von .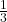

Stochastische Unabhängigkeit prüfen

Jetzt können wir mit der Formel von vorhin einfach überprüfen, ob die Ereignisse voneinander abhängig sind oder nicht. Für unabhängige Ereignisse muss gelten:

In unserem Fall also:

Die Ereignisse A und B sind also statistisch voneinander unabhängig.

Stochastische und kausale Abhängigkeit

Abschließend ist es noch wichtig darauf hinzuweisen, dass stochastische Abhängigkeit nicht das gleiche wie kausale Abhängigkeit ist, die du vielleicht aus deinem Alltag kennst.

direkt ins Video springen

Zwei Ereignisse können nämlich stochastisch abhängig sein, auch wenn sie in Ursache und Wirkung in keiner Beziehung zueinander stehen. Hier findest noch einmal die Formeln, die im Zusammenhang mit unabhängigen Ereignissen wichtig sind:

Für unabhängige Ereignisse gilt: