Wieso können massive Schiffe trotz ihres hohen Gewichts auf dem Wasser schwimmen? Das kannst du mit dem Archimedischen Prinzip erklären. Alles Wichtige dazu zeigen wir dir hier und im Video dazu!
Was ist das Archimedische Prinzip?
Das Archimedische Prinzip ist eine Regel für die Auftriebskraft, welche auf Körper in Medien wie Flüssigkeiten oder Gasen wirkt. Sie besagt, dass die Auftriebskraft des Körpers genau der Gewichtskraft des von ihm verdrängten Mediums entspricht.
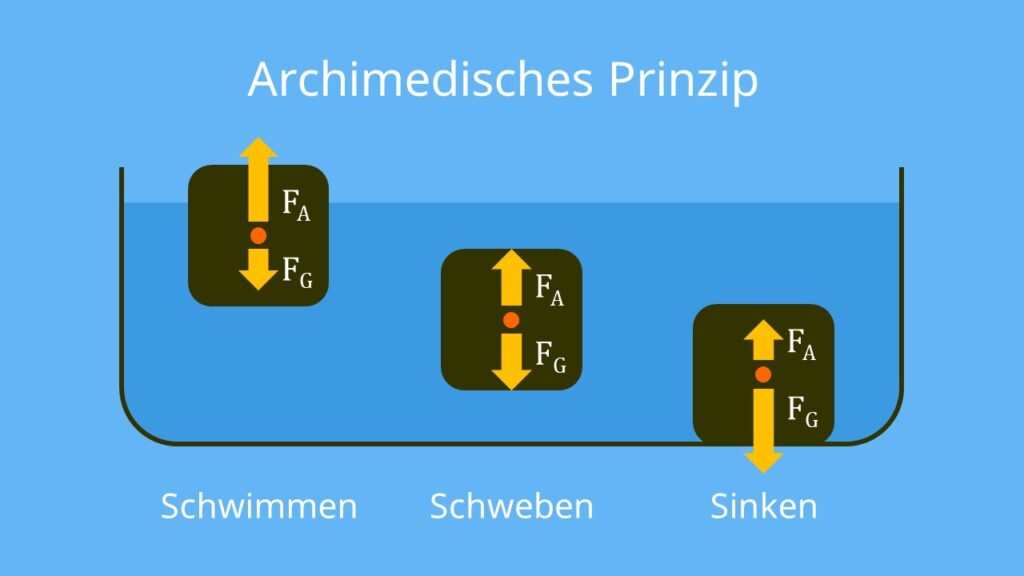
Das erklärt, ob ein Körper in einer Flüssigkeit schwimmt, schwebt oder sinkt. Hierbei spielt der Vergleich von der Auftriebskraft zur Gewichtskraft des Körpers eine große Rolle. Die beiden Kräfte wirken in entgegengesetzte Richtungen.
| Schwimmen | Schweben | Sinken |
| ⇨ Auftriebskraft größer als Gewichtskraft des Körpers | ⇨ Auftriebskraft = Gewichtskraft des Körpers | ⇨ Auftriebskraft kleiner als Gewichtskraft des Körpers |
Bei diesem Vergleich ist auch die Dichte des Mediums wichtig, da die Auftriebskraft von davon abhängig ist. Sie gibt an, wie viele Teilchen sich von einem Medium innerhalb eines bestimmten Raumes befinden.
Achtung: Die Auftriebskraft entspricht der Gewichtskraft des verdrängten Mediums. Das stimmt nicht automatisch mit der Gewichtskraft des Körpers überein.
Die Auftriebskraft eines Objekts in einem Medium entspricht exakt der Gewichtskraft des Mediums, das durch das Objekt verdrängt wird.
Archimedisches Prinzip — Beispiel
Ein typisches Beispiel für das Archimedische Prinzip ist die Wasserverdrängung eines Schiffes. Stell dir dafür vor, dass ein schweres Schiff auf dem Meer schwimmt.
Das Schiff hat eine bestimmte Masse und nimmt im Wasser einen gewissen Raum ein. Dieser Raum stellt das Volumen des Schiffes dar. Das Schiff verdrängt also das Wasser, entsprechend seines Volumens. In diesem Beispiel bildet Wasser somit das verdrängte Medium ab.
Je tiefer das Schiff ins Wasser sinkt, desto mehr Flüssigkeit wird verdrängt. Dadurch steigt die Auftriebskraft so lange an, bis sie der Gewichtskraft des Schiffes entspricht. Laut dem Archimedischen Prinzip entsteht dabei nämlich eine Auftriebskraft nach oben, welche genauso hoch wie die Gewichtskraft des verdrängten Wassers ist.
Durch diese Auftriebskraft kann das schwere Schiff schwimmen. Wenn das Schiff allerdings zu viel beladen hat, kann es trotzdem zum Sinken kommen. In dem Fall kann das Schiff nicht ausreichend Wasser verdrängen, um genug Auftrieb zu erzeugen.
Übrigens: Süßwasser hat eine kleinere Dichte als Salzwasser. Dadurch hat das verdrängte Süßwasser weniger Masse und erzeugt weniger Auftrieb. Deshalb sinken Schiffe in süßeren Gewässern tiefer ein.
Archimedisches Prinzip — Formel
Bei dem Archimedischen Prinzip spielen zwei Kräfte eine zentrale Rolle: die Auftriebskraft nach oben und die Gewichtskraft nach unten des Körpers.
Die Gewichtskraft FG bestimmst du mit folgender Formel:
![\[ F_\mathrm{G} = m \cdot g \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-40a889727e740b9cf148eafa190b9611_l3.png "Rendered by QuickLaTeX.com")
Dabei steht m für die Masse des Körpers und g für die Erdbeschleunigung.
Die Auftriebskraft FA lässt sich durch diese Formel beschreiben:
![\[F_\mathrm{A} = \rho_\mathrm{Medium} \cdot V_\mathrm{Körper} \cdot g\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0c0cc60504f25899ce8a59797bd85f5b_l3.png "Rendered by QuickLaTeX.com")
In dieser Formel ist ρ (rho) die Dichte des Mediums, V das Volumen des Körpers und g die Erdbeschleunigung.
Diese Auftriebskraft entspricht der Gewichtskraft des verdrängten Mediums, also gilt:
![\[ F_\mathrm{G (Medium)} = m_\mathrm{Medium} \cdot g = \rho_\mathrm{Medium} \cdot V_\mathrm{Körper} \cdot g \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ba61346f338eede1507605fc0569f5f8_l3.png "Rendered by QuickLaTeX.com")
Im letzten Schritt kannst du mit einem Vergleich der Auftriebskraft und Gewichtskraft des Körpers ermitteln, ob ein Körper in einer Flüssigkeit sinkt, schwebt oder schwimmt:
![\[ F_\mathrm{A} < F_\mathrm{G} \quad \Longrightarrow \: \textbf{Sinken}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-887a05dbe23800253acc03cf8e997c6d_l3.png "Rendered by QuickLaTeX.com")
![\[ F_\mathrm{A} = F_\mathrm{G} \quad \Longrightarrow \: \textbf{Schweben}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ea1d28d5816bcb47f40fcdf7d168e8a0_l3.png "Rendered by QuickLaTeX.com")
![\[ F_\mathrm{A} > F_\mathrm{G} \quad \Longrightarrow \: \textbf{Schwimmen}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-17e147930e6252294ad7d932fb274ddb_l3.png "Rendered by QuickLaTeX.com")
Archimedisches Prinzip — häufigste Fragen
-
Was ist das Archimedes Prinzip?
Das Archimedes Prinzip besagt, dass ein Körper in einer Flüssigkeit eine Auftriebskraft erfährt, die gleich der Gewichtskraft der verdrängten Flüssigkeit ist.
-
Warum schwimmt ein Schiff?
Schiffe schwimmen, weil das Schiff leichter als das von ihm verdrängte Wasser ist. Dadurch wird die Gewichtskraft des gesamten Schiffs genauso groß wie die Auftriebskraft. Aufgrund des großen Volumen des Schiffes ist das auch trotz hohen Gewichts des Schiffes möglich.
-
Wie lautet das Archimedische Gesetz?
Das Archimedische Gesetz lautet folgendermaßen: Die Auftriebskraft eines Körpers in einem Medium ist genauso groß wie die Gewichtskraft des vom Körper verdrängten Mediums.
Auftriebskraft
Nun weißt du, was das Archimedische Prinzip ist. Die Auftriebskraft nimmt bei dem Prinzip eine wichtige Rolle ein. Woher diese Kraft kommt und wie sie sich genau erklären lässt, erfährst du in diesem Video dazu!
