Totalreflexion
Du möchtest wissen, was eine Totalreflexion ist und wie du den entsprechenden Grenzwinkel berechnen kannst? Dann schau dir unseren Beitrag oder unser Video an.
Inhaltsübersicht
Was ist eine Totalreflexion?
Bei der Totalreflexion wird das komplette Licht am Übergang zwischen zwei Medien reflektiert. Die beiden Medien können zum Beispiel Wasser und Luft sein. Der Lichtstrahl muss dabei aus dem optisch dichteren Medium (Wasser) auf das optisch dünnere Medium (Luft) treffen. Das Licht muss zudem in einem ausreichend flachen Winkel auf das optisch dünnere Medium treffen, damit der Lichtstrahl total reflektiert werden kann.
Wie flach der Einfallswinkel genau sein muss, gibt der sogenannte Grenzwinkel an. Er ist der flachste Winkel, bei dem das Licht noch gebrochen wird. Das bedeutet:
- Beim Grenzwinkel selbst und allen steileren Einfallswinkeln spaltet sich das Licht in einen reflektierten und einen gebrochenen Lichtstrahl auf.
- Bei allen flacheren Einfallswinkel als der Grenzwinkel findet keine Lichtbrechung mehr statt. Es gibt nur noch einen total reflektierten Lichtstrahl.
Totalreflexion beschreibt die vollständige Reflexion eines Lichtstrahls am Übergang von einem optisch dichteren zu einem optisch dünneren Medium. Der Grenzwinkel ist definiert als der Einfallswinkel, bei dem das Licht parallel zur Grenzfläche gebrochen wird. Bei Erhöhung des Einfallswinkel über den Grenzwinkel hinaus, wird der Lichtstrahl totalreflektiert.
Totalreflexion Beispiel in der Natur
Die Totalreflexion kannst du zum Beispiel unter Wasser beobachten, denn Wasser besitzt einen höheren Brechungsindex als Luft.
Beim Tauchen in einem ruhigen Gewässer, ohne Wellen, kannst du die Totalreflexion besonders gut sehen. Unter Wasser musst du die Wasseroberfläche etwas weiter weg von dir beobachten, da die Totalreflexion nur bei flachen Winkeln auftritt. Wenn du also im richtigen Winkel zur Wasseroberfläche hinauf schaust, siehst du eine Spiegelung von allem, was unter Wasser ist, gleichzeitig kannst du aber nicht sehen, was sich über dem Wasser befindet.
Wann entsteht Totalreflexion?
Damit Totalreflexion stattfinden kann, muss der eintreffende Lichtstrahl in einem flachen Winkel auf das optisch dünnere Medium eintreffen.
Wichtig: Der Winkel wird immer zwischen dem einfallenden Lichtstrahl und der Senkrechten gemessen. Das heißt, ein großer Einfallswinkel trifft sozusagen flach auf die Grenzfläche der beiden Medien.
Je nach Einfallswinkel kannst du insgesamt drei Fälle unterscheiden:
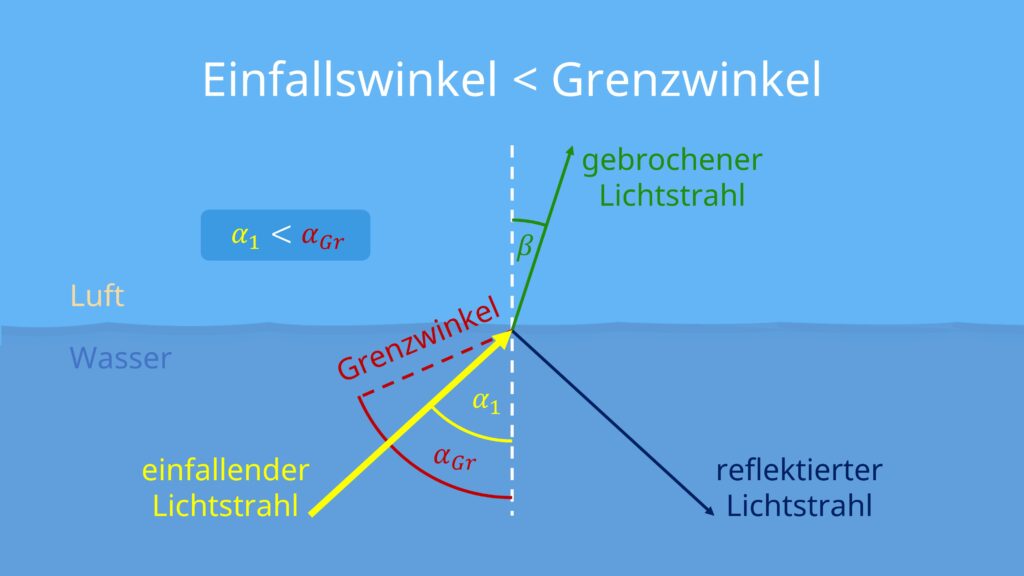
1. Fall: Einfallswinkel < Grenzwinkel
- Einfallswinkel ist kleiner als der Grenzwinkel
- Teil des Lichts wird reflektiert
- Teil des Lichts wird gebrochen
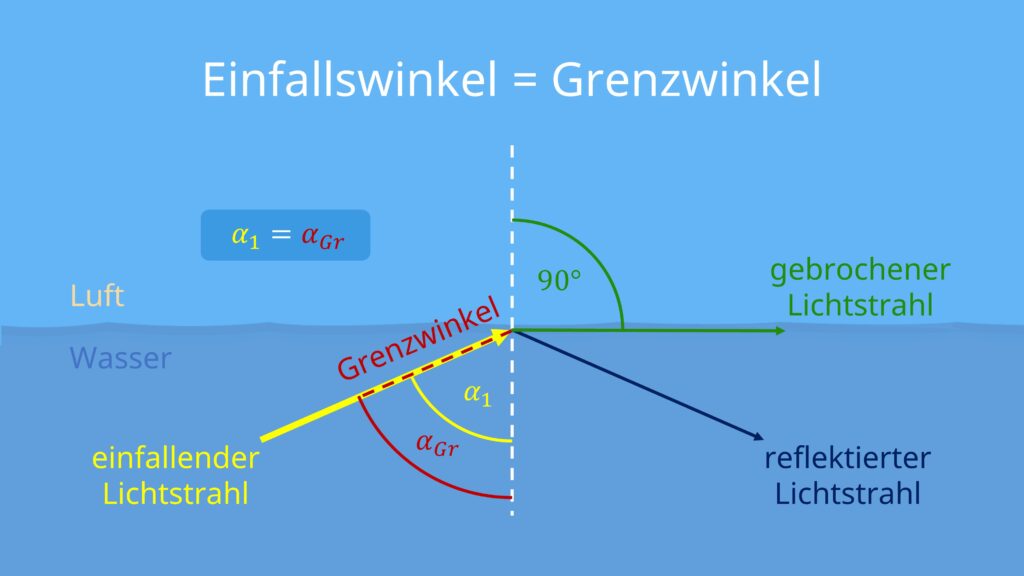
2. Fall: Einfallswinkel = Grenzwinkel
- Einfallswinkel gleich groß wie der Grenzwinkel
- Teil des Lichts wird reflektiert
- Teil des Lichts wird gebrochen
- gebrochener Lichtstrahl verläuft entlang der Grenzfläche
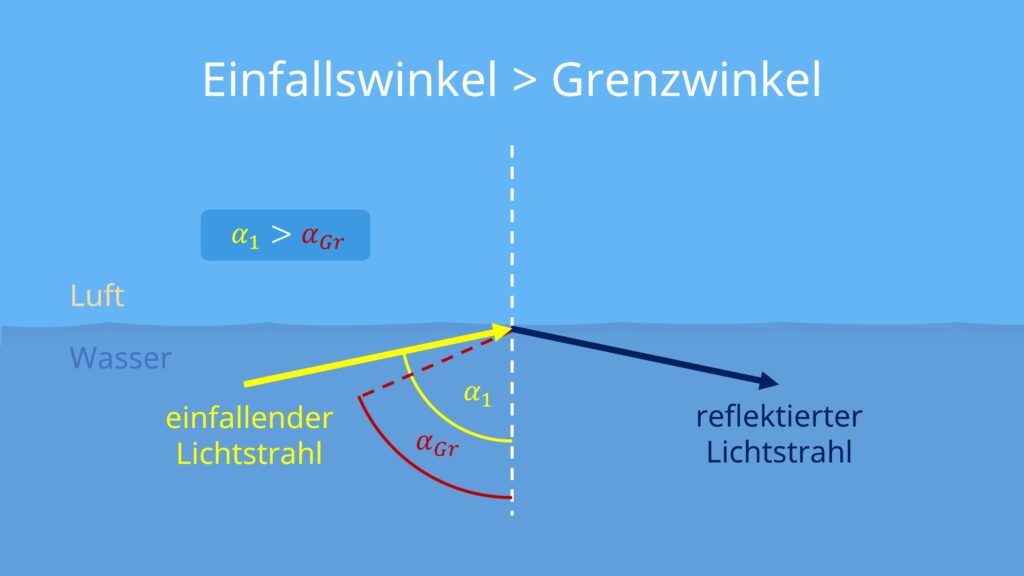
3. Fall: Einfallswinkel > Grenzwinkel
- Einfallswinkel größer als der Grenzwinkel
- Lichtstrahl wird vollständig reflektiert
- keine Lichtbrechung
- Totalreflexion
Wichtig: egal ob eine Totalreflexion stattfindet oder nicht, der reflektierte Strahl verhält sich immer dem Reflexionsgesetz entsprechend. Das bedeutet, für die Reflexion gilt:
- Einfallswinkel gleich Ausfallswinkel
- einfallender Lichtstrahl und reflektierter Lichtstrahl liegen in einer Ebene
- Der Lichtweg ist umkehrbar
Grenzwinkel Formel
Du kannst den Grenzwinkel 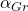 für den Übergang von zwei Medien auch berechnen. Die Formel lautet:
für den Übergang von zwei Medien auch berechnen. Die Formel lautet:
![Rendered by QuickLaTeX.com \[\sin(\alpha_{Gr})= \frac{n_2}{n_1}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cd36ab540eb37edfa023c1699bf680b2_l3.png)
n2 ist dabei der Brechungsindex des optisch dünneren Mediums und n1 der Brechungsindex des optisch dichteren Mediums.
Die Gleichung leitet sich aus dem Brechungsgesetz her. Es lautet:
![Rendered by QuickLaTeX.com \[\frac{sin(\alpha)}{sin(\beta)}=\frac{n_2}{n_1}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8f9ad8a8ca9093f6b01c37e80c91a0bc_l3.png)
Dabei ist α der Einfallswinkel und β der Austrittswinkel des gebrochenen Lichts. Beim Grenzwinkel verläuft der gebrochene Lichtstrahl entlang der Grenzfläche zwischen den beiden Medien. Der Austrittswinkel β beträgt also 90°:
sin(β) = sin(90°) = 1
Daraus folgt, dass der Sinus des Grenzwinkel αGr gleich dem Verhältnis der beiden Brechungsindizes des optisch dünneren (n2) und optisch dichteren Mediums (n1) ist.
Wenn du wissen willst, wie du den Brechungsindex eines Mediums berechnen kannst, dann schau dir unbedingt unseren Beitrag zum Brechungsindex an.
Totalreflexion Beispiel
Mit der Formel kannst du nun den Grenzwinkel für Licht, das von Wasser auf Luft trifft, berechnen. Dafür benötigst nur du die Brechungsindizes der beiden Medien.
Wasser besitzt einen Brechungsindex von n1 = 1,333 und Luft von n2 = 1. Bevor du die Werte in die Formel einsetzen kannst, musst du die Gleichung noch nach dem Grenzwinkel αGr auflösen. Dafür multiplizierst du beide Seiten mit dem Arcussinus und erhältst:
![Rendered by QuickLaTeX.com \[\alpha_{Gr}=arcsin(\frac{n_2}{n_1})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-78e7c9931f71066542fb72797ae5fe31_l3.png)
Nach Einsetzen der beiden Brechungsindizes bekommst du den Grenzwinkel von:
αGr = 48,6°
Anwendungen der Totalreflexion
Die Totalreflexion ist nicht nur im Teilbereich Optik der Physik sehr wichtig, sie wird in vielen technischen Bereichen angewendet. Ein Beispiel sind die sogenannten Lichtleiter.
Lichtleiter, wie zum Beispiel Glasfaserkabel, verwenden die Totalreflexion, um Lichtsignale über lange Strecken zu transportieren. Glasfaserkabel bestehen aus einem Kern und einer Ummantelung. Hierbei ist der Glasfaserkern das optisch dichte Medium und die Ummantelung das optisch dünnere Medium. Aufgrund der Totalreflexion wird das Licht innerhalb des Glasfaserkabels von der Ummantelung fast vollständig reflektiert und bleibt im Kern.
Durch den großen Unterschied der beiden Brechungsindizes der beiden Medien ist der Winkelbereich für eine Totalreflexion sehr groß. Dadurch kannst du Glasfaserkabel auch um Kurven legen, ohne dass die Lichtsignale im Kabel durch Lichtbrechung verloren gehen.
Auch das bekannte Kabelinternet wird mithilfe von Glasfaserkabel übermittelt. Hierbei werden die elektrischen Signale mithilfe von elektrooptischen Wandlern in elektromagnetische Impulse umgewandelt.
Lichtbrechung
Neben der Reflexion ist die Lichtbrechung ein wichtiger Vorgang beim Übergang von Licht zwischen zwei Medien. Schau dir unseren Beitrag zu Lichtbrechung an, um mehr darüber zu erfahren.