Lagrange-Ansatz
Der Lagrange-Ansatz bzw. die Lagrange-Methode ist ein hilfreiches Instrument in der Mikroökonomie, das aber auch in Mathe oder Physik immer wieder verwendet wird. Wir erklären dir in drei einfachen Schritten, wie du mit Hilfe des Lagrange-Multiplikators ganz einfach die Lagrange Funktion aufstellen kannst und damit schnell zum Ziel kommst!
Am einfachsten verstehst du den Lagrange Ansatz wenn du unser Video dazu anschaust! Hier erklären wir dir die Methode anhand eines Beispiels ohne, dass du unseren ausführlichen Artikel lesen musst.
Du möchtest am liebsten gleich los starten und dein Wissen anwenden? Dann schau bei unserer Übungsaufgabe vorbei!
Inhaltsübersicht
Lagrange Funktion
Die Lagrange Funktion löst mathematische Optimierungsprobleme mit mehreren Variablen als Gleichungssystem. Die Zielfunktion muss dabei mindestens so viele Nebenbedingungen wie Variablen umfassen. Joseph-Louis Lagrange fand 1788 mit der Lagrange Funktion eine Methode zur Lösung einer skalaren Funktion durch die Einführung des Lagrange Multiplikators.
Aufstellen und Lösen der Lagrange-Funktion anhand eines Beispiels
Damit du den Lagrange-Ansatz hundertprozentig verstehst, erklären wir dir das Ganze an einem Beispiel. Stell dir vor, dein Chef stellt dir folgende Aufgabe: Für ein Projekt sollst du die optimale Verteilung von Aushilfen und Festangestellten bestimmen. Dazu hast du ein vorgeschriebenes Budget.
Damit du dein Projekt optimal mit Aushilfen und Festangestellten besetzen kannst, verwendest du die Lagrange Methode. Du kannst diese anwenden, wenn du bestimmte Variablen maximieren möchtest. In unserem Beispiel sind es die Festangestellten und Aushilfen. Gleichzeitig gibt es beim Lagrange Verfahren aber eine Nebenbedingung, die die Variablen einschränkt. In unserem Fall ist es das für das Projekt vorgegebene Budget.
Die Lagrange Methode in drei Schritten
So, dann legen wir los: Um die Aufgabe zu lösen, gehst du in drei Schritten vor:
- Zuerst stellst du den Lagrange Ansatz auf.
- Im zweiten Schritt musst du nach jeder Variablen ableiten, sodass du mehrere Ableitungen erhältst.
- Zu guter Letzt hast du ein Gleichungssystem, das du mit ein paar Kniffen lösen kannst.
Lagrange Multiplikator Lambda hinzufügen
Um den Lagrange Ansatz aufzustellen, benötigst du eine Zielfunktion, die du optimieren willst. In unserem Fall ist das der maximierte Nutzen – dazu gleich mehr. Außerdem musst du eine Nebenbedingung beachten. Im Beispiel ist die Nebenbedingung das Budget für das Projekt.
Ein weiterer Bestandteil ist der Lagrange-Multiplikator, der mit dem griechischen Buchstaben Lambda dargestellt wird. Diesen musst du mit der Nebenbedingung multiplizieren.
Machen wir das also direkt für unser Beispiel. Wenn wir jemanden beschäftigen, haben wir einen Nutzen – schließlich arbeitet ja jemand für uns. Daher stellen wir eine sogenannte Nutzenfunktion auf. Weil wir den Nutzen maximieren wollen, ist das unsere Zielfunktion. Typischerweise sieht das dann so aus: Unsere Nutzenfunktion u ist abhängig von 
und 
.
steht dabei für die Aushilfen und für die Festangestellten. Weil Festangestellte in der Regel produktiver sind, haben wir einen größeren Nutzen, wenn wir sie beschäftigen. Deshalb ist die Potenz bei auch etwas höher als bei .
Du hörst zum ersten Mal etwas von Nutzenfunktionen? Dann schau dir doch am besten unser Video zu Nutzenfunktion und Indifferenzkurven an.
Für unser Projekt haben wir ein Budget von 2000€. Das ist also unsere Nebenbedingung. Die Aushilfen bekommen einen Lohn von 100€, während die Festangestellten mit 200€ bezahlt werden.
Unsere Nebenbedingung lässt sich also ganz leicht aufstellen. Wir verteilen das Budget von 2000€ auf eine bestimmte Anzahl an Aushilfen und Festangestellten. Heißt also:
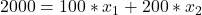
Um gleich mit dem Lagrange-Multiplikator operieren zu können, lösen wir die Nebenbedingung hier nach Null auf.
Das sollte nicht allzu schwer sein. Wir bringen einfach den rechten Term mit Minus auf die andere Seite und dann haben wir‘s auch schon.
Da wir jetzt unsere Zielfunktion u(
) und die Nebenbedingung kennen, können wir endlich unsere Lagrange Funktion aufstellen:
L ist also die Zielfunktion kombiniert mit dem Lagrange Multiplikator, sowie den Nebenbedingungen :
![\[ x_{1}^{0,4} * x_{2}^{0,6} + \lambda (2000 - 100 * x_{1} - 200 * x_{2}) \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-433fd609c04dc6aeb59c1b9fc9f19e60_l3.png "Rendered by QuickLaTeX.com")
Lagrange Funktion ableiten
Im zweiten Schritt müssen wir nach allen Variablen partiell ableiten, die beim Lagrange-Verfahren vorkommen. Das sind für die Aushilfen, für die Festangestellten und der Lagrange-Multiplikator Lambda.
Leiten wir unsere Funktion nach ab, ergibt das:
![\[ $0,4*x_{1}^{-0,6}*x_{2}^{0,6}-100*\lambda \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fb02d05b34dd23790ac17c708e93cccc_l3.png "Rendered by QuickLaTeX.com")
Das Optimum finden wir immer da, wo die Steigung gleich Null ist – wie wenn du beim Bergsteigen den Gipfel erreichst. Deshalb müssen wir die Ableitung gleich Null setzen.
Nach dem gleichen Prinzip funktioniert auch die partielle Ableitung nach .
Wenn dir das mit dem Ableiten zu schnell ging, schau dir nochmal das Video Potenzfunktion ableiten im Bereich Differentialrechnung I an. Danach sollte das mit links klappen.
Bleibt noch die partielle Ableitung nach Lambda, also dem Lagrange-Multiplikator. Die kannst du direkt bestimmen, ohne viel zu rechnen. Der Trick dabei ist, dass die Ableitung nach Lambda einfach die Nebenbedingung ist. Das kannst du also direkt abschreiben.
Aus den partiellen Ableitungen können wir dann drei Gleichungen aufstellen. Die brauchen wir, um im nächsten Schritt und bestimmen zu können. Du solltest dabei immer das Lambda auf eine Seite bringen, damit du es im letzten Schritt einfach rauskürzen kannst.
Bei der ersten partiellen Ableitung addieren wir auf beiden Seiten 100 mal Lambda. 100 lässt sich später auch kürzen, also mach es dir einfach und lass die 100 beim Lambda stehen. Das ist unsere erste Gleichung. Dasselbe machen wir jetzt mit der partiellen Ableitung nach und gehen dabei völlig analog zu vor.
Die Nebenbedingung können wir auch wieder so umformen, dass auf einer Seite das Budget von 2000 € steht.
Du siehst bestimmt schon, dass wir das Lambda nur noch in den ersten beiden Gleichungen finden.
Gleichungssystem lösen – Lagrange-Multiplikator kürzen
Wir haben jetzt also ein Gleichungssystem, das aus drei Gleichungen besteht.
Betrachten wir davon nur mal die erste und die zweite:
Teilen wir Gleichung 1 durch Gleichung 2, dann steht links 100 mal Lambda geteilt durch 200 mal Lambda. Rechts geht das genauso, also einfach untereinander schreiben und den Bruchstrich nicht vergessen!
Jetzt können wir das vereinfachen, indem wir links 100 Lambda und 200 Lambda kürzen. Rechts kommt das 
mit der negativen Potenz, immer auf die andere Seite des Bruchstrichs. Das wandert also nach unten, das nach oben.
Nach aufgelöst bekommen wir dann endlich das Verhältnis von 
. Das ist unsere vierte Gleichung.
Als letzten Schritt brauchen wir nur noch die dritte und die vierte Gleichung. Das setzen wir in unsere Budgetbedingung ein und lösen nach auf.
Es ergibt sich also:
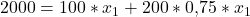
Daraus können wir berechnen, dass gleich 8 ist.
In die vierte Gleichung setzen wir das ein, womit wir für gleich 6 erhalten.
Ziehen wir also ein Fazit: Wir wissen jetzt, dass wir für unser Projekt acht Aushilfen und sechs Festangestellte brauchen. Das haben wir über den Lagrange-Multiplikator mit dem Lagrange-Ansatz berechnet.
Übungsaufgabe
Du möchtest dein Wissen zum Lagrange-Ansatz vertiefen? Dann probiere dich doch an unserer Übungsaufgabe .
