Langfristige Gewinnmaximierung
In diesem Beitrags erklären wir dir kurz und knapp die langfristige Gewinnmaximierung und zeigen dir auch hier anhand eines Beispiels, wie man die langfristige Gewinnmaximierung ganz einfach berechnen kann.
Inhaltsübersicht
Langfristige Gewinnmaximierung: Erklärung und Beispiel
Im Gegensatz zur kurzfristigen Gewinnmaximierung sind hier beide Faktoren variabel. Du musst also beide Faktoren verändern um zu deinem Gewinnmaximum zu kommen.
Die langfristige Gewinnmaximierung ist dabei auch das eigentliche Ziel des Unternehmens, denn eine Unternehmung soll natürlich auf lange Frist möglichst hohe Gewinne erzielen. Kurzfristig muss es nur einen höheren Verkauf anstreben.
Berechnung der langfristigen Gewinnmaximierung
Wie bei der kurzfristigen Gewinnmaximierung, hast du auch hier eine Produktionsfunktion. Diese sieht in unserem Fall so aus:

Nehmen wir an Dein Start-Up produziert Limonade. Deine Produktionsfaktoren könnten dann Wasser in Litern  und Zitronen
und Zitronen  sein. Die Limonade wird zwar so ganz ohne Zucker etwas sauer, aber schmeckt bestimmt trotzdem!
sein. Die Limonade wird zwar so ganz ohne Zucker etwas sauer, aber schmeckt bestimmt trotzdem!
Legen wir noch die Faktorkosten und den Limonaden Preis fest:  ,
,  und p = 15. Wie bei der kurzfristigen Gewinnmaximierung, muss man auch hier wieder den Maximierungssatz aufstellen und alle vorhandenen Informationen einsetzen.
und p = 15. Wie bei der kurzfristigen Gewinnmaximierung, muss man auch hier wieder den Maximierungssatz aufstellen und alle vorhandenen Informationen einsetzen.
Da ja hier beide Faktoren variabel sind, müssen wir den Maximierungssatz auch nach beiden Faktoren ableiten. Wir errechnen also das Grenzprodukt sowohl für die Liter Wasser also auch für die Zitronen und wenden die Optimierungsbedingung an. Diese lautet  und wird auch einfach Inputregel genannt. Das sieht dann so aus:
und wird auch einfach Inputregel genannt. Das sieht dann so aus:
Danach bringen wir die Faktorpreise wieder auf die andere Seite und multiplizieren das jeweilige Grenzprodukt mit dem passenden Produktionsfaktor. Dadurch können wir die ursprüngliche Produktionsfunktion einsetzen und erhalten somit die von y abhängigen Faktoreinsatzmenge. Das sieht wie folgt aus:
Die Berechnung für den Einsatzfaktor Zitrone sieht folgendermaßen aus:
Jetzt stellst du deine Gleichungen noch nach den Produktionsfaktoren um und erhältst die Faktoreinsatzmengen in Abhängigkeit des Outputs:


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Ergebnis der langfristigen Gewinnmaximierung
Damit Du den gewinnmaximierenden Output rausbekommst, setzt du das Ganze in Deine Produktionsfunktion ein:

Und löst es nach y auf:
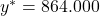
Damit beträgt dein gewinnmaximierendes Output 864.000 Flaschen Limonade!
Jetzt noch  in die Faktoreinsatzmengen in Abhängigkeit des Outputs einsetzten, dann weißt du auch schon, wie viel Wasser und wie viel Zitrone Du brauchst um deinen Gewinn zu maximieren:
in die Faktoreinsatzmengen in Abhängigkeit des Outputs einsetzten, dann weißt du auch schon, wie viel Wasser und wie viel Zitrone Du brauchst um deinen Gewinn zu maximieren:
Du benötigst also für Dein Gewinnmaximum 1.728.000 Liter Wasser und 12.960.000 Zitronen. Um Deinen Gewinn auszurechnen, musst Du alle Deine Werte nur noch in die Gewinnfunktion vom Anfang einsetzten:

Da Du einen Gewinn von 1.080.000€ machst, scheint sich Dein Start-Up ziemlich zu lohnen.
Damit haben wir das Thema der langfristigen Gewinnmaximierung und der kurzfristigen Gewinnmaximierung abgeschlossen.




