Nutzenmaximierung
Du bist dir nach der Vorlesung immer noch unsicher, wie du eine Nutzenmaximierung durchführst? Im folgenden Beitrag fassen wir nochmal die wichtigsten Inhalte zusammen, sodass du ohne Sorgen in die nächste Mikro-Vorlesung gehen kannst.
Inhaltsübersicht
Nutzenmaximierung Definition
Unter Nutzenmaximierung versteht man das Ziel des Nachfrageverhaltens von rationalen Wirtschaftsakteuren. Diese versuchen die geeignete Mengenaufteilung von Produkten und Dienstleistungen zu finden, die gerade noch durch ein begrenztes Budget finanziert werden kann und ihren individuellen Gesamtnutzen maximiert.
Nutzenmaximierung in der Haushaltheorie: Grenzrate der Substitution = Preisverhältnis
Du wählst einfach irgendein Güterbündel auf der Budgetgeraden, beispielsweise Burger und Bier. Aber wir wissen ja, dass das Nutzenniveau umso höher ist, je weiter die Indifferenzkurve vom Ursprung entfernt ist. Deswegen möchtest Du hier Deinen Nutzen maximieren. Du willst Dein Geld also genau für das Güterbündel ausgeben, das auf der Indifferenzkurve liegt, die möglichst weit vom Ursprung entfernt ist und mit der Du trotzdem nicht die Budgetrestriktion verletzt. Wir suchen deshalb den Tangentialpunkt zwischen Indifferenzkurve und Budgetrestriktion. Dieser liegt dort, wo die Grenzrate der Substitution mit der Steigung der Budgetgeraden, also dem Preisverhältnis, übereinstimmt.
Du siehst, dass nur die mittlere Indifferenzkurve in Frage kommt, da dort die Budgetrestriktion gerade noch erfüllt ist. Dein nutzenmaximierendes Güterbündel ist also  .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Nutzenmaximierung Beispiel
Um das Problem mathematisch zu lösen, brauchen wir den Lagrange-Ansatz, da wir ja eine Hauptbedingung – die Nutzenfunktion – und eine Nebenbedingung – die Budgetrestriktion – haben. Folgende Schritte musst du wie beim allgemeinen Lagrange-Ansatz durchführen:
- Den Lagrange-Ansatz aufstellen
- Nach allen Variablen ableiten
- Das Gleichungssystem lösen
Wir haben wieder eine Nutzenfunktion, in unserem Fall eine Cobb-Douglas Funktion  , Preise für
, Preise für  ,
,  und ein Budget von
und ein Budget von  gegeben. Hier möchtest Du Deinen Nutzen, die Eiswaffeln
gegeben. Hier möchtest Du Deinen Nutzen, die Eiswaffeln  und Freibadbesuche
und Freibadbesuche  , maximieren, darfst aber gleichzeitig nicht mehr Geld ausgeben, als du hast. Wir müssen also die Budgetrestriktion als Nebenbedingung
, maximieren, darfst aber gleichzeitig nicht mehr Geld ausgeben, als du hast. Wir müssen also die Budgetrestriktion als Nebenbedingung  beachten. Damit wir sie für unseren Lagrange-Ansatz verwenden können, müssen wir sie erstmal zu
beachten. Damit wir sie für unseren Lagrange-Ansatz verwenden können, müssen wir sie erstmal zu  umstellen.
umstellen.
Der erste Schritt der Nutzenmaximierung: Lagrange-Ansatz aufstellen:

Jetzt musst Du ihn nach jeder Variablen einmal ableiten. Also nach  ,
,  und
und  :
:
Nun teilst Du die erste Gleichung durch die zweite. Das sieht dann so aus:
Nutzenmaximierung berechnen
Bestimmt hast Du schon gesehen, dass dieser Teil hier die Grenzrate der Substitution
ist, auch MRS genannt.
Durch Kürzen und Umstellen erhältst Du dann folgende Gleichung:

Jetzt musst Du nur noch Dein Preisverhältnis auf die andere Seite des = bringen… und schon zeigt es dir an, in welchem Verhältnis Deine Freibadbesuche und Deine Eiswaffeln gegeneinander ausgetauscht werden können.

Nun hast Du links die Grenzrate der Substitution, also die Steigung der Indifferenzkurve, und rechts das Preisverhältnis, also die Steigung Deiner Budgetgeraden, stehen. Dann stellst du das Ganze nach einem x um, in unserem Fall am besten nach  .
.

Schauen wir uns zur Sicherheit nochmal an, was wir alles gegeben hatten. Da waren unsere Preise  für das Eis und
für das Eis und  für den Freibadbesuch. Insgesamt haben wir ein Budget von 64. Die gegebenen Preise kannst Du ebenfalls in Deine Gleichung einsetzen:
für den Freibadbesuch. Insgesamt haben wir ein Budget von 64. Die gegebenen Preise kannst Du ebenfalls in Deine Gleichung einsetzen:
Damit hast Du die Optimalitätsbeziehung der beiden Güter. Sie gibt Dir an, in welchem Verhältnis die beiden Güter zueinanderstehen. Das Ganze setzt Du jetzt noch in Deine umgestellte Budgetrestriktion ein:

Da Du ja für Deine Freibadbesuche und Eiswaffeln nur 64€ ausgeben darfst und auch weißt, wieviel beides kostet, kannst Du auch diese Informationen in Deine Gleichung einbringen:
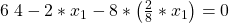
Jetzt musst Du das Ganze nur noch nach  umstellen, dann weißt Du auch schon, wie oft Du Dir diesen Sommer ein Eis leisten kannst:
umstellen, dann weißt Du auch schon, wie oft Du Dir diesen Sommer ein Eis leisten kannst:

Nach der Nutzenmaximierung kannst du also 16 mal ein Eis kaufen. Diese Information setzt Du dann in deine Gleichung für die Optimalitätsbeziehung der beiden Güter ein und erhältst nun auch Deine nutzenmaximierende Anzahl an Freibadbesuchen:

Du kannst also 4 mal ein Freibad besuchen.
Zusammenfassung
Um die Nutzenmaximierung durchzuführen, musst Du Dein nutzenmaximierendes Güterbündel aus Freibadbesuchen und Eiswaffeln errechnen. Der erste Schritt ist also, dass Du den Lagrange – Ansatz mit der Budgetrestriktion als Nebenbedingung aufstellst. Im 2. Schritt leitest Du diesen dann nach allen Variablen ab. Der 3. und letzte Schritt ist etwas aufwändiger: Du teilst die Ableitung nach  durch die Ableitung nach
durch die Ableitung nach  . Dann stellst Du das Ganze nach einer Variablen um. Diese Gleichung setzt Du in die Budgetrestriktion ein und erhältst auch schon den ersten Wert für Dein Güterbündel. Wenn Du den Wert dann in Dein optimales Austauschverhältnis von vorhin einsetzt, erfährst du, wieviel Du für Dein zweites Gut ausgeben solltest.
. Dann stellst Du das Ganze nach einer Variablen um. Diese Gleichung setzt Du in die Budgetrestriktion ein und erhältst auch schon den ersten Wert für Dein Güterbündel. Wenn Du den Wert dann in Dein optimales Austauschverhältnis von vorhin einsetzt, erfährst du, wieviel Du für Dein zweites Gut ausgeben solltest.



