Geometrische Verteilung
Dieser Artikel erklärt einfach und verständlich, was es mit der geometrischen Verteilung auf sich hat. Du erfährst, wann man diese diskrete Verteilung benutzt und wie man die Formeln zur Berechnung des Erwartungswertes, der Dichte und der Verteilungsfunktion verwendet.
Du möchtest wissen, was die geometrische Verteilung mit Bernoulli zu tun hat ohne diesen Artikel zu lesen? Dann sieh dir unser Video zum Thema an!
Inhaltsübersicht
Geometrische Verteilung Statistik
Die Geometrische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, welche sich auf Basis von unabhängigen Bernoulli Experimenten ergibt.
Sie wird oft als „Verteilung des Wartens auf den ersten Erfolg“ bezeichnet. In diesem Ausdruck spiegelt sich auch schon ihre Grundidee wieder. Es liegt ein Bernoulli Experiment mit der Wahrscheinlichkeit p vor und man fragt sich, wie oft man dieses Experiment ausführen muss, bis der erste Erfolg eintritt.
Geometrische Verteilung Beispiel
Ein klassisches Beispiel hierfür ist „Mensch ärgere dich nicht“. Um mit seiner Figur auf das Spielfeld gehen zu dürfen, muss man eine sechs Würfeln. Nun kann man sich fragen, wie oft man würfeln muss, um eine sechs zu erhalten. Jeder Versuch eine sechs zu würfeln ist dabei ein Bernoulli Experiment mit der Wahrscheinlichkeit p= .
.
Mathematisch drückt man die geometrische Verteilung wie folgt aus:
X~G(p)
Beziehungsweise in unserem Beispiel:
X~G(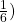
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Geometrische Verteilung Dichte
Die Dichte der geometrischen Verteilung lautet wie folgt:

Warum die Formel so aussieht, kann man sich ganz einfach selbst herleiten. Wenn man beispielsweise die Wahrscheinlichkeit dafür berechnen will, dass man mit dem zweiten Versuch eine 6 würfelt, also f(2), muss man die Wahrscheinlichkeit, dass man im ersten Versuch keine 6 gewürfelt hat, also (1-p), mit der Wahrscheinlichkeit, dass man eine 6 würfelt, also p, multiplizieren. Die Wahrscheinlichkeit im zweiten Versuch eine 6 zu würfeln beträgt also circa 13,89%.

Geometrische Verteilung Verteilungsfunktion
Die Verteilungsfunktion der geometrischen Verteilung lässt sich am einfachsten über die Gegenwahrscheinlichkeit bestimmen. Wir suchen ja die Wahrscheinlichkeit, dass weniger als x Versuche benötigt werden, um eine 6 zu würfeln. Dazu müsste man jede einzelne Wahrscheinlichkeit aufsummieren. Das kann man sich aber sparen, indem man ganz einfach die Wahrscheinlichkeit für das Gegenereignis, also P(X>x) bestimmt. Denn es gilt ja die Regel, dass die Wahrscheinlichkeit 1 minus die Gegenwahrscheinlichkeit ist.

Geometrische Verteilung Varianz
Wenn du den Erwartungswert weißt, ist die Berechnung der Varianz ein Leichtes. Die Formel für die Bestimmung der Varianz sieht wie folgt aus:

Im Endeffekt muss man nur den Erwartungswert einsetzten und erhält im Handumdrehen die gesuchte Varianz.


