Verteilungsfunktion
Wir zeigen dir wie man eine Verteilungsfunktion bestimmen und mit dieser rechnen kann. Zuerst betrachten wir den diskreten und dann den stetigen Fall und es werden jeweils Beispiele für die gängigsten Wahrscheinlichkeitsverteilungen gegeben.
Unsere Videos zu den Themen diskrete Verteilungsfunktion und zu stetige Verteilungsfunktion erklären dir alles zu Verteilungsfunktionen verständlich und in Kürze, sodass du die eingesparte Zeit auf andere Aktivitäten verteilen kannst.
Inhaltsübersicht
Verteilungsfunktion einfach erklärt
Die Verteilungsfunktion gibt an, mit welcher Wahrscheinlichkeit das Ergebnis des Zufallsexperiments kleiner oder gleich eines bestimmten Wertes ist. Dafür werden alle Ergebnisse bis zu diesem Wert aggregiert, also „aufaddiert“. Deshalb spricht man auch oft von einer kumulativen Verteilungsfunktion. Allgemein wird die Verteilungsfunktion mathematisch mit P(X≤x) dargestellt und mit F(x) abgekürzt. Klein x ist dabei der Wert, bis zu dem aggregiert wird. Um eine konkrete Verteilungsfunktion bestimmen zu können, muss man als erstes klären, ob es sich um diskrete Zufallsvariablen oder stetige Zufallsvariablen handelt. Dazu betrachtet man die möglichen Ergebnisse und deren Dichte.
Verteilungsfunktion Dichtefunktion
Liegen uns stetige Zufallsvariablen vor, so wird anhand dieser die Dichtefunktion bestimmt. Bei diskreten Zufallsvariablen hingegen, ermittelt man die Wahrscheinlichkeitsfunktion. Im diskreten Fall wird so die Wahrscheinlichkeit für ein ganz konkretes Ergebnis angegeben.
Wahrscheinlichkeitsfunktion: P(X=x) ≙ „Die Wahrscheinlichkeit, dass das Ergebnis/ Intervall dem Wert x entspricht“
Mit der Dichtefunktion im stetigen Fall lassen sich keine konkreten Wahrscheinlichkeiten bestimmen. Diese gibt lediglich die Dichte, also die Verteilung innerhalb des Intervalls an. Um die Wahrscheinlichkeit für einen bestimmten Abschnitt des Intervalls zu bestimmen, benötigt man die Verteilungsfunktion.
Die kumulative Verteilungsfunktion dagegen gibt also an, mit welcher Wahrscheinlichkeit alle Werte bis zu einem bestimmten Punkt eintreten können. Also zum Beispiel mit welcher Wahrscheinlichkeit du eine Zahl würfelst, die kleiner oder gleich 5 ist.
Verteilungsfunktion: P(X≤x) ≙ „Die Wahrscheinlichkeit, dass das Ergebnis X kleiner gleich dem Wert x ist“
Der Unterschied zwischen Dichte und Verteilungsfunktion liegt also darin, dass die Dichte aussagt, wie die Wahrscheinlichkeiten konkret verteilt sind und die Verteilungsfunktion in einem weiteren Schritt das Integral über alle diese Wahrscheinlichkeiten bildet. Wenn du also die Dichte deiner Zufallsvariablen kennst, kannst du auch ganz einfach die Verteilungsfunktion bestimmen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Quantil Verteilungsfunktion
Anhand der Verteilungsfunktion kannst du außerdem relativ einfach die Werte deiner Verteilung für verschiedene Quantile ablesen. Das Quantil von Zufallsvariablen sagt inhaltlich eigentlich genau dasselbe aus, wie das empirische Quantil von bereits gemessenen Daten. Es teilt den Wertebereich also in 2 Teile, den Bereich „Links“ und den Bereich „rechts“ vom Quantil. Das 50%-Quantil ist also zum Beispiel genau der Wert, der den Wertebereich so aufteilt, dass die Hälfte der Werte kleiner und die andere Hälfte größer als das Quantil sind.
Diskrete Verteilungsfunktion
Die einzelnen Wahrscheinlichkeiten  von diskreten Variablen sind wie gesagt durch die Wahrscheinlichkeitsfunktion gegeben. Um die diskrete Verteilungsfunktion zu erhalten, werden schrittweise alle Wahrscheinlichkeitswerte kumuliert. Das heißt, man bildet das Integral unter der Wahrscheinlichkeitsfunktion.
von diskreten Variablen sind wie gesagt durch die Wahrscheinlichkeitsfunktion gegeben. Um die diskrete Verteilungsfunktion zu erhalten, werden schrittweise alle Wahrscheinlichkeitswerte kumuliert. Das heißt, man bildet das Integral unter der Wahrscheinlichkeitsfunktion.
Beispielsweise beim Würfelwurf ist die Wahrscheinlichkeit, dass eine Augenzahl kleiner gleich 5 gewürfelt wird 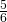 . Um den Funktionswert der Verteilungsfunktion an diesem Punkt zu erhalten, summierst du einfach die Wahrscheinlichkeiten für alle x von 1 bis 5.
. Um den Funktionswert der Verteilungsfunktion an diesem Punkt zu erhalten, summierst du einfach die Wahrscheinlichkeiten für alle x von 1 bis 5.


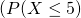 =
=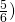
Diskrete Verteilungsfunktion zeichnen
Haben wir die kumulierten Werte der Verteilungsfunktion bestimmt, können wir diese auch zeichnen. Die zugehörige Verteilungsfunktion sieht dann für das Würfelbeispiel so aus:
Der Erwartungswert lässt sich am Graph der Verteilungsfunktion nicht ablesen. Dazu muss man den Graphen der Wahrscheinlichkeits- oder Dichtefunktion betrachten.
Diskrete Verteilungsfunktion berechnen
Um mit der diskreten Verteilungsfunktion zu rechnen, braucht man aber nicht unbedingt die Abbildung des Graphen.
Du bist auf die Gartenparty eines Freundes eingeladen, auf der es unter anderem eine Glücksspielstation mit einem Lostopf gibt. Im Zuge des Spiels zieht man zwei Lose hintereinander.. Ein Los kann entweder ein Gewinn G oder eine Niete N sein. Im Lostopf befinden sich je 2 Gewinnlose ( und
und  ) und 2 Nieten (
) und 2 Nieten ( und
und  ). Die genauen Regeln des Glücksspiels sehen wie folgt aus:
). Die genauen Regeln des Glücksspiels sehen wie folgt aus:
 : Zieht man 2 Nieten, muss man 2€ Strafe zahlen und macht somit 2€ Verlust.
: Zieht man 2 Nieten, muss man 2€ Strafe zahlen und macht somit 2€ Verlust.
 : Zieht man 1 Gewinnlos und eine Niete, erhält man 1€ als Gewinn.
: Zieht man 1 Gewinnlos und eine Niete, erhält man 1€ als Gewinn.
 : Zieht man 2 Gewinnlose, erhält man 2€ als Gewinn.
: Zieht man 2 Gewinnlose, erhält man 2€ als Gewinn.
Da du unter Freunden bist, gibt es keinen Grundeinsatz für das Spiel: du kannst daher nur Gewinn oder Verlust machen.
Nun stellen wir uns folgende Frage: Mit welcher Wahrscheinlichkeit erhalte ich höchstens 1€?
Zieht man wie in unserem Beispiel hier 2 Lose hintereinander, dann ist es essenziell, auch alle Kombinationsmöglichkeiten in den Ergebnisraum mit aufzunehmen, um das Ergebnis und die Wahrscheinlichkeiten nicht zu verfälschen. Unser Ergebnisraum mit der Mächtigkeit 12 sieht also wie folgt aus:

Jedes der 4 Lose kann als erstes gezogen werden. Danach gibt es weitere 3 Möglichkeiten für die Ziehung des zweiten Loses. Daher muss die Mächtigkeit auch rechnerisch bei 4 mal 3 ist gleich 12 liegen.


Nun kannst du die Wahrscheinlichkeiten für die einzelnen Fälle berechnen. Die Wahrscheinlichkeit, dass du 2€ verlierst, liegt bei  und damit ca. 16,7%. Dabei läuft die Berechnung folgendermaßen ab:
und damit ca. 16,7%. Dabei läuft die Berechnung folgendermaßen ab:



Der Ergebnisraum  , welcher zu 1€ Gewinn führt, besteht aus deutlich mehr Elementen. Daher liegt die Wahrscheinlichkeit in diesem Fall auch deutlich höher, nämlich bei
, welcher zu 1€ Gewinn führt, besteht aus deutlich mehr Elementen. Daher liegt die Wahrscheinlichkeit in diesem Fall auch deutlich höher, nämlich bei  bzw. rund 66,7%.
bzw. rund 66,7%.



Die Wahrscheinlichkeit für  errechnet sich analog zum ersten Fall und liegt damit ebenfalls bei
errechnet sich analog zum ersten Fall und liegt damit ebenfalls bei  bzw. ca. 16,7%.
bzw. ca. 16,7%.



Da du nun die Wahrscheinlichkeiten für die einzelnen Ergebnisse weißt, kannst du auch die kumulative Verteilungsfunktion bestimmen. Dazu summierst du die einzelnen Werte schrittweise auf und notierst die Verteilungsfunktion abschnittsweiße.

Auf den ersten Blick scheint diese Schreibweise etwas verwirrend. Wenn wir jedoch 2€ verlieren zu -2€ „gewinnen“ umformulieren, wird das Ganze schon etwas verständlicher. Die Funktion sagt dir also, dass du zu 100% maximal 2 € gewinnen und maximal 2€ verlieren kannst. Die Wahrscheinlichkeit mehr als 2€ zu gewinnen oder zu verlieren ist daher immer gleich 0, da 2€ sowohl den maximalen Gewinn als auch den maximalen Verlust darstellt.
Mit Hilfe dieser Funktion, lässt sich unsere Frage vom Anfang („Mit welcher Wahrscheinlichkeit erhalte ich höchstens 1€?“) nun ganz einfach beantworten. Dazu addierst du die Wahrscheinlichkeit, zwei Nieten zu ziehen (also  ) zu der Wahrscheinlichkeit, genau 1€ zu gewinnen (also
) zu der Wahrscheinlichkeit, genau 1€ zu gewinnen (also  ). Wir machen also mit einer Gesamtwahrscheinlichkeit von
). Wir machen also mit einer Gesamtwahrscheinlichkeit von  83,3% höchstens 1€ Gewinn.
83,3% höchstens 1€ Gewinn.
Bei der Beantwortung solcher Fragen musst du immer genau auf die Formulierung achten. Ist nach der Wahrscheinlichkeit dafür gefragt, genau 1€ zu erhalten, dann musst du nichts zusammenaddieren und kannst als Antwort einfach den Fall, dass ein Gewinnlos gezogen wird, angeben. Das wäre dann also die Wahrscheinlichkeit des schon oben bestimmten Ergebnisraums  , die bei
, die bei  und somit ca. 66,7% liegt.
und somit ca. 66,7% liegt.
Wie man anhand dieser Beispiele sehen kann, ist es im diskreten Fall möglich, zwischen der Wahrscheinlichkeitsfunktion und der Verteilungsfunktion wählen, wenn man Wahrscheinlichkeiten berechnen will.
Empirische Verteilungsfunktion
Ein Sonderfall ist die empirische Verteilungsfunktion. Wie der Name schon vermuten lässt, handelt es sich um empirische, also tatsächlich beobachtete Werte. Daher ist diese auch als Verteilungsfunktion der Stichprobe bekannt.
Formal betrachtet handelt es sich um die Verteilungsfunktion einer diskreten Gleichverteilung
zu den Punkten  . Konkret ordnet die empirische Verteilungsfunktion jedem Wert x den Anteil der Werte der Stichprobe zu, die kleiner oder gleich x sind.
. Konkret ordnet die empirische Verteilungsfunktion jedem Wert x den Anteil der Werte der Stichprobe zu, die kleiner oder gleich x sind.
Folglich werden alle relativen Häufigkeiten summiert, die kleiner oder gleich x sind, wobei das x nicht unbedingt Teil der Stichprobe sein muss.
Verteilungsfunktion Beispiel: diskret
Aber nicht nur für die Wahrscheinlichkeitsverteilung aus dem vorherigen Rechenbeispiel lässt sich eine Verteilungsfunktion bestimmen. Im Folgenden sind einige wichtige diskrete Verteilungen mit ihren dazugehörigen Verteilungsfunktionen aufgelistet.
Verteilungsfunktion Binomialverteilung
Für die Verteilungsfunktion der Binomialverteilung gibt es wie in dem Rechenbeispiel keine wirkliche Formel. Manchmal ist eine Verteilungstabelle gegeben, aus welcher du die kumulierten Wahrscheinlichkeiten ablesen kannst. Ist das nicht der Fall, musst du die Wahrscheinlichkeiten selbst aufaddieren. Wenn du also zum Beispiel wissen möchtest, mit welcher Wahrscheinlichkeit du höchstens zwei Treffer erzielst, musst du die Wahrscheinlichkeiten für 0 Treffer, 1 Treffer und 2 Treffer aufsummieren:

Verteilungsfunktion geometrische Verteilung
Die geometrische Verteilung ist unter anderen auch unter der Bezeichnung „Verteilung des Wartens auf den ersten Erfolg“ bekannt. In diesem Ausdruck spiegelt sich auch schon ihre Grundidee wider. Es handelt sich um ein Bernoulli Experiment mit der Wahrscheinlichkeit p vor und man stellt sich die Frage, wie oft man dieses Experiment ausführen muss, bis der erste Erfolg eintritt. Die dazugehörige Verteilungsfunktion lässt sich deshalb ganz einfach mithilfe der Gegenwahrscheinlichkeit herleiten. Dieses ist nämlich ganz einfach das Produkt der Fehlversuche. Da die Regel gilt, dass die Wahrscheinlichkeit 1 minus die Gegenwahrscheinlichkeit ist, ergibt sich somit folgende Verteilungsfunktion.

Poisson Verteilung Verteilungsfunktion
Für die Verteilungsfunktion der Poisson Verteilung gibt es erneut keine bequeme Formel. Du musst also wieder die einzelnen Werte der Dichtefunktion aufsummieren:

Stetige Verteilungsfunktion
Hat man es mit stetigen Zufallsvariablen zu tun, so kann zur Berechnung von Wahrscheinlichkeiten nur die entsprechende Verteilungsfunktion verwendet werden, welche man durch Integration der Dichtefunktion erhält.
Stetige Verteilungsfunktion zeichnen
Zur Veranschaulichung wird im Folgenden eine einfache Verteilungsfunktion gezeichnet. Es ist dieser Graph einer Dichtefunktion gegeben. Die Wahrscheinlichkeit  entspricht der blau markierten Fläche.
entspricht der blau markierten Fläche.
Man bildet also das Integral von  bis 4 und erhält so den Funktionswert der Verteilungsfunktion an der Stelle
bis 4 und erhält so den Funktionswert der Verteilungsfunktion an der Stelle  . Analog kann so jeder einzelne Punkt der kumulativen Verteilungsfunktion bestimmt werden.
. Analog kann so jeder einzelne Punkt der kumulativen Verteilungsfunktion bestimmt werden.
Stetige Verteilungsfunktion berechnen
Allgemein gilt für Berechnungen mit stetigen Verteilungen, dass es keine Rolle spielt ob die Intervallgrenzen zum Intervall gehören oder nicht. Dies wird anhand folgender Rechenregeln deutlich, welche du auf jeden Fall im Kopf behalten solltest.
1, Es gilt  . Das liegt daran, dass ein einzelner Wert x die Wahrscheinlichkeit von 0 hat.
. Das liegt daran, dass ein einzelner Wert x die Wahrscheinlichkeit von 0 hat.
2, Außerdem gilt für die Wahrscheinlichkeit eines Intervalls  Diese Bedingung musst du beachten, wenn du Wahrscheinlichkeiten berechnen möchtest, welche zwischen zwei Werten liegen.
Diese Bedingung musst du beachten, wenn du Wahrscheinlichkeiten berechnen möchtest, welche zwischen zwei Werten liegen.
3, Man betrachtet das Gegenereignis, wenn man die Wahrscheinlichkeit für > Aussagen berechnen möchte: 
Für unser Rechenbeispiel ist folgende stetige Verteilungsfunktion gegeben:

Gefragt ist nach der Wahrscheinlichkeit, dass X kleiner als 3,5 ist. Um das Ergebnis zu erhalten, setzten wir die Intervallgrenze, also den konkreten Wert in die Verteilungsfunktion ein.



Nun ist die Frage, mit welcher Wahrscheinlichkeit das X zwischen 2,2 und 2,8 liegt. Hier kommt die zweite Rechenregel zur Anwendung. Wir rechnen also:

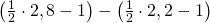


Als letztes wollen wir die Wahrscheinlichkeit berechnen, dass X größer als 3,6 ist. Hier greift die 3.Rechenregel. Wir rechnen also mit der Gegenwahrscheinlichkeit:





Ein weiteres Rechenbeispiel findest du auch in unserem Video zur Dichtefunktion . Dort erfährst du auch, wie du die gesuchten Wahrscheinlichkeiten nicht nur berechnen, sondern die gesuchten Werte aus der Verteilungstabelle ablesen kannst.
Verteilungsfunktion Beispiel: stetig
Wie bereits erwähnt kann zu jeder Wahrscheinlichkeitsverteilung, egal ob diskret oder stetig, eine Verteilungsfunktion gebildet werden. Im Folgenden wird eine Übersicht über die wichtigsten stetigen Verteilungen mit den dazugehörigen Verteilunsfunktionen gegeben.
Verteilungsfunktion Normalverteilung
Die Formel der Verteilungsfunktion der Normalverteilung sieht sehr ungemütlich aus.
Sie summiert alle einzelnen Werte von  bis zum Wert
bis zum Wert  auf und bildet das Integral über die Werte der Dichtefunktion.
auf und bildet das Integral über die Werte der Dichtefunktion.
Aber keine Sorge, da wir es in der Realität mich unendlich vielen stetigen Werten zu tun haben, benutzt man die Verteilungstabelle der Standardnormalverteilung, aus welcher man die gesuchten Wahrscheinlichkeiten nur noch ablesen musst.
Stetige Gleichverteilung Verteilungsfunktion
Die Verteilungsfunktion der stetigen Gleichverteilung gibt man ebenso wie im diskreten Fall aufgeteilt in Abschnitte an:
Verteilungsfunktion Exponentialverteilung
Ebenso wie bei der Dichtefunktion der Exponentailverteilung lassen sich Wahrscheinlichkeiten mit der kumulierten Verteilungsfunktion in diesem Zusammenhang nur für Werte aus dem positiven Bereich berechnen.



