Ziehen mit Zurücklegen
Ziehen mit Zurücklegen von Kugeln aus einer Urne; macht die Reihenfolge einen Unterschied oder nicht? Was passiert, wenn man die Kugeln zurücklegt und so eine Wiederholung des Ergebnisses möglich ist?
Wir bringen Ordnung in das Kugelchaos und erklären dir in unseren Videos alles, was du zu den Urnenmodellen „Ziehen mit Zurücklegen“ und „Ziehen ohne Zurücklegen“ wissen solltest.
Inhaltsübersicht
Stochastik Ziehen mit Zurücklegen
Generell unterscheidet man in der Stochastik zwischen verschiedenen Urnenmodellen. Zum einen musst du unterscheiden zwischen Urnenmodellen mit und ohne Zurücklegen. Zudem spielt es auch eine Rolle ob die Grundgesamtheit oder nur eine Teilmenge betrachtet wird und ob die Reihenfolge der Ergebnisse entscheidend ist oder nicht.
Variation Kombination
So unterscheidet man auch in der Kombinatorik zwischen verschiedenen Szenarien. Betrachtest du Stichproben und nimmst die Reihenfolge als primäres Unterscheidungskriterium des Zufallsexperiment, so kannst du unterscheiden zwischen einer Variation und einer Kombination. Bei Kombinationen spielt die Reihenfolge keine Rolle. Auf zweiter Ebene unterscheidest du dann ob du die Kugel zurücklegst oder nicht. Variationen berücksichtigen die Reihenfolge. Es ist also entscheidend, ob zuerst eine schwarze oder eine weiße Kugel gezogen wird. Auch hier kannst du dann wieder entscheiden, ob die Kugeln nach dem Ziehen wieder in der Kiste landen oder nicht.
Zudem gibt es in der Kombinatorik noch Permutationen . Diese sind einer Variation sehr ähnlich mit dem Unterschied, dass hier nicht nur eine Teilmenge in Form einer Stichprobe betrachtet wird, sondern alle Elemente der Grundgesamtheit.
Im Folgenden behandeln wir alle Varianten von Stichprobenziehungen mit Zurücklegen. Konkret sind das die folgenden beiden Fälle.
- Variation: Betrachtung Stichprobe – mit Zurücklegen mit Reihenfolge
-
Kombination: Betrachtung Stichprobe – mit Zurücklegen ohne Reihenfolge
Die anderen Szenarien erklären wir dir ausführlich in den anderen Videos der Kombinatorik Playlist .
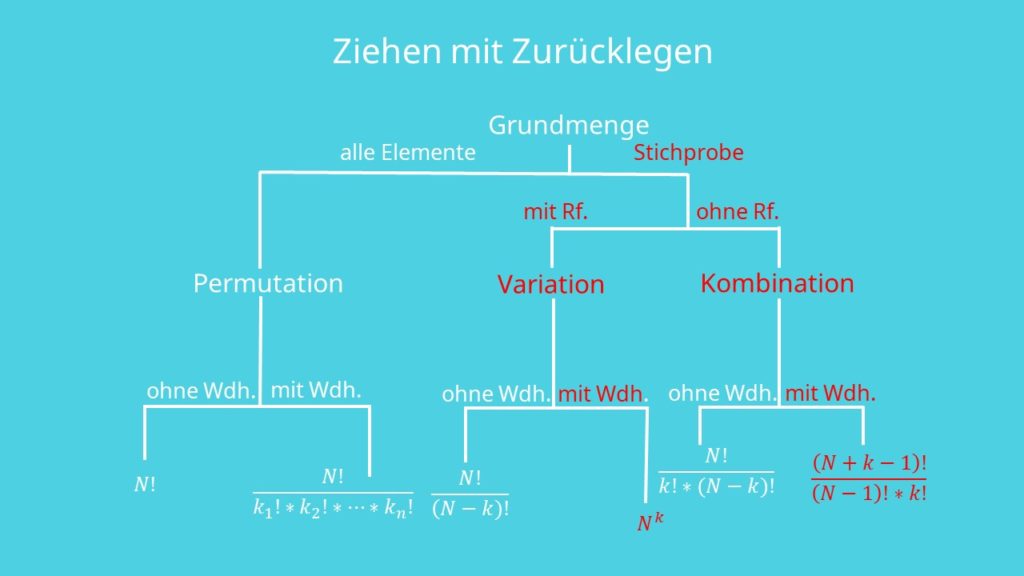
Formel Ziehen mit Zurücklegen
Je nachdem welches Szenario vorliegt, sehen die Formeln zur Berechnung der Anordnungsmöglichkeiten anders aus.
Anstelle von Zurücklegen ist auch oft die Rede von mit und ohne Wiederholung. Lass dich also von diesen Begriffen nicht verwirren.
Ziehen mit Zurücklegen ohne Reihenfolge
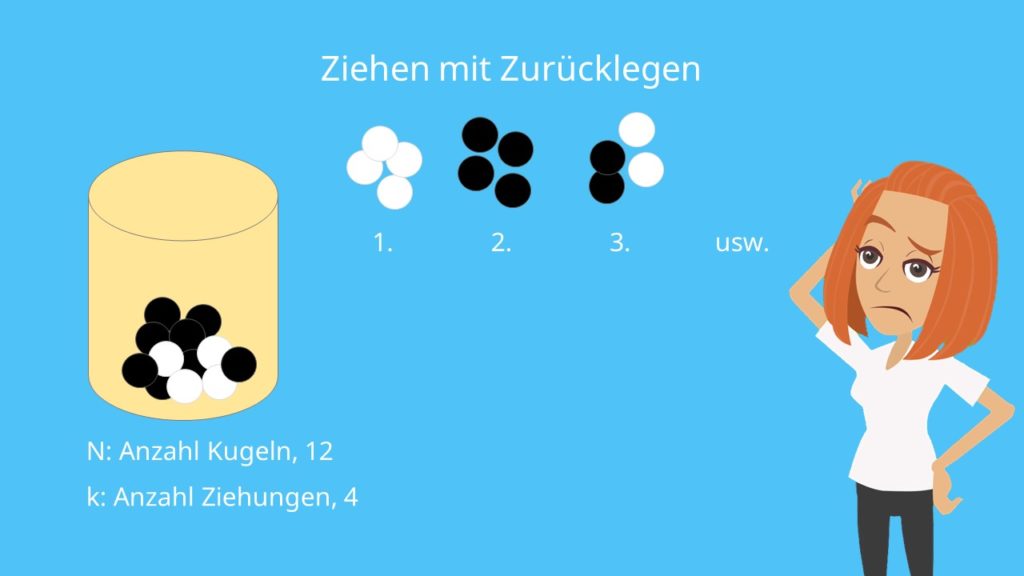
Genau wie bei den Ziehungen ohne Zurücklegen bietet sich das Urnenmodell an, um das Vorgehen verständlich zu erklären. Gehen wir davon aus, dass wir eine Kiste mit 8 schwarzen und 4 weißen Kugeln haben. Wir ziehen daraus wieder, ohne hineinzusehen, 4 Kugeln, nur dass wir sie diesmal nach jedem Zug wieder hineinlegen.
Es befinden sich also nach jedem Zug gleich viele Kugeln in der Urne. Jetzt möchtest du wissen, wie viele mögliche Ergebnisse du bei den 4 Ziehungen erzielen kannst, zum Beispiel nur weiße Kugeln, nur schwarze Kugeln, 2 weiße und 2 schwarze und so weiter. Du hast es also mit einem Urnenmodell mit Zurücklegen ohne Reihenfolge zu tun. Wie du jetzt bereits weißt, spricht wann von Kombinationen, wenn die Reihenfolge keine Rolle spielt.
Wahrscheinlichkeit Ziehen mit Zurücklegen ohne Reihenfolge
Du kannst die Aufgaben zu diesem Szenario des Zufallsexperiments nun mithilfe des Binomialkoeffizienten und der Binomialverteilung lösen.
Um die Anzahl an Möglichkeiten zu berechnen benötigst du eine leicht abgewandelte Form des Binomialkoeffizienten:
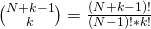
N steht dabei für die Anzahl an Kugeln insgesamt und klein k für die Anzahl an Ziehungen. Wenn wir die gegebenen Werte einsetzen, erhalten wir also:
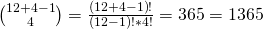
Es gibt also 1365 verschiedene mögliche Ergebnisse.
Als nächstes möchtest du noch die Wahrscheinlichkeit bestimmen, genau eine schwarze Kugel zu ziehen. Dazu musst du wissen, welche Verteilung diesem Zufallsexperiment zugrunde liegt. Bei Ziehungen mit Zurücklegen und ohne Reihenfolge ist das die Binomialverteilung.
Um die Aufgabe zu lösen, benötigst du also die Wahrscheinlichkeitsfunktion der Binomialverteilung. Zur Wiederholung hier noch einmal die Formel:
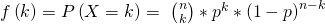
Klein n steht dabei für die Anzahl der Ziehungen. Für die Anzahl an Treffern steht k. Klein p steht für die Wahrscheinlichkeit, eine schwarze Kugel zu ziehen. Da 8 von 12 Kugeln schwarz sind, gilt 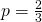 . Da wir nach jedem Zug die Kugel wieder zurück legen bleibt diese Wahrscheinlichkeit immer gleich. Jetzt können wir alle Werte einsetzen:
. Da wir nach jedem Zug die Kugel wieder zurück legen bleibt diese Wahrscheinlichkeit immer gleich. Jetzt können wir alle Werte einsetzen:
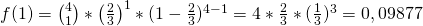
Die Wahrscheinlichkeit genau eine schwarze Kugel zu ziehen liegt also bei ungefähr 9,9.
Zusammenfassend solltest du dir merken, dass Zufallsexperimente mit Ziehungen mit Zurücklegen und ohne Reihenfolge einer Binomialverteilung folgen. Das heißt, du musst die Formeln der Binomialverteilung zur Lösung solcher Aufgaben verwenden.
Ziehen mit Zurücklegen mit Reihenfolge
Aber wie sieht es aus bei Ziehungen mit Zurücklegen mit Reihenfolge? Auch das ist kein Hexenwerk, wenn du weißt welche Formel du bei Ziehungen mit Zurücklegen unter Beachtung der Reihenfolge verwenden musst. Zuerst ist es wichtig, dass du dir erst noch einmal klarmachst, um welches Urnenmodell es sich handelt.
Variation mit Wiederholung
Wir betrachten also Variationen, genauer gesagt Ziehungen mit Zurücklegen, bei denen die Reihenfolge einen Unterschied macht. Ein anschauliches Beispiel hierfür ist der Code eines Fahrradschlosses. Die Reihenfolge der Zahlen machen einen Unterschied, allerdings kann jede Zahl beliebig oft vorkommen.
Wahrscheinlichkeit Ziehen mit Zurücklegen mit Reihenfolge
Gehen wir davon aus, du hast die 5-stellige Kombination deines Fahrradschlosses vergessen. Jede Zahl könnte eine Ziffer zwischen 1 und 6 sein. Wie viele Möglichkeiten kannst du ausprobieren?
Für jede der 5 Stellen der Kombination gibt es 6 Möglichkeiten. Insgesamt gibt es also 6 hoch 5 gleich 7.776 mögliche Kombinationen für das Zahlenschloss.
Allgemein lautet die Formel wie folgt:
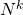
Groß N steht dabei wieder für die Anzahl an Elementen, aus denen gezogen wird, in unserem Fall also die 6 möglichen Ziffern, und klein k steht für die Anzahl der Ziehungen, die in diesem Fall den 5 Stellen der Kombination entsprechen.