Cobb Douglas Produktionsfunktion
Die Cobb Douglas Produktionsfunktion stellt in der Mikroökonomie die Beziehung zwischen den substitutionalen (austauschbaren) Faktoren Arbeit und Kapital auf den Output dar. Die Cobb Douglas Funktion hat folgende Form:
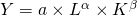
Dabei steht
- Y für die Outputmenge
- K für den Faktoreinsatz Kapital
- L für den Faktoreinsatz Arbeit (Labour)
-
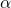 für die Produktionselastizität des Outputs zum Faktor Arbeit
für die Produktionselastizität des Outputs zum Faktor Arbeit -
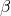 für die Produktionselastizität des Outputs zum Faktor Kapital
für die Produktionselastizität des Outputs zum Faktor Kapital - a für das Effizienzparameter (im Weiteren = 1)
Inhaltsübersicht
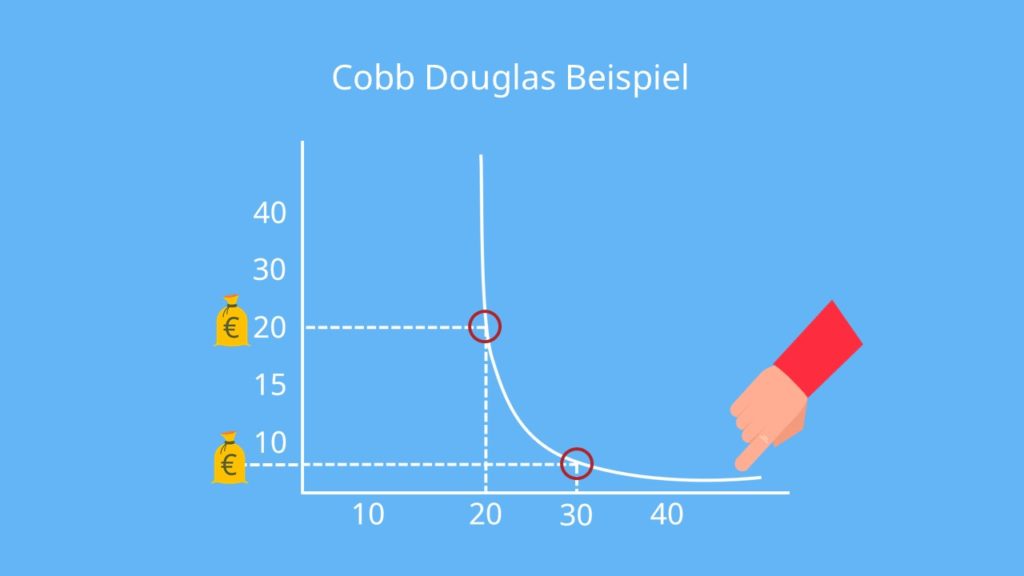
Cobb Douglas Beispiel
Schauen wir uns zunächst ein Beispiel an. Wir gehen hier von einem konstanten Outputniveau 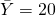 aus, bei einer Produktionsfunktion
von
aus, bei einer Produktionsfunktion
von 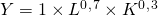 . Dies bedeutet die Produktionsmenge ist fix und die Faktorverteilung wird bestimmt. Dazu setzt man Werte ein, beispielsweise für Arbeit (Mitarbeiter) und enthält entsprechende Werte für Kapital auf der Isoquante.
. Dies bedeutet die Produktionsmenge ist fix und die Faktorverteilung wird bestimmt. Dazu setzt man Werte ein, beispielsweise für Arbeit (Mitarbeiter) und enthält entsprechende Werte für Kapital auf der Isoquante.
Cobb-Douglas-Produktionsfunktion Skalenerträge
Die Parameter 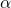 und
und 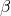 geben Aufschluss über die Art der Skalierung.
geben Aufschluss über die Art der Skalierung.
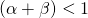 bedeutet abnehmende Skalenerträge
bedeutet abnehmende Skalenerträge
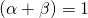 bedeutet konstante Skalenerträge
bedeutet konstante Skalenerträge
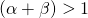 bedeutet zunehmende Skalenerträge
bedeutet zunehmende Skalenerträge
Konstante Skalenerträge führen bei der Produktionsfunktion dazu, dass eine Verdopplung der Einsatzmengen pro Produktionsfaktor ebenfalls die Gesamtproduktion verdoppelt. In diesem Fall wird die Cobb-Douglas-Funktion auch so geschrieben: 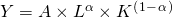 . Bei konstanten Skalenerträgen ist damit eine Substitutionselastizität der Cobb-Douglas-Produktionsfunktion von 1 gegeben.
. Bei konstanten Skalenerträgen ist damit eine Substitutionselastizität der Cobb-Douglas-Produktionsfunktion von 1 gegeben.
Cobb Douglas Produktionsfunktion Isoquanten
Bei der Cobb Douglas Funktion sind die Isoquanten Kurven, die das Faktoraustausch Verhältnis beschreiben vor allem bei imperfekten Substituten wird deshalb eine Cobb Douglas Funktion verwendet. Jedem Outputniveau ist eine eigene Isoquante mit vielen verschiedenen Faktorverteilungen zuzuordnen.
Bei imperfekten Substituten wird häufig eine lineare Produktionsfunktion verwendet, während bei perfekten Komplementen eine Leontief-Produktionsfunktion genutzt wird, welche L-förmig ist.
Cobb Douglas Präferenzen
Da es sich bei Cobb Douglas sowohl um eine Produktionsfunktion als auch um eine Nutzenfunktion handeln kann, analysieren wir noch was die Form über Präferenzen aussagt.
Eine Nutzenfunktion im Allgemeinen gibt Aufschluss über Nutzenniveaus, die in einer Indifferenzkurve abgebildet werden. Diese sind abhängig von den jeweiligen Präferenzen des Individuums. In der Formel der Cobb Douglas Funktion werden diese in den Exponenten α und β abgebildet. Diese geben eine Tendenz welches Gut bevorzugt wird. Dabei zeigt der Exponent mit dem größeren Exponenten an, dass dieses Gut in der Nutzenfunktion höher gewichtet wird. Die Präferenz ist also mit den Exponenten verbunden.
Cobb Douglas Nutzenfunktion
Die Cobb Douglas Funktion ist außerdem eine gängige Nutzenfunktion , deren Grenznutzen und Grenzrate der Substitution zur Berechnung der Nutzenmaximierung verwendet wird.
Meist wird dabei folgende Form verwendet:
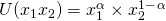
Ableitung Cobb Douglas Funktion
Um wirklich mit der Cobb Douglas Funktion rechnen zu können, ist es wichtig zu verstehen wie die Ableitung funktioniert. Auch innerhalb des Lagrange-Ansatzes wird die Cobb Douglas Nutzenfunktion oft verwendet, dafür ist die Ableitung ein wichtiger Zwischenschritt.
Die Cobb-Douglas Funktion wird partiell abgeleitet, das heißt in unserem Fall einmal nach 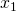 und einmal nach
und einmal nach 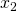 . Bei der Ableitung nach
. Bei der Ableitung nach 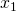 wird
wird 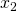 als Konstante behandelt. Schauen wir uns einmal den Fall an für
als Konstante behandelt. Schauen wir uns einmal den Fall an für 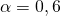 und
und 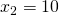
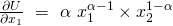
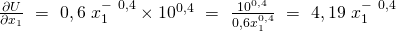
Diese Ableitung ist die Grenzrate der Substitution. Für die partielle Ableitung nach 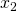 schaut die Formel so aus:
schaut die Formel so aus:
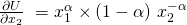
Die Ableitung der Cobb Douglas ist ein wichtiger Rechenschritt, der in vielen Rechenbeispielen der Volkswirtschaft gebraucht wird.